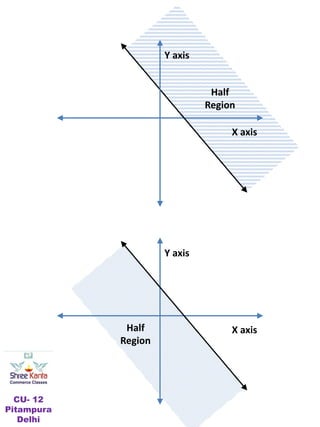
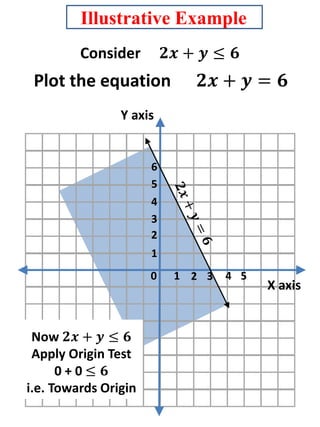
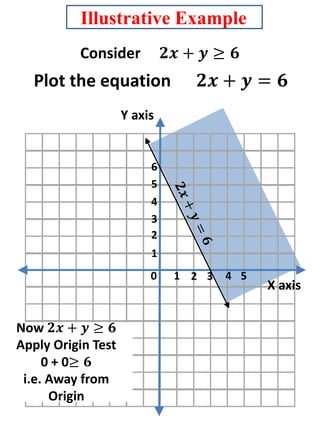
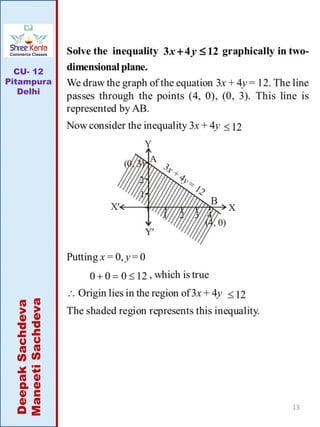
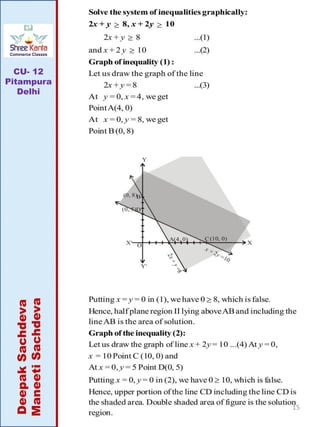
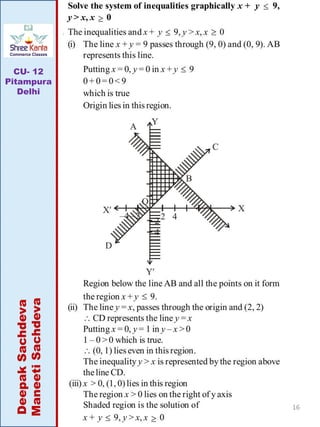
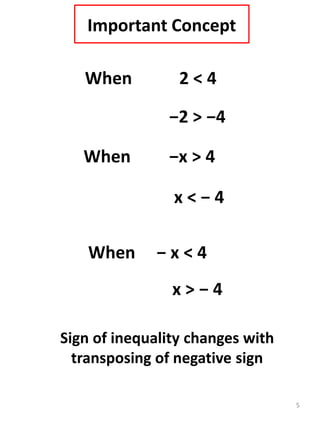This document discusses linear inequalities. It defines an inequality as any statement involving the symbols >, <, ≤ or ≥. A linear inequality relates two linear polynomials with a sign of inequality. There are numerical inequalities that do not involve variables and literal inequalities that do involve variables. Linear inequalities can contain one or more variables. Inequalities with > or < are strict, while those with ≥ or ≤ are slack or non-strict. The solution set of a linear inequality in one variable can be represented on a number line using open or closed circles. A linear inequality containing ≥ or ≤ is represented geometrically by a half-plane on either side of the corresponding linear equation.

1. Linear
In-equations
1
CU- 12
Pitampura
Delhi

2. Concept Building
2
INEQUALITY
Any statement involving the symbols
>, < , ≤ or ≥ is called an inequality.
Two linear polynomials is related by a
sign of inequality viz, >, <, ≥ or ≤ is called
a linear inequality.
Types of Inequalities
(i) Inequalities which do not involve
variables are called numerical
inequalities. e.g 3<8, 5>2
(ii) Inequalities which involve variables
are called literal inequalities.
e.g. x > 3, y ≤ 5
(i) An inequality may contain more
than one variable and it can be
linear, quadratic or cubic etc.
(ii) Inequalities involving the symbol >
or < are called strict inequalities.
(iii) Inequalities involving the symbol ≥
or ≤ are called slack inequalities.
CU- 12
Pitampura
Delhi

3. 3
Representation of Solution of Linear Inequality
in One Variable on a Number Line
(i) If the inequality involves ≥ or ≤ , we
draw filled circle (•) on the number line
to indicate that the number
corresponding to the filled circle is
included in the solution set.
e.g. x ≤ 5 𝒊. 𝒆. 𝒙 𝝐 (−∞, 𝟓]
5 ∞
−∞
x ≥ 5 𝒊. 𝒆. 𝒙 𝝐 [𝟓, ∞)
5 ∞
−∞

4. 4
(ii) If the inequality involves > or <, we
draw an open circle (○) on the number
line to indicate that the number
corresponding to the open circle is
excluded from the solution set.
5 ∞
−∞
x > 5 𝑖. 𝑒. 𝒙 𝝐 (𝟓, ∞)
5 ∞
−∞
x < 𝟓 𝒊. 𝒆. 𝒙 𝝐 (−∞, 𝟓)

5. 5
Important Concept
When 2 < 4
−2 > −4
When −x > 4
x < − 4
When − x < 4
x > − 4
Sign of inequality changes with
transposing of negative sign

6. 6
Examples
CU- 12
Pitampura
Delhi

7. 7
CU- 12
Pitampura
Delhi

8. Graph of a linear Inequality
A linear inequality containing the sign ≥
𝒐𝒓 ≤ is represented by a half plane either
side of the line, represented by the linear
equation corresponding to the given linear
equality.
CU- 12
Pitampura
Delhi

9. X axis
Y axis
Half
Region
X axis
Y axis
Half
Region
CU- 12
Pitampura
Delhi

10. Illustrative Example
Consider 𝟐𝒙 + 𝒚 ≤ 𝟔
Plot the equation 𝟐𝒙 + 𝒚 = 𝟔
Y axis
X axis
0 1 2 3 4 5
1
2
3
4
5
6
Now 𝟐𝒙 + 𝒚 ≤ 𝟔
Apply Origin Test
0 + 0 ≤ 𝟔
i.e. Towards Origin

11. Illustrative Example
Consider 𝟐𝒙 + 𝒚 ≥ 𝟔
Plot the equation 𝟐𝒙 + 𝒚 = 𝟔
Y axis
X axis
0 1 2 3 4 5
1
2
3
4
5
6
Now 𝟐𝒙 + 𝒚 ≥ 𝟔
Apply Origin Test
0 + 0≥ 𝟔
i.e. Away from
Origin

12. 12
CU- 12
Pitampura
Delhi

13. 13
CU- 12
Pitampura
Delhi

14. 14
CU- 12
Pitampura
Delhi

15. 15
CU- 12
Pitampura
Delhi

16. 16
CU- 12
Pitampura
Delhi

17. 17
CU- 12
Pitampura
Delhi