Ibisml2011 06-20

2011年6月20日第五回情報論的学習理論と機械学習研究会 (IBISML)

ウェーブレット木による
バイナリコードの高速検索
田部井靖生, 津田宏治
科学技術振興機構, 産業技術総合研究所

1

発表の流れ
• 背景
近傍検索法の必要性
• 本発表で用いるデータ構造
ウェーブレット木
• バイナリコードの検索(提案法)
幾何制約を取り入れたウェーブレット
木による検索

• 実験
既存手法との比較 (転置インデックス)
8000万画像
2

ε-近傍検索
• クエリデータ点の距離ε以内の点をデータ
ベースから検索する
入力: n データベース点 {xi }n
i=1
d ,

クエリデータ点 xq d
, 距離閾値ε

出力:クエリデータ点 xq から距離ε以内の
データベース点

3

近傍検索の必要性
• あらゆる手法のもととなるタスク
例) semi-supervised learning, spectral
clustering, ROI detection in images, etc

• ２つの研究の方向性
1. 空間分割による索引に基づく検索法
cover tree(ICML,06), spill tree(NIPS05) etc
高次元データに対しては有効ではない(NIPS,09)
2. locality sensitive codeを用いた検索法
コンパクトにデータを保持することが可能
エラーと速度のトレードオフをコントロールす
ることが困難

4

手法の概要
• 幾何制約を取り入れたlocality sensitive
codeの高速検索
エラー制御
Shift-invariant kernel based hashing (NIPS,09)

• ウェーブレット木(SODA,03)による索引
two dimensional range searchに幾何制約を取り入
れる
探索空間の枝刈り

5

発表の流れ
• 背景
• バイナリコードの検索法(提案法)
幾何制約を取り入れたウェーブレッ
ト木による検索
• 実験
8000万画像

6

ウェーブレット木 (SODA,03)
• 整数配列のself-index
A 1 3 6 8 2 5 7 1 2 7 4 5

• 高速な配列上の操作
連続した区間内の値cの出現回数
値cのi番目の出現位置
連続した区間内の最大値,最小値,k番目に大きい値,
出現位置 etc

• 区間の長さに関して定数時間, 約nlogsビット
のメモリ(n:配列長,s:整数の最大値)

• 2次元Arange intersection:
ms の範囲内で, n個の区間で共通す
mi t

る要素を求める
7

配列上のRange Intersection
• 長さNの配列 A, 1 Ai M
i j k "
A 1 3 6 8 2 5 7 1 2 7 4 5

• Range Intersection: rint(A,[i,j],[k,l])
A[i,j]とA[k,l]の共通要素を求める
ナイーブ法=２つの区間を連結してソート

• 配列のインデックス(ウェーブレット木)を使
い, 高速に解く

8

部分配列上の木:
下半分:左の子上半分:右の子
[1,8]
1 3 6 8 2 5 7 1 7 2 4 5

[1,4] [5,8]
1 3 2 1 2 4 6 8 5 7 7 5

[1,2] [3,4] [5,6] [7,8]
1 2 1 2 3 4 6 5 5 8 7 7

1 1 2 2 3 4 5 5 6 7 7 8

9

それぞれの要素が下半分(0)
または上半分(1)かを記憶
[1,8]
0 0 1 1 0 1 1 0 1 0 0 1

[1,4] [5,8]
0 1 0 0 0 1 0 1 0 1 1 0

[1,2] [3,4] [5,6] [7,8]
0 1 0 1 0 1 1 0 0 1 0 0

1 2 3 4 5 6 7 8
10

ランク辞書によりビット
配列をインデックス
• 定数時間でランク操作が可能
rankc (B, i) : B[1..i] のc {0, 1} の個数を返す

• 代表的な手法: rank9sel (Vigna,08)
✴ 例) B=0110011100
i 1 2 3 4 5 6 7 8 9 10
rank1 (B, 8) = 5 011001110 0
rank0 (B, 5) = 3 011001110 0

11

ランク辞書の実装
• 長さnのビット配列 B を
長さ
B
= log2 n
の大ブロックに
分割
RL
RL:大ブロックの１の個数

RS
• R のそれぞれのブロック
L

を長さ s = log2 n/2 の小ブ
ロックに分割
Rs:小ブロックの1の個数
rank1 (B, i) = RL [i/ ] + Rs [i/s] + (remaining rank)

• 時間:O(1) メモリ:n+o(n) bits
12

区間の定数時間分割
• ランク操作により, 区間の分割は定数時
間で行うことができる
左の子: rank0, 右の子: rank1
• ナイーブ法: 全区間の要素の総和に線形時間
[1,8]
Aroot 1 3 6 8 2 5 7 1 7 2 4 5

rank0 rank1
[1,4] [5,8]
Aleft 1 3 2 1 2 4 Aright 6 8 5 7 7 5

13

枝刈りによるrange intersection
の高速計算

Pruned [1,8]
1 3 6 8 2 5 7 1 7 2 4 5

[1,4] [5,8]
1 3 2 1 2 4 6 8 5 7 7 5

[1,2] [3,4] [5,6] [6,8]
1 2 1 2 3 4 6 5 5 8 7 7

1 1 2 2 3 4 5 5 6 7 7 8

solution!!

14

Two dimensional range
intersection
• 長さNの配列 A, 1 Ai M
i j k "
A 1 3 6 8 2 5 7 1 2 7 4 5

• Two dimensional range intersection:
trint(A,[i,j],[k,l],[ms,mt])
A[i,j]とA[k,l]の共通要素をms Ai mtの範囲内
で求める
探索空間の枝刈りが可能

15

Two dimensional range
intersection
2 A[i] 3
Pruned// [1,8]
1 3 6 8 2 5 7 1 7 2 4 5

[1,4] [5,8]
1 3 2 1 2 4 6 8 5 7 7 5

[1,2] [3,4] [5,6] [6,8]
1 2 1 2 3 4 6 5 5 8 7 7

1 1 2 2 3 4 5 5 6 7 7 8

solu3on!!/

16

発表の流れ
• 背景
幾何制約を取り入れたウェーブレッ
ト木による検索
• 実験
8000万画像

17

バイナリコードの類似度検索
xi=(1.2,-0.9,2,3,4,...) • ベクトルデータ
Xi=100011... • バイナリコード(SIHK)
10 00 11... • ブロック分割
1-10, 2-00, 3-11,... • Bag-of-words表現
• Semi-conjunctive query
クエリQに対して, 少なくともkワードを共有す
るデータXiをデータベースからすべて求める
|Xi Q| k
18

Shift-invariant kernel based hashing (NIPS,09)

• ベクトルデータ x d
をバイナリs {0, 1}へ射影
s = sign(cos(r x + ) + )
T

r d
N (0, )
:正規分布からのランダムベクトル
, : 一様分布U[-1,1], U[0,2π]からの乱数

• 2つのベルトルx,yの (x) = 2 cos(rT x + ) の内積の期
待値 Er, [ (x) (y)] がtransition invariant kernel
k(x,y)=k(x-y)の近似(Rahimi and Recht,07)

• L回繰り返してバイナリコード(文字列)へ射影
• 元の空間のユーグリッド距離を文字列のハミン
グ距離で保つ
• データのコンパクトな表現
19

転置インデックス,配列,ウェーブレット木
ワード識別子 • データベースを転置インデック
1-00 1,3,6,8 に格納
1-01 2,5,7 • すべての行を連結し, 配列に格納
1-10 2,7 • ウェーブレット木により
1-11 4,5 配列を索引付ける
2-00 2,6,8
• Semi-conjunctive query
= Extension of range
intersection
A 1 3 6 8 2 5 7 2 7 4 5 26 8
6
配列中少なくともk回現れる
識別子を発見する
20

幾何制約
• クエリーｑに対して, 距離ε
以内の点は, 第一主成分の座
h6 標hiもε以内
q h4 h5
ε is = min{i|hq hi }
ie = min{i|hi hq + }
h3
hq
h2
h1 • is i ieかつ |Xi Q| k
を満たすiをすべて求める
hq hi hq + (Extension of two
dimensional range
intersecion)
21

2種類のエラー
• I*:クエリqに対して, 距離ε以内の
データベース中の点xiの集合
I = {i| (xi , q) , is i ie }
• I: クエリQに対して, k個のワードを共有
するデータベース中の点Xiの集合
I = {i||Xi Q| k, is i ie }

• False positive rate: Fp = |I I |/|I|
• False negative rate: Fn = |I I|/|I |

22

False negative rateの上限
• False negative rateは以下のように抑え
ることができる
b
Fn 1 p0 (1
k
p0 )
b k
p0 = (1 p)
k=0

• pは近傍に対する非衝突確率の上限
8 1 exp( 2
/2)
p= 2
m=0
4m2 1

• False negative rateをできるだけ小さく
するようにパラメータを決定できる

23

時間とメモリ
• クエリあたりの検索時間: O(τb)
τ:たどったノード数
b:ブロックの個数(L/l)

• メモリ:(1+α)Nlogn+MlogN ビット
N: すべてのワードの個数
M:配列中の最大整数
n:データ点の数

• 転置インデックスのメモリ:Nlognビット
• 転置インデックスと比較して約60%のオー
バーヘッド
24

発表の流れ
• 背景
幾何制約を取り入れたウェーブレット
木による検索

• 実験
既存手法との比較 (転置インデックス)
8000万画像
25

実験
• Tiny image dataset (Torralba et al., 08)
約8000万データ, 386次元
• 500万データを用いて, 従来法 (転置インデックス)
と比較
コード長 L=128,256,1024ビット
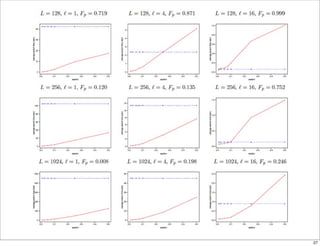
ブロック長 =1,4,16
距離の閾値ε 0.01,から0.5の値
ブロックマッチの個数の閾値kは, false
negative rateの上限が0.001にできるだけ近く
なるように決める

• false negative rate一定のもとで, false positive
rateと速度の変化をみる
26

コード長L=256, ブロック長=4,
距離の閾値ε=0.1の検索時間

202秒

７秒

28

構築時間

４h

30

まとめ
• 高速かつメモリー効率の良いバイナリ
コードの検索法
• 第一主成分による制約を入れてsemi-
conjunctive queryを効率的に解く

• ウェーブレット木による索引
• バイナリコードへの変換は
shift-invariant kernel based hashing
を用いる
• 8000万画像にも適応可能
31

Ibisml2011 06-20

More Related Content

What's hot

Viewers also liked

Similar to Ibisml2011 06-20

Recently uploaded

Ibisml2011 06-20