The document discusses the distributive property in mathematics. It provides examples of using the distributive property to evaluate numerical expressions and rewrite algebraic expressions. It also gives a step-by-step example of using the distributive property to find the total cost of baseball helmets when the price per helmet is given. The distributive property allows numbers and symbols to represent mathematical ideas by distributing a number across terms within parentheses during multiplication.

1. Name the property shown by each statement.
1. a + (b + c) = (a + b) + c 2. 3(ab) = (ab)3
3. z + y + 0 = z + y 4. 7 • h • 0 = 0
5. Dance lessons cost $100 per couple per half hour.
Assume 3 couples want to take dance lessons for an
hour. Use mental math to find the total cost of the dance
lessons for the couples.
Course 2, Lesson 5-4

2. Answers
1. Associative (+)
2. Commutative (x)
3. Identity (+)
4. Multiplicative (0)
5. $600
Course 2, Lesson 5-4

3. HOW can you use numbers and
symbols to represent mathematical
ideas?
Expressions and Equations
Course 2, Lesson 5-4

4. • 7.EE.1
Apply properties of operations as strategies to add, subtract, factor,
and expand linear expressions with rational coefficients.
• 7.EE.2
Understand that rewriting an expression in different forms in a
problem context can shed light on the problem and how the
quantities
in it are related.
Course 2, Lesson 5-4 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

5. Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
5 Use appropriate tools strategically.
7 Look for and make use of structure.
Course 2, Lesson 5-4 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

6. • To model the Distributive Property
using algebra tiles
• To use the Distributive Property to
evaluate numerical expressions
Course 2, Lesson 5-4
Expressions and Equations

7. Course 2, Lesson 5-4
Expressions and Equations
• Distributive Property
• equivalent expressions

8. Course 2, Lesson 5-4
Expressions and Equations
Words The Distributive Property states that to multiply a sum or
difference by a number, multiply each term inside the
parenthesis by the number outside the parenthesis.
Symbols a(b + c) = ab + ac a(b – c) = ab – ac
Examples 4(6 + 2) = 4 • 6 + 4 • 2 3(7 – 5) = 3 • 7 – 3 • 5

9. 1
Need Another Example?
2
Step-by-Step Example
1. Use the Distributive Property to evaluate 8(–9 + 4).
Expand using the Distributive Property.
Multiply. Then add.
8(–9 + 4) = 8(–9) + 8(4)
= –72 + 32 or –40

10. Answer
Need Another Example?
Use the Distributive Property to evaluate
7(3 + 12)
7 • 3 + 7 • 12; 105

11. 1
Need Another Example?
2
Step-by-Step Example
2. Use the Distributive Property to rewrite 4(x + 7).
Expand using the Distributive Property.
Simplify.
4(x + 7) = 4(x) + 4(7)
= 4x + 28

12. Answer
Need Another Example?
Use the Distributive Property to rewrite
11(x + 5).
11x + 55

13. 1
Need Another Example?
2
3
4
Step-by-Step Example
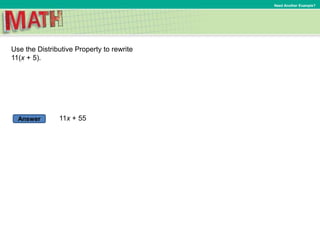
3. Use the Distributive Property to rewrite 6(p – 5).
Rewrite p – 5 as p + (–5).
Expand using the Distributive Property.
6(p – 5) = 6[p + (–5)]
= 6(p) + 6(–5)
Simplify.= 6p + (–30)
Definition of subtraction= 6p – 30

14. Answer
Need Another Example?
Use the Distributive Property to rewrite
5(p – 8).
5p – 40

15. 1
Need Another Example?
2
3
Step-by-Step Example
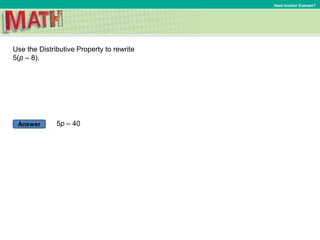
4. Use the Distributive Property to rewrite –2(x – 8).
Rewrite x – 8 as x + (–8).
Expand using the Distributive Property.
–2(x – 8) = –2[x + (–8)]
= –2(x) + –2(–8)
Simplify.= –2x + 16

16. Answer
Need Another Example?
Use the Distributive Property to rewrite
–3(x – 2).
–3x + 6

17. 1
Need Another Example?
2
Step-by-Step Example
5. Use the Distributive Property to rewrite 5(–3x + 7y).
Expand using the Distributive Property.
Simplify.
5(–3x + 7y) = 5(–3x) + 5(7y)
= –15x + 35y

18. Answer
Need Another Example?
Use the Distributive Property to rewrite
4(–9x + 1).
–36x + 4

19. 1
Need Another Example?
2
3
4
Step-by-Step Example
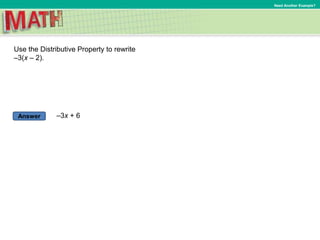
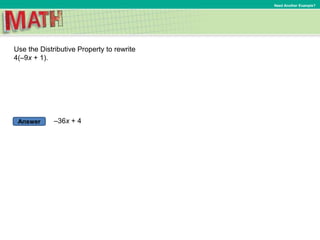
6. Use the Distributive Property to rewrite (x – 6).
Rewrite x – 6 as x + (–6).
Expand using the Distributive Property.
(x – 6) = [x + (–6)]
= x + (–2) Simplify.
= x – 2 Definition of subtraction

20. Answer
Need Another Example?
Use the Distributive Property to rewrite
(x – 16).

21. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
7. Mr. Ito needs to buy batting helmets for the baseball
team. The helmets he plans to buy are $19.95 each.
Find the total cost if Mr. Ito needs to buy 9 batting
helmets for the team.
Distributive Property
Multiply.
Rename $19.95 as $20.00 – $0.05. Then use the Distributive
Property to find the total cost mentally.
= $180 – $0.45
Subtract.= $179.55
= 9($20.00) – 9($0.05)9($20.00 – $0.05)
The total cost of the helmets is $179.55.

22. Answer
Need Another Example?
Fifteen students are buying T-shirts that cost
$10.60 each. Use the Distributive Property to
find the total cost of the shirts.
$159; 15($10 + $0.60)
= 15 • 10 + 15 • 0.6 = 150 + 9, or 159

23. How did what you learned
today help you answer the
HOW can you use numbers and symbols
to represent mathematical ideas?
Course 2, Lesson 5-4
Expressions and Equations

24. How did what you learned
today help you answer the
HOW can you use numbers and symbols
to represent mathematical ideas?
Course 2, Lesson 5-4
Expressions and Equations
Sample answers:
• By using the Distributive Property to evaluate
numerical expressions
• By using the Distributive Property to rewrite algebraic
expressions
• By using the Distributive Property to solve real-world
problems

25. Explain how today’s lesson
on the Distributive Property
will help you with simplifying
algebraic expressions.
Ratios and Proportional RelationshipsExpressions and Equations
Course 2, Lesson 5-4
dnpickens7@yahoo.com