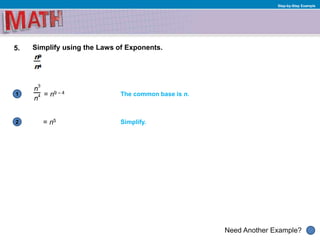
1) The document provides examples of writing expressions using exponents and evaluating those expressions. It gives the expressions 2c8, 85, and m5n3p3 as examples and evaluates the expressions 512, 216, and m5n3p3. 2) It then discusses rules for multiplying and dividing powers with the same base: to multiply powers with the same base, add the exponents, and to divide powers with the same base, subtract the exponents. 3) Several step-by-step examples demonstrate simplifying expressions using these rules to multiply and divide exponents.

1. Course 3, Lesson 1-3
Write each expression using exponents.
1.
2.
3.
Evaluate each expression.
4.
5.
6. Write
using exponents.
• • • • • • • •c c c c c c c c c
8 • 8 • 8 • 8 • 8
1 1
2 2
• • • • x • • • • • •x y x y x x x y
9
2
3
6
• • • • • • • • • •m n m p m n m p n m p

2. Course 3, Lesson 1-3
ANSWERS
1. c9
2. 85
3.
4. 512
5. 216
6. m5n3p3
 
 
 
2
6 31
2
x y

3. WHY is it helpful to write numbers in
different ways?
The Number System
Course 3, Lesson 1-3

4. Course 3, Lesson 1-3 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council of
Chief State School Officers. All rights reserved.
The Number System
• 8.EE.1
Know and apply the properties of integer exponents to generate
equivalent numerical expressions.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
7 Look for and make use of structure.

5. • To multiply and divide powers
Course 3, Lesson 1-3
The Number System

6. • monomial
Course 3, Lesson 1-3
The Number System

7. Course 3, Lesson 1-3
The Number System
Words To multiply powers with the same base, add their
exponents.
Numbers Algebra
Examples or4 3 4 3
2 2 2 
 7
2 m n m n
a a a 


8. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Simplify using the Laws of Exponents.
52 • 5
52 • 5 = 52 • 51 5 = 51
The common base is 5.= 52 + 1
= 53 or 125 Add the exponents.
Simplify.
Check 52 • 5 = (5 • 5) • 5
= 5 • 5 • 5
= 53

9. Answer
Need Another Example?
Simplify 76 • 7 using the Laws of Exponents.
77

10. 1
Need Another Example?
2
Step-by-Step Example
2. Simplify using the Laws of Exponents.
c3 • c5
c3 • c5 = c3 + 5 The common base is c.
Add the exponents.= c8

11. Answer
Need Another Example?
Simplify r4 • r6 using the Laws of Exponents.
r10

12. 1
Need Another Example?
2
3
Step-by-Step Example
3. Simplify using the Laws of Exponents.
–3x2 • 4x5
–3x2 • 4x5 = (–3 • 4)( x2 • x5) Commutative and Associative Properties
The common base is x.= (–12)(x2 + 5)
= –12x7 Add the exponents.

13. Answer
Need Another Example?
Simplify −7x2 • 11x4 using the Laws of
Exponents.
−77x6

14. Course 3, Lesson 1-3
The Number System
Words To divide powers with the same base, subtract their
exponents.
Numbers Algebra
Examples
or
7
7 3
3
3
3
3

 4
3 , where 0
m
m n
n
a
a a
a

 

15. 1
Need Another Example?
2
Step-by-Step Example
4. Simplify using the Laws of Exponents.
= 48 – 2 The common base is 4.
Simplify.= 46 or 4,096

16. Answer
Need Another Example?
Simplify using the Laws of Exponents.
610

17. 1
Need Another Example?
2
Step-by-Step Example
5. Simplify using the Laws of Exponents.
= n9 – 4 The common base is n.
Simplify.= n5

18. Answer
Need Another Example?
Simplify using the Laws of Exponents.
a6

19. 1
Need Another Example?
2
3
4
Step-by-Step Example
6. Simplify using the Laws of Exponents.
= Group by common base.
Subtract the exponents.= 23 • 31 • 51
23 = 8= 8 • 3 • 5
Simplify.= 120

20. Answer
Need Another Example?
Simplify .
450

21. 1
Need Another Example?
2
3
Step-by-Step Example
7. Hawaii’s total shoreline is about 210 miles long.
New Hampshire’s shoreline is about 27 miles long.
About how many times longer is Hawaii’s shoreline
than New Hampshire’s?
To find how many times longer, divide 210 by 27.
Quotient of Powers= 210 – 7 or 23
Hawaii’s shoreline is about 23 or 8 times longer.

22. Answer
Need Another Example?
One centimeter is equal to 10 millimeters, and
one kilometer is equal to 106 millimeters. How
many centimeters are in one kilometer?
105 cm

23. How did what you learned
today help you answer the
WHY is it helpful to write numbers in
different ways?
Course 3, Lesson 1-3
The Number System

24. How did what you learned
today help you answer the
WHY is it helpful to write numbers in
different ways?
Course 3, Lesson 1-3
The Number System
Sample answer:
• If you need to multiply or divide large numbers that can
be written with the same base(s), it is easier to do when
the numbers are written in exponential form.

25. Explain how to
evaluate exponents
when multiplying and
dividing numbers with
the same base in
exponential form.
Ratios and Proportional RelationshipsThe Number System
Course 3, Lesson 1-3