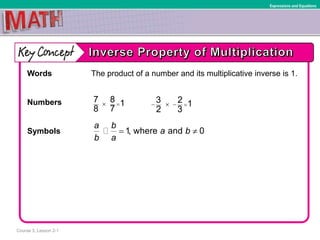
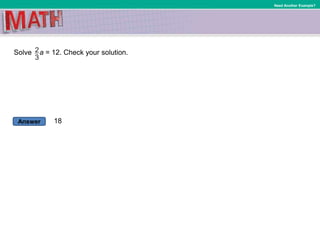
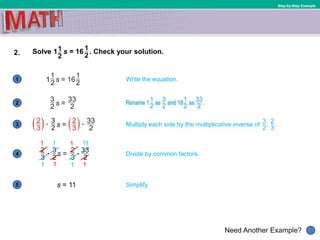
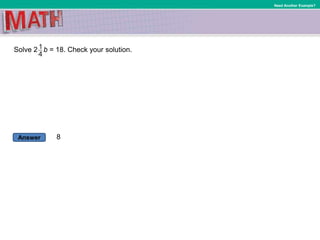
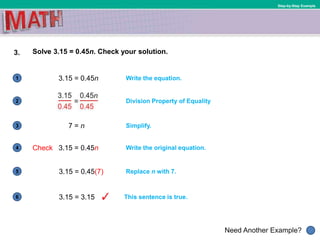
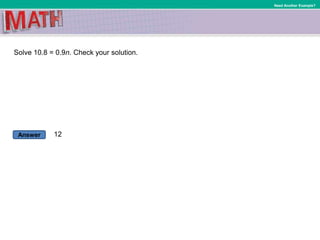
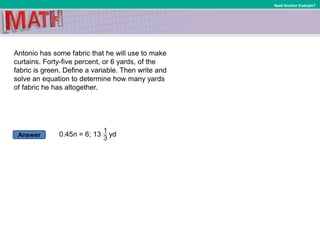
This document provides instruction on solving linear equations with one variable. It begins by defining key terms like multiplicative inverse and coefficient. It then provides examples of solving various equations by multiplying or dividing both sides of the equation by the same term to isolate the variable. These examples include equations with fractions, decimals, and percentages. The document emphasizes using the inverse operation property to solve equations and checking solutions. It aims to help students solve equations that may require expanding and combining like terms.

1. Course 3, Lesson 2-1
Name all sets of numbers to which each real number
belongs.
1. 286
2.
Replace each with <, >, or = to make a true
statement.
3. 5.9
4. 120%
5. Are irrational numbers always, sometimes, or never
rational numbers?
6. Name one set of numbers to which does NOT
belong.
15
34
2
3

1
1
5

2. Course 3, Lesson 2-1
ANSWERS
1. rational, integer, whole, real, natural
2. irrational, real
3. <
4. =
5. never
6. Sample answer: negative integers

3. WHAT is equivalence?
Expressions and Equations
Course 3, Lesson 2-1

4. • 8.EE.7
Solve linear equations in one variable.
• 8.EE.7a
Give examples of linear equations in one variable with one solution,
infinitely many solutions, or no solutions. Show which of these
possibilities is the case by successively transforming the given equation
into simpler forms, until an equivalent equation of the form x = a, a = a,
or a = b results (where a and b are different numbers).
Course 3, Lesson 2-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council
of Chief State School Officers. All rights reserved.
Expressions and Equations

5. • 8.EE.7b
Solve linear equations with rational number coefficients, including
equations whose solutions require expanding expressions using the
distributive property and collecting like terms.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
7 Look for and make use of structure.
Course 3, Lesson 2-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council
of Chief State School Officers. All rights reserved.
Expressions and Equations

6. To
• solve equations using the Inverse
Property of Multiplication
• solve equations with rational coefficients
Course 3, Lesson 2-1
Expressions and Equations

7. • multiplicative inverse
• coefficient
Course 3, Lesson 2-1
Expressions and Equations

8. Course 3, Lesson 2-1
Expressions and Equations
Words The product of a number and its multiplicative inverse is 1.
Numbers
Symbols
7 8 1
78
 3 2 1
2 3
 
1, where and 0
a b
a b
b a
 

9. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
1. Solve c = 18. Check your solution.
7
8
c = 18
c = 18
c = 24
Check c = 18
(24) = 18
18 = 18
Write the equation.
Multiply each side by the multiplicative inverse of , .
Write 18 as . Divide by common factors.
Simplify.
Write the original equation.
Replace c with 24.
Write 24 as . Divide by common factors.
611
1 1 1
?
6
1
This sentence is true.

10. Answer
Need Another Example?
18
Solve a = 12. Check your solution.

11. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
2. Solve 1 s = 16 . Check your solution.
s = 11
Write the equation.
Simplify.
Multiply each side by the multiplicative inverse of , .
Divide by common factors.
11 111
11 11

12. Answer
Need Another Example?
Solve 2 b = 18. Check your solution.
8

13. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
3. Solve 3.15 = 0.45n. Check your solution.
3.15 = 0.45(7)
Write the equation.
Replace n with 7.
Division Property of Equality
Simplify.
3.15 = 0.45n
7 = n
Check 3.15 = 0.45n Write the original equation.
3.15 = 3.15 This sentence is true.

14. Answer
Need Another Example?
Solve 10.8 = 0.9n. Check your solution.
12

15. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
4. Latoya’s softball team won 75%, or 18, of its games.
Define a variable. Then write and solve an equation to
determine the number of games the team played.
n = 24 Simplify.
Write the equation. Write 75% as 0.75.
Division Property of Equality
Latoya’s softball team won 18 games, which was 75% of the
games played. Let n represent the number of games played.
Write and solve an equation.
0.75n = 18
Latoya’s softball team played 24 games.

16. Answer
Need Another Example?
Antonio has some fabric that he will use to make
curtains. Forty-five percent, or 6 yards, of the
fabric is green. Define a variable. Then write and
solve an equation to determine how many yards
of fabric he has altogether.
0.45n = 6; 13 yd

17. How did what you learned
today help you answer the
WHAT is equivalence?
Course 3, Lesson 2-1
Expressions and Equations

18. How did what you learned
today help you answer the
WHAT is equivalence?
Course 3, Lesson 2-1
Expressions and Equations
Sample answers:
• Two sides of an equation remain equal if you multiply
both sides of the equation by the same fraction or
decimal.
• Two sides of an equation remain equal if you divide
both sides of the equation by the same decimal.

19. Describe the first step
to solve the equation below:
− y = 2.5
Ratios and Proportional RelationshipsExpressions and Equations
1
3
Course 3, Lesson 2-1