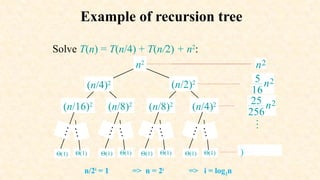
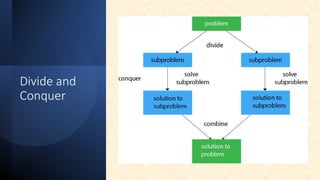
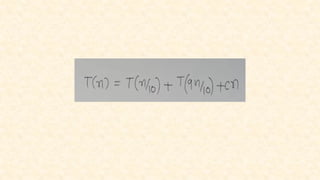The document outlines concepts related to the mathematical analysis of recursive techniques in algorithms, particularly focusing on recurrence relations that express algorithm running times. It describes methods for solving these recurrences including iteration, substitution, recursion tree, and master theorem, accompanied by examples. Key recursive algorithms such as binary search are also analyzed to illustrate the application of these concepts.

1. Course Name: Design and Analysis of Algorithm
Topic: : Mathematical Analysis of Recursive techniques
Course code : CS 3102
Credits : 4
Mode of delivery : Hybrid (Power point presentation)
Faculty : Dr. Ajit Noonia
Email-id : ajit.noonia@jaipur.manipal.edu
B.TECH V SEM CSE
ACADEMIC YEAR: 2024-2025
1

2. Divide and
Conquer

3. Divide and
Conquer

4. Recurrence
Relation
A recurrence relation is an equation that represents
a sequence based on some rule. It helps in finding
the subsequent term (next term) dependent upon
the preceding term (previous term). If we know the
previous term in each series, then we can easily
determine the next term.

5. Recurrences
and Running
Time
• An equation that describes a function in terms of its value
on smaller inputs.
T(n) = T(n-1) + n
• Recurrences arise when an algorithm contains recursive
calls to itself
• What is the actual running time of the algorithm?
• Need to solve the recurrence
• Find an explicit formula for the expression
• Bound the recurrence by an expression that involves n

6. Definition
is a recursive function
ofinteger
⚫ A recurrence relation,
T(n), variable n.
⚫ Like all recursive functions, it has both recursive case and
base case.
⚫ Example:
⚫ The portion of the definition that does not contain T is called
the base case of the recurrence relation; the portion that
contains T is called the recurrent or recursive case.
⚫ Recurrence relations are useful for expressing the running
times (i.e., the number of basic operations executed) of
recursive algorithms.
6

7. 7
Methods for Solving Recurrences
• Iteration method
• Substitution method
• Recursion tree method
• Master method

8. Recurrence Relation Example 1
Void Test(int n)
{
if(n>0)
{
print(“%d”, n);
Test(n-1);
}
}

9. Recurrence
Relation Example 1
Solution

10. Recurrence Relation Example 2
Void Test(int n)
{
if(n>0)
{
for(i=0; i<n; i++)
{
print(“%d”, n);
}
Test(n-1);
}
}

11. Recurrence
Relation
Example 2
Solution

12. Recurrence Relation Example 3
Void Test(int n)
{
if(n>0)
{
for(i=0; i<n; i=i*2)
{
print(“%d”, i);
}
Test(n-1);
}
}

13. 13
The Iteration Method
• Convert the recurrence into a summation and try to bind it using a
known series
– Iterate the recurrence until the initial condition is reached.
– Use back-substitution to express the recurrence in terms of n and the
initial (boundary) condition.

14. 14
The recursion-tree method
Convert the recurrence into a tree:
– Each node represents the cost incurred at various
levels of recursion
– Sum up the costs of all levels
Used to “guess” a solution for the recurrence

15. Observation

16. Recurrence Relation Example 4

19. Masters Theorem Decreasing Function

20. Masters Theorem Decreasing Function

21. Recurrence Relation Dividing Function
Example 1
Void Test(int n)
{
if(n>1)
{
print(“%d”, n);
Test(n/2);
}
}

24. Recurrence
Relation Dividing
Function
Example 2
•T(n) = T(n/2) + n for n>1
= 1 for n=1

26. Recurrence Relation Dividing Function
Example 3
Void Test(int n)
{
if(n>1)
{
for(i=0; i<n; i++)
{
statement;
}
Test(n/2);
Test(n/2);
}
}

27. T(n) = 2T(n/2) + n for n>1
= 1 for n=1
T(n) = 2T(n/2) + n ---------Eq-1

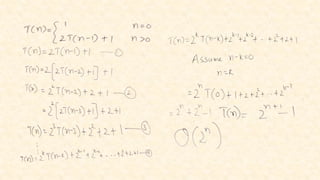
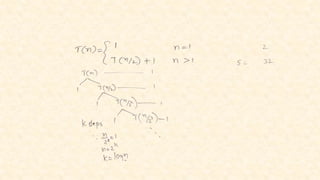
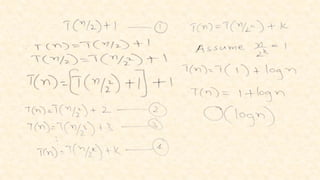
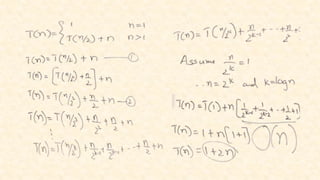
28. 28
Recurrent Algorithms
BINARY-SEARCH
• for an ordered array A, finds if x is in the array A[lo…hi]
Alg.: BINARY-SEARCH (A, lo, hi, x)
if (lo > hi)
return FALSE
mid  (lo+hi)/2
if x = A[mid]
return TRUE
if ( x < A[mid] )
BINARY-SEARCH (A, lo, mid-1, x)
if ( x > A[mid] )
BINARY-SEARCH (A, mid+1, hi, x)
12
11
10
9
7
5
3
2
1 2 3 4 5 6 7 8
mid
lo hi

29. 29
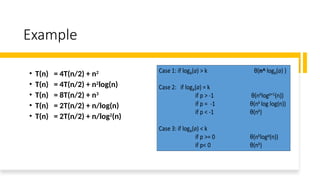
Example
• A[8] = {1, 2, 3, 4, 5, 7, 9, 11}
– lo = 1 hi = 8 x = 7
mid = 4, lo = 5, hi = 8
mid = 6, A[mid] = x
Found!
11
9
7
5
4
3
2
1
11
9
7
5
4
3
2
1
1 2 3 4 5 6 7 8
8
7
6
5

30. 30
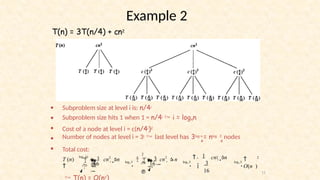
Another Example
• A[8] = {1, 2, 3, 4, 5, 7, 9, 11}
– lo = 1 hi = 8 x = 6
mid = 4, lo = 5, hi = 8
mid = 6, A[6] = 7, lo = 5, hi = 5
11
9
7
5
4
3
2
1
11
9
7
5
4
3
2
1
1 2 3 4 5 6 7 8
11
9
7
5
4
3
2
1 mid = 5, A[5] = 5, lo = 6, hi = 5
NOT FOUND!
11
9
7
5
4
3
2
1
low high
low
low
high
high

31. 31
Analysis of BINARY-SEARCH
Alg.: BINARY-SEARCH (A, lo, hi, x)
if (lo > hi)
return FALSE
mid  (lo+hi)/2
if x = A[mid]
return TRUE
if ( x < A[mid] )
BINARY-SEARCH (A, lo, mid-1, x)
if ( x > A[mid] )
BINARY-SEARCH (A, mid+1, hi, x)
• T(n) = c +
– T(n) – running time for an array of size n
constant time: c2
same problem of size n/2
same problem of size n/2
constant time: c1
constant time: c3
T(n/2)

32. 32
The Iteration Method
T(n) = c + T(n/2)
T(n) = c + T(n/2)
= c + c + T(n/4)
= c + c + c + T(n/8)
Assume n = 2k
T(n) = c + c + … + c + T(1)
= clgn + T(1)
= Θ(lgn)
k times
T(n/2) = c + T(n/4)
T(n/4) = c + T(n/8)

33. Masters Theorem in Algorithms for Dividing Function
T(n) = aT(n/b) +
f(n)
where n = size of the problem
a = number of subproblems in the recursion and a >=
1
n/b = size of each subproblem
b > 1, k >= 0 and p is a real number.
Case 1: if logb(a) > k θ(n^ logb(a) )
Case 2: if logb(a) = k
if p > -1 θ(nk
logp+1
(n))
if p = -1 θ(nk
log log(n))
if p < -1 θ(nk
)
Case 3: if logb(a) < k
if p >= 0 θ(nk
logp
(n))
if p< 0 θ(nk
)

34. T(n) = 2T(n/2) + 1

35. Example
• T(n) = 4T(n/2) + n
• T(n) = 8T(n/2) + n
• T(n) = 9T(n/3) + 1
• T(n) = 8T(n/2) + n.log(n)

36. Example
T(n) = 2T(n/2) + n

37. Example
• T(n) = 4T(n/2) + n2
• T(n) = 4T(n/2) + n2
log(n)
• T(n) = 8T(n/2) + n3
• T(n) = 2T(n/2) + n/log(n)
• T(n) = 2T(n/2) + n/log2
(n)

38. Example
•T(n) = T(n/2) + n2
•T(n) = 2T(n/2) + n2
log2
(n)

39. Recursion-tree method
• A recursion tree models the costs (time) of a recursive
execution of an algorithm.
• The recursion tree method is good for generating guesses
for the substitution method.
• Convert the recurrence into a tree:
• – Each node represents the cost incurred at various levels of recursion
• – Sum up the costs of all levels

40. Solving Recurrences using Recursion Tree Method
• Here while solving recurrences, we divide the problem into subproblems of equal size.
• For e.g., T(n) = a T(n/b) + f(n) where a > 1 ,b > 1 and f(n) is a given function .
F(n) is the cost of splitting or combining the subproblems.
n
T n/b T n/b

41. 10
W(n) = 2W(n/2) + n2
Subproblem size at level i is: n/2i
Subproblem size hits 1 when 1 = n/2i i = lgn
Cost of the problem at level i = (n/2i)2 No. of nodes at level i = 2i
Total cost:
2
1
1 1
 1

i
W (n)    2lg n
W (1)  n2
  n  n2
   O(n) n2
 O(n)  2n2

i 0  2

i 0  2

lg n1
n2 lg n1
 1

i
i 0 2i
 W(n) = O(n2)
Example 1

42. 11
Example 2
T(n) = 3T(n/4) + cn2
•
•
•
•
•
Subproblem size at level i is: n/4i
Subproblem size hits 1 when 1 = n/4i  i = log4n
Cost of a node at level i = c(n/4i)2
Number of nodes at level i = 3i  last level has 3log n = nlog 3 nodes
4 4
Total cost:
2
16
1
16
16
2
2
2
2
log4 3
 log4 3
 log4 3


O(n )
1
  cn  n
3
cn   n



 3

i
cn  n 




T (n)




i0

log4 n1
 3

i
i0

43. Example 3 (simpler proof)
W(n) = W(n/3) + W(2n/3) + n
•
n
The longest path from the root to a leaf is:
 (2/3)n  (2/3)2 n  …  1
• Subproblem size hits 1 when 1
=
(2/3)in  i=log3/2n
Cost of the problem at level i = n
Total cost:
•
•
3/
2
 W(n) = O(nlgn)
lg
3
2
W (n)  n  n  ...  n(log n)  n
lg n
 O(n lg
n)

44. L2.44
Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:

45. L2.45
Example of recursion tree
T(n)
Solve T(n) = T(n/4) + T(n/2) + n2
:

46. L2.46
Example of recursion tree
T(n/4) T(n/2)
n2
Solve T(n) = T(n/4) + T(n/2) + n2
:

47. L2.47
Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
n2
(n/4)2 (n/2)2
T(n/16) T(n/8) T(n/8) T(n/4)

48. L2.48
Example of recursion tree
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2 (n/2)2
Q(1)
…
Solve T(n) = T(n/4) + T(n/2) + n2
:
n2

49. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…

50. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2
2
n
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…

51. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2 2
16
5 n
2
n
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…

52. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2 2
16
5 n
2
n
2
256
25 n
…
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…

53. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2 2
16
5 n
2
n
2
256
25 n
…
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…
)

54. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2 2
16
5 n
2
n
2
256
25 n
…
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…
)

55. Example of recursion tree
Solve T(n) = T(n/4) + T(n/2) + n2
:
(n/16)2
(n/8)2
(n/8)2
(n/4)2
(n/4)2 2
16
5 n
2
n
2
256
25 n
…
n2
(n/2)2
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
…
Q(1)
… Q(1)
… Q(1)
…
Q(1)
…
)
n/2i
= 1 => n = 2i
=> i = log2n

56. Example of recursion tree
+ 2i
*T(1)
)i
+ 2log
2
n
For simplicity assume it as an infinity series
)i
+ nlog
2
2
So T(n) = n2
(1 / (1-5/16)) + n
T(n) = n2
(11/16) + n
So T(n) = Q(n2
)