DivideAndConquer.ppt

1. Divide-and-Conquer 1
© 2004 Goodrich, Tamassia
Divide-and-Conquer
7 2  9 4  2 4 7 9
7  2  2 7 9  4  4 9
7  7 2  2 9  9 4  4

2. Divide-and-Conquer 2
© 2004 Goodrich, Tamassia
Divide-and-Conquer
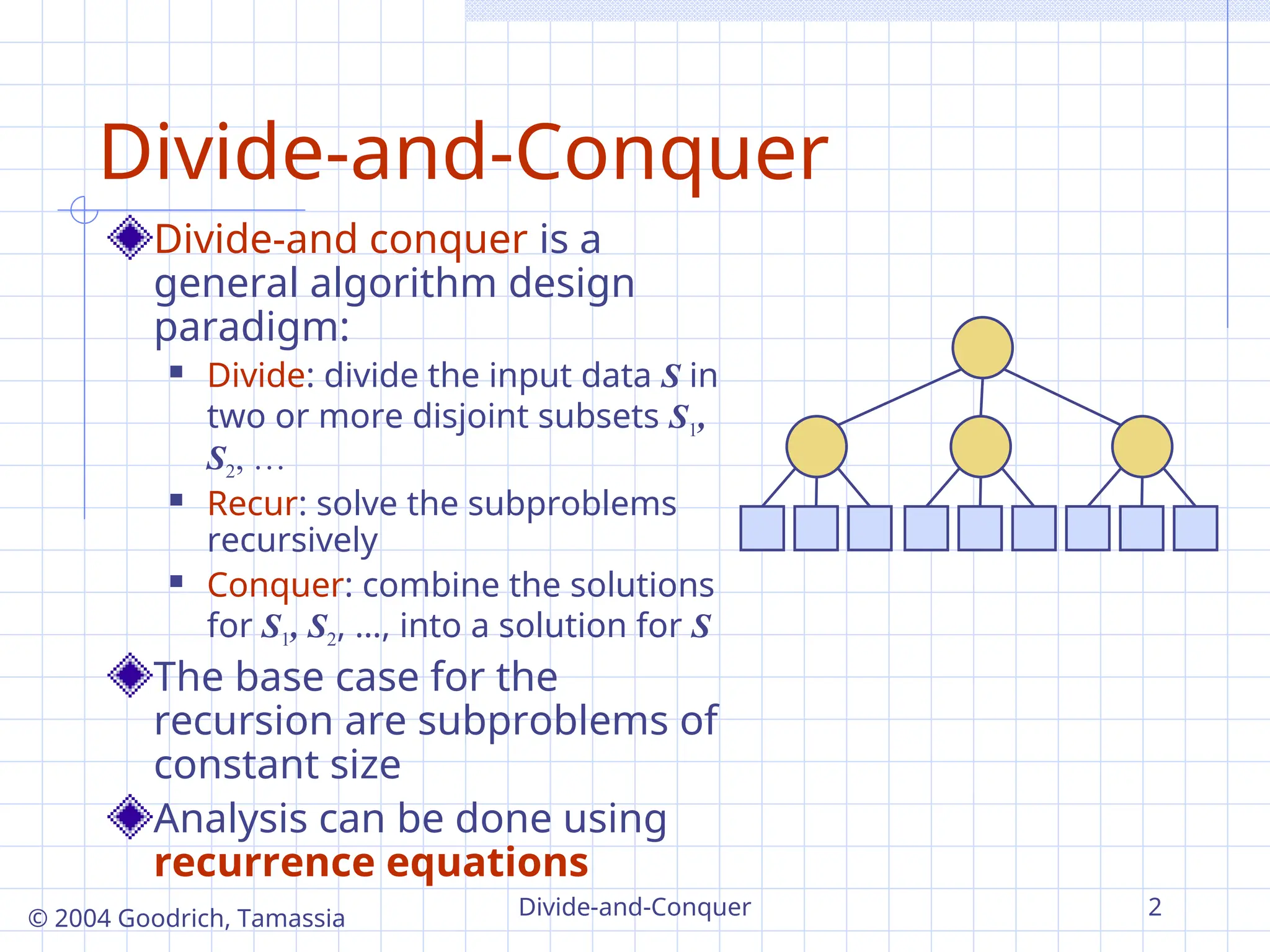
Divide-and conquer is a
general algorithm design
paradigm:
 Divide: divide the input data S in
two or more disjoint subsets S1,
S2, …
 Recur: solve the subproblems
recursively
 Conquer: combine the solutions
for S1, S2, …, into a solution for S
The base case for the
recursion are subproblems of
constant size
Analysis can be done using
recurrence equations

3. Divide-and-Conquer 3
© 2004 Goodrich, Tamassia
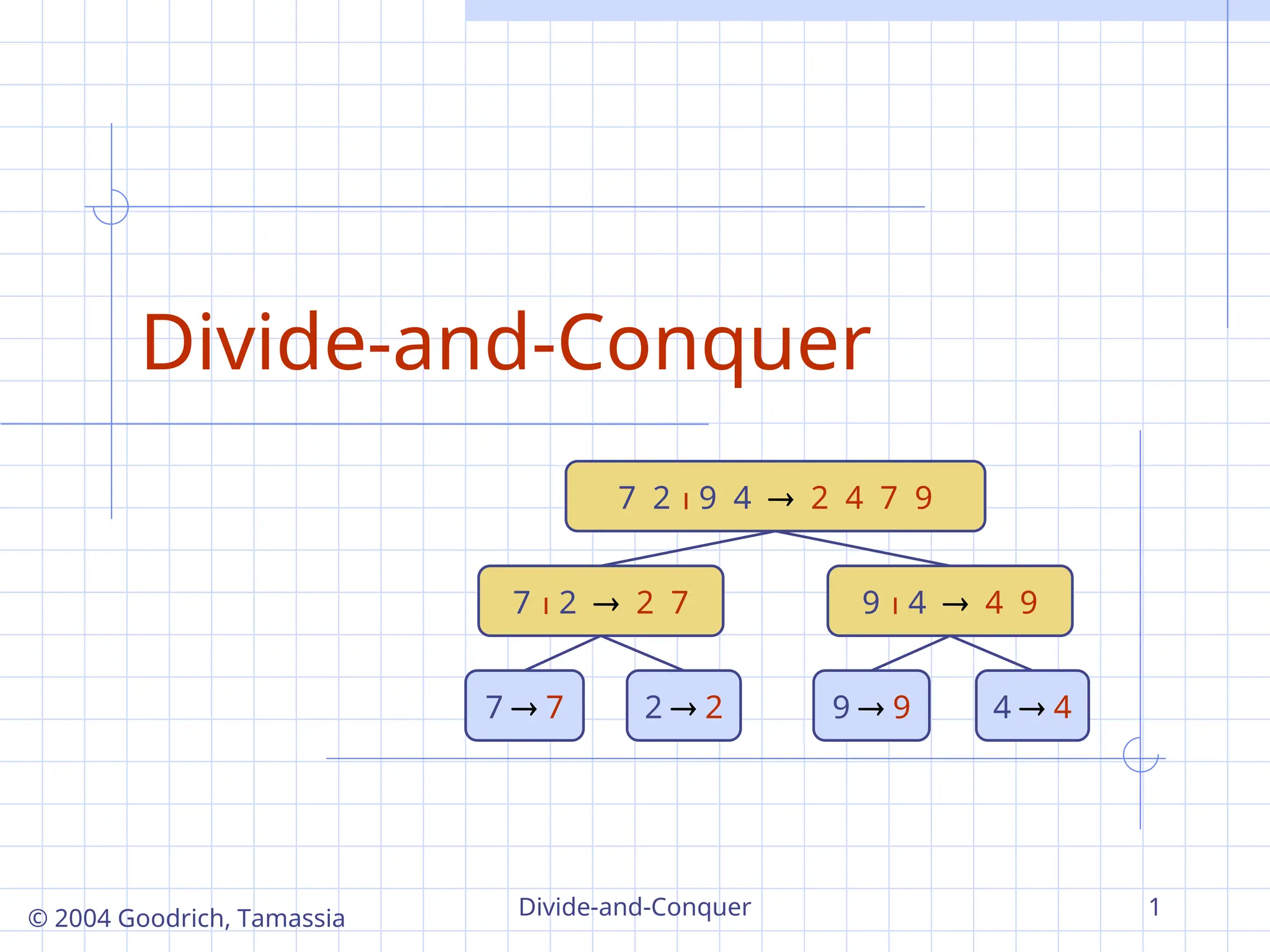
Merge-Sort Review
Merge-sort on an
input sequence S with
n elements consists of
three steps:
 Divide: partition S into
two sequences S1 and S2
of about n2 elements
each
 Recur: recursively sort
S1 and S2
 Conquer: merge S1 and
S2 into a unique sorted
sequence
Algorithm mergeSort(S, C)
Input sequence S with n
elements, comparator C
Output sequence S sorted
according to C
if S.size() > 1
(S1, S2)  partition(S, n/2)
mergeSort(S1, C)
mergeSort(S2, C)
S  merge(S1, S2)

4. Divide-and-Conquer 4
© 2004 Goodrich, Tamassia
Recurrence Equation
Analysis
The conquer step of merge-sort consists of merging two
sorted sequences, each with n2 elements and implemented by
means of a doubly linked list, takes at most bn steps, for some
constant b.
Likewise, the basis case (n < 2) will take at b most steps.
Therefore, if we let T(n) denote the running time of merge-sort:
We can therefore analyze the running time of merge-sort by
finding a closed form solution to the above equation.
 That is, a solution that has T(n) only on the left-hand side.







2
if
)
2
/
(
2
2
if
)
(
n
bn
n
T
n
b
n
T

5. Divide-and-Conquer 5
© 2004 Goodrich, Tamassia
Iterative Substitution
In the iterative substitution, or “plug-and-chug,” technique, we iteratively
apply the recurrence equation to itself and see if we can find a pattern:
Note that base, T(n)=b, case occurs when 2i
=n. That is, i = log n.
So,
Thus, T(n) is O(n log n).
ibn
n
T
bn
n
T
bn
n
T
bn
n
T
bn
n
b
n
T
bn
n
T
n
T
i
i














)
2
/
(
2
...
4
)
2
/
(
2
3
)
2
/
(
2
2
)
2
/
(
2
))
2
/
(
))
2
/
(
2
(
2
)
2
/
(
2
)
(
4
4
3
3
2
2
2
n
bn
bn
n
T log
)
( 


6. Divide-and-Conquer 6
© 2004 Goodrich, Tamassia
The Recursion Tree
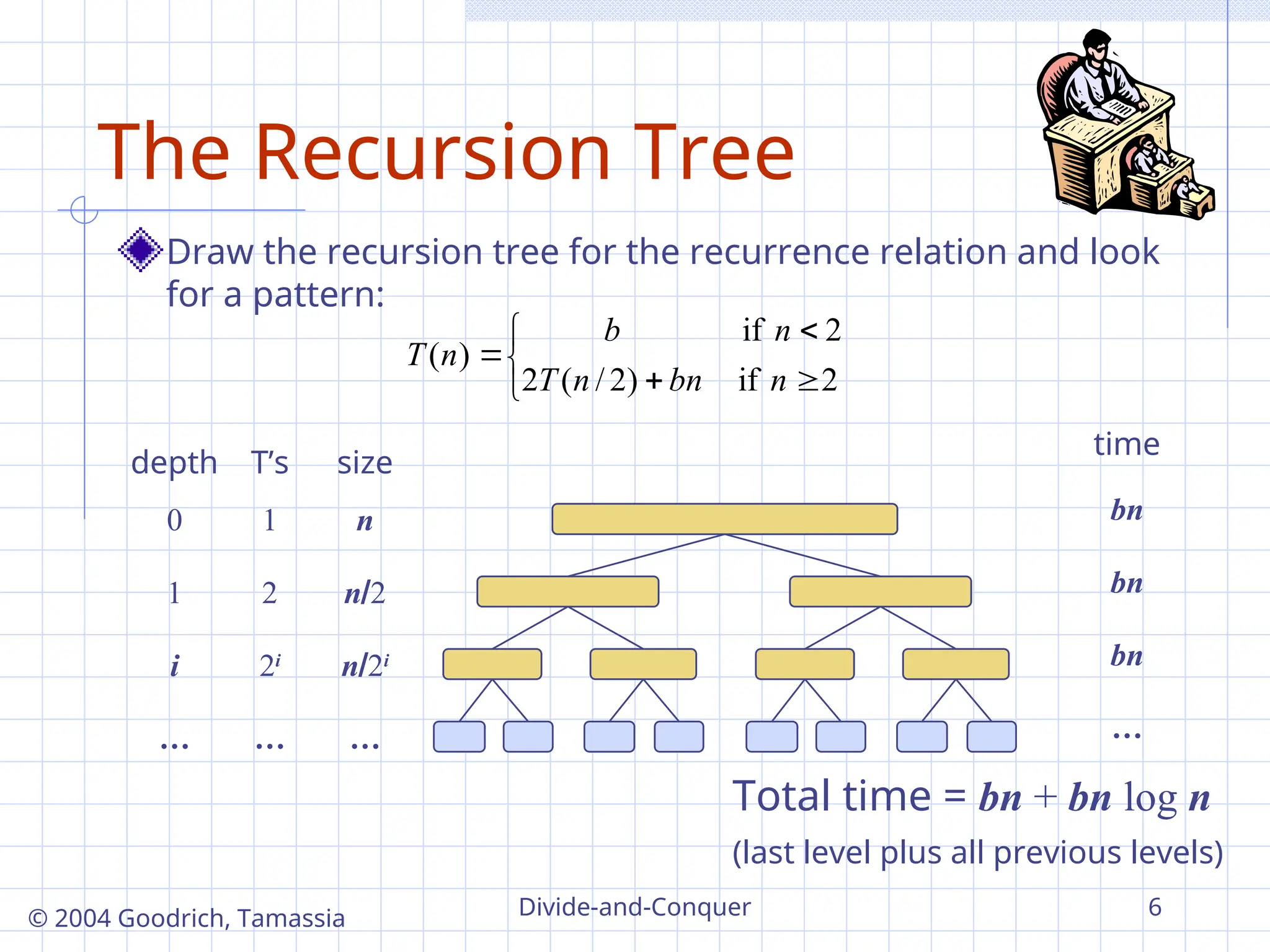
Draw the recursion tree for the recurrence relation and look
for a pattern:
depth T’s size
0 1 n
1 2 n2
i 2i
n2i
… … …







2
if
)
2
/
(
2
2
if
)
(
n
bn
n
T
n
b
n
T
time
bn
bn
bn
…
Total time = bn + bn log n
(last level plus all previous levels)

7. Divide-and-Conquer 7
© 2004 Goodrich, Tamassia
Guess-and-Test Method
In the guess-and-test method, we guess a closed form solution
and then try to prove it is true by induction:
Guess: T(n) < cn log n.
Wrong: we cannot make this last line be less than cn log n
n
bn
cn
n
cn
n
bn
n
cn
n
bn
n
n
c
n
bn
n
T
n
T
log
log
log
)
2
log
(log
log
))
2
/
log(
)
2
/
(
(
2
log
)
2
/
(
2
)
(

















2
if
log
)
2
/
(
2
2
if
)
(
n
n
bn
n
T
n
b
n
T

8. Divide-and-Conquer 8
© 2004 Goodrich, Tamassia
Guess-and-Test Method,
Part 2
Recall the recurrence equation:
Guess #2: T(n) < cn log2
n.
 if c > b.
So, T(n) is O(n log2
n).
In general, to use this method, you need to have a good guess
and you need to be good at induction proofs.
n
cn
n
bn
cn
n
cn
n
cn
n
bn
n
cn
n
bn
n
n
c
n
bn
n
T
n
T
2
2
2
2
log
log
log
2
log
log
)
2
log
(log
log
))
2
/
(
log
)
2
/
(
(
2
log
)
2
/
(
2
)
(



















2
if
log
)
2
/
(
2
2
if
)
(
n
n
bn
n
T
n
b
n
T

9. Divide-and-Conquer 9
© 2004 Goodrich, Tamassia
Master Method
(Appendix)
Many divide-and-conquer recurrence equations
have the form:
The Master Theorem:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b

10. Divide-and-Conquer 10
© 2004 Goodrich, Tamassia
Master Method, Example
1
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
n
n
T
n
T 
 )
2
/
(
4
)
(
Solution: logba=2, so case 1 says T(n) is O(n2
).

11. Divide-and-Conquer 11
© 2004 Goodrich, Tamassia
Master Method, Example
2
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
n
n
n
T
n
T log
)
2
/
(
2
)
( 

Solution: logba=1, so case 2 says T(n) is O(n log2
n).

12. Divide-and-Conquer 12
© 2004 Goodrich, Tamassia
Master Method, Example
3
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
n
n
n
T
n
T log
)
3
/
(
)
( 

Solution: logba=0, so case 3 says T(n) is O(n log n).

13. Divide-and-Conquer 13
© 2004 Goodrich, Tamassia
Master Method, Example
4
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
2
)
2
/
(
8
)
( n
n
T
n
T 

Solution: logba=3, so case 1 says T(n) is O(n3
).

14. Divide-and-Conquer 14
© 2004 Goodrich, Tamassia
Master Method, Example
5
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
3
)
3
/
(
9
)
( n
n
T
n
T 

Solution: logba=2, so case 3 says T(n) is O(n3
).

15. Divide-and-Conquer 15
© 2004 Goodrich, Tamassia
Master Method, Example
6
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
1
)
2
/
(
)
( 
 n
T
n
T
Solution: logba=0, so case 2 says T(n) is O(log n).
(binary search)

16. Divide-and-Conquer 16
© 2004 Goodrich, Tamassia
Master Method, Example
7
The form:
The Master Theorem:
Example:







d
n
n
f
b
n
aT
d
n
c
n
T
if
)
(
)
/
(
if
)
(
.
1
some
for
)
(
)
/
(
provided
)),
(
(
is
)
(
then
),
(
is
)
(
if
3.
)
log
(
is
)
(
then
),
log
(
is
)
(
if
2.
)
(
is
)
(
then
),
(
is
)
(
if
1.
log
1
log
log
log
log














n
f
b
n
af
n
f
n
T
n
n
f
n
n
n
T
n
n
n
f
n
n
T
n
O
n
f
a
k
a
k
a
a
a
b
b
b
b
b
n
n
T
n
T log
)
2
/
(
2
)
( 

Solution: logba=1, so case 1 says T(n) is O(n).
(heap construction)

17. Divide-and-Conquer 17
© 2004 Goodrich, Tamassia
Iterative “Proof” of the
Master Theorem























1
)
(log
0
log
1
)
(log
0
log
2
2
3
3
2
2
2
)
/
(
)
1
(
)
/
(
)
1
(
.
.
.
)
(
)
/
(
)
/
(
)
/
(
)
(
)
/
(
)
/
(
))
/
(
))
/
(
(
)
(
)
/
(
)
(
n
i
i
i
a
n
i
i
i
n
b
b
b
b
b
n
f
a
T
n
b
n
f
a
T
a
n
f
b
n
af
b
n
f
a
b
n
T
a
n
f
b
n
af
b
n
T
a
bn
b
n
f
b
n
aT
a
n
f
b
n
aT
n
T

18. Divide-and-Conquer 18
© 2004 Goodrich, Tamassia
Integer Multiplication
Algorithm: Multiply two n-bit integers I and J.
 Divide step: Split I and J into high-order and low-order bits
 We can then define I*J by multiplying the parts and adding:
 So, T(n) = 4T(n/2) + n, which implies T(n) is O(n2
).
 But that is no better than the algorithm we learned in
grade school.
l
n
h
l
n
h
J
J
J
I
I
I




2
/
2
/
2
2
l
l
n
h
l
n
l
h
n
h
h
l
n
h
l
n
h
J
I
J
I
J
I
J
I
J
J
I
I
J
I







2
/
2
/
2
/
2
/
2
2
2
)
2
(
*
)
2
(
*

19. Divide-and-Conquer 19
© 2004 Goodrich, Tamassia
An Improved Integer
Multiplication Algorithm
Algorithm: Multiply two n-bit integers I and J.
 Divide step: Split I and J into high-order and low-order bits
 Observe that there is a different way to multiply parts:
 So, T(n) = 3T(n/2) + n, which implies T(n) is O(nlog
2
3
), by the
Master Theorem.
 Thus, T(n) is O(n1.585
).
l
n
h
l
n
h
J
J
J
I
I
I




2
/
2
/
2
2
l
l
n
h
l
l
h
n
h
h
l
l
n
l
l
h
h
h
l
h
h
l
l
l
h
n
h
h
l
l
n
l
l
h
h
h
l
l
h
n
h
h
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
I
J
J
I
I
J
I
J
I



















2
/
2
/
2
/
2
)
(
2
2
]
)
[(
2
2
]
)
)(
[(
2
*