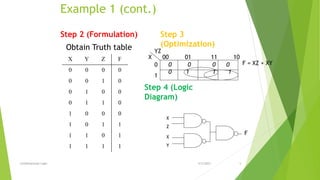
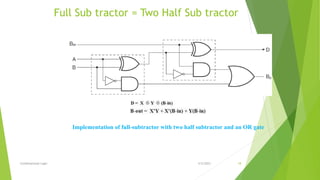
The document discusses combinational logic circuits including adders, subtractors, and their design process. It begins with an overview of combinational vs sequential circuits. The design procedure is then outlined as starting with a specification, formulating a truth table, optimizing with K-maps or algebra, and developing the logic diagram. Examples are provided to design a 3-input/1-output circuit, BCD to excess-3 converter, half and full adders/subtractors. Exercise problems are also listed at the end involving designing incrementers, decrementers, and equality comparators.

1. Lecture 8 Agenda:
 Combinational Circuits
 Design Procedure
 Half, Full and Parallel Adder
 Half and Full Subtractor

2. Combinational circuits
 Consists of logic gates whose
output depends on only the
present input.
 Example: Adder
1
0
+________
1
Sequential circuits
 Consists of logic gates + storage
elements. Output depends on inputs
and the state of the storage elements
or previous outputs.
 Example: Counter
 4+1 5
 3+14
5/2/2023
Combinational Logic 2
• Logic circuits for digital systems may be….
Introduction
Sequential circuits are the building blocks of digital systems
and will be discussed in next chapter.

3. Design Procedure
 Starts from the specification of the problem, which leads
to the truth table. Using the output values of truth table,
the logic equation and simplified using K maps, or
Algebraic manipulation. The equation of the output
functions, the corresponding circuit is found. The process
is shown in Figure:
5/2/2023
Logic Diagram
Verification Specification
Optimization
K-Map Boolean Algebra
Formulation
Truth Table Boolean Equation
Specification
Goal Functionality
Combinational Logic 3

4. Example 1
 Design a circuit that has a 3-bit input and a single
output (F) specified as follows:
• F = 0, when the input is less than (5)
• F = 1, otherwise
Solution:
 Step 1 (Specification):
• Label the inputs (3 bits) as X, Y, Z
• X is the most significant bit, Z is the least significant bit
• The output (1 bit) is F:
• F = 1  (101)2, (110)2, (111)2
• F = 0  other inputs
5/2/2023
Combinational Logic 4

5. Step 2 (Formulation)
Obtain Truth table
X Y Z F
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
X
YZ
0
1
00 01 11 10
0 0 0 0
0 1 1 1
Step 3
(Optimization)
F = XZ + XY
X
Z
X
Y
F
Example 1 (cont.)
Step 4 (Logic
Diagram)
5/2/2023
Combinational Logic 5

6. BCD Input Excess 3 Output
Decimal A B C D W X Y Z
0 0 0 0 0 0 0 1 1
1 0 0 0 1 0 1 0 0
2 0 0 1 0 0 1 0 1
3 0 0 1 1 0 1 1 0
4 0 1 0 0 0 1 1 1
5 0 1 0 1 1 0 0 0
6 0 1 1 0 1 0 0 1
7 0 1 1 1 1 0 1 0
8 1 0 0 0 1 0 1 1
9 1 0 0 1 1 1 0 0
10-15 All other inputs X X X X
Step 1 (Specification)
 4-bit BCD input (A,B,C,D)
 4-bit E-3 output (W,X,Y,Z)
Design Example 2:
BCD to Excess-3 Converter
Step 2 (Formulation)
Obtain Truth table
5/2/2023
Combinational Logic 6

7. Example 2 (cont.)
Step 3
(Optimization)
Step 4 (Logic
Diagram)
5/2/2023
Combinational Logic 7

8. Exercise Problems
Problem 4.4
Design a combinational circuit with three inputs and one output.
(a) The output is 1 when the binary value of the inputs is less than 3. The output is 0 otherwise.
(b) The output is 1 when the binary value of the inputs is an even number.
Problem 4.5
Design a combinational circuit with three inputs, x , y , and z , and three outputs, A, B , and C.
When the binary input is 0, 1, 2, or 3, the binary output is one greater than the input. When the
binary input is 4, 5, 6, or 7, the binary output is two less than the input.
Problem 4.6
A majority circuit is a combinational circuit whose output is equal to 1 if the input variables
have more 1’s than 0’s. The output is 0 otherwise. Design a 3-input majority circuit by finding the
circuit’s truth table, Boolean equation, and a logic diagram.

9. Exercise Problems
Problem 4.7
Design a combinational circuit that converts a four-bit Gray code to a four bit binary
number. Implement the circuit with exclusive-OR gates.

10. BINARY ADDER–SUBTRACTOR
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
 A combinational circuit that performs the addition of two bits is called a half
adder .
 One that performs the addition of three bits is a full adder .
 half adders + half adders = full adder.
5/2/2023
Combinational Logic 10

11. Half Adder
5/2/2023
Step 3
(Optimization)
Step 4 (Logic
Diagram)
Step 1
(Specification)
Step 2 (Formulation)
Combinational Logic 11

12. Full Adder
5/2/2023
Step 1
(Specification)
Step 2 (Formulation)
Combinational Logic 12

13. 5/2/2023
Full Adder
Step 3
(Optimization)
Step 4 (Logic
Diagram)
Combinational Logic 13

14. 5/2/2023
Full Adder = Two Half Adder
Combinational Logic 14

15. Half Sub tractor
5/2/2023
Step 3
(Optimization) Step 4 (Logic
Diagram)
Step 1
(Specification)
Step 2 (Formulation)
Combinational Logic 15

16. Full Sub tractor
5/2/2023
Step 1
(Specification)
Step 2 (Formulation)
X-Y-Z
Combinational Logic 16

17. 5/2/2023
Full Sub tractor
Step 3
(Optimization) Step 4 (Logic
Diagram)
Combinational Logic 17

18. 5/2/2023
Full Sub tractor = Two Half Sub tractor
Implementation of full-subtractor with two half subtractor and an OR gate
Combinational Logic 18

19. Exercise Problems
Problem 4.11
Using four half-adders,
(a) Design a full adder circuit incrementer. (A circuit that adds one to a four bit
binary number.)
(b) Design a four-bit combinational decrementer (a circuit that subtracts 1 from a four bit
binary number).
Problem 4.21
Design a combinational circuit that compares two 4-bit numbers to check if they are equal. The
circuit output is equal to 1 if the two numbers are equal and 0 otherwise.