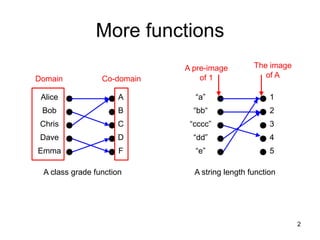
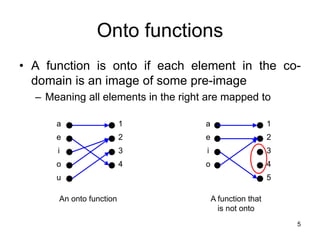
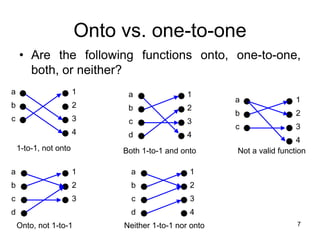
1. A function maps each element from a set (domain) to a unique element in another set (co-domain). 2. A one-to-one (injective) function maps each domain element to a unique co-domain element, while an onto (surjective) function maps all co-domain elements to domain elements. 3. A bijection is a function that is both one-to-one and onto, providing a perfect pairing between each domain and co-domain element.

1. 1
Definition of a function
• A function takes an element from a set and
maps it to a UNIQUE element in another set

2. 2
More functions
1
2
3
4
5
“a”
“bb“
“cccc”
“dd”
“e”
A string length function
A
B
C
D
F
Alice
Bob
Chris
Dave
Emma
A class grade function
Domain Co-domain
A pre-image
of 1
The image
of A

3. 3
One-to-one functions
1
2
3
4
5
a
e
i
o
A one-to-one function
1
2
3
4
5
a
e
i
o
A function that is
not one-to-one
• A function is one-to-one if each element in the
co-domain has a unique pre-image
– Meaning no 2 values map to the same result

4. 4
More on one-to-one
• Injective is synonymous with one-to-one
– “A function is injective”
• A function is an injection if it is one-to-one
• Note that there can
be un-used elements
in the co-domain
1
2
3
4
5
a
e
i
o
A one-to-one function

5. 5
Onto functions
1
2
3
4
5
a
e
i
o
A function that
is not onto
• A function is onto if each element in the co-
domain is an image of some pre-image
– Meaning all elements in the right are mapped to
1
2
3
4
a
e
i
o
u
An onto function

6. 6
1
2
3
4
a
e
i
o
u
An onto function
More on onto
• Surjective is synonymous with onto
– “A function is surjective”
• A function is an surjection if it is onto
• Note that there can
be multiply used
elements in the
co-domain

7. 7
Onto vs. one-to-one
• Are the following functions onto, one-to-one,
both, or neither?
1
2
3
4
a
b
c
1
2
3
a
b
c
d
1
2
3
4
a
b
c
d
1
2
3
4
a
b
c
d
1
2
3
4
a
b
c
1-to-1, not onto
Onto, not 1-to-1
Both 1-to-1 and onto Not a valid function
Neither 1-to-1 nor onto

8. 8
Bijections
• Consider a function that is
both one-to-one and onto:
• Such a function is a one-to-one correspondence,
or a bijection
1
2
3
4
a
b
c
d