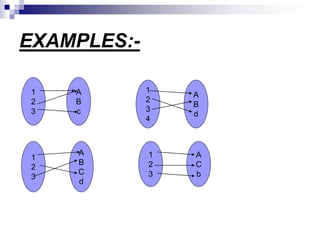
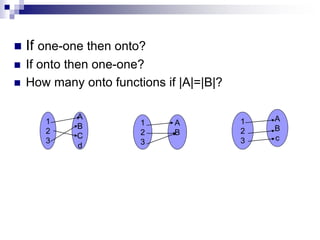
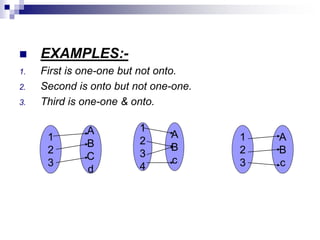
The document summarizes different types of functions: one-to-one functions, onto functions, and bijective functions. It provides definitions and examples of each. For one-to-one functions, it explains that each element in the domain maps to a unique element in the codomain. For onto functions, it explains that each element in the codomain is mapped to by at least one element in the domain. A bijective function is both one-to-one and onto, so it establishes a perfect pairing between the elements of the domain and codomain. The document also discusses relationships between these types of functions and how to determine the number of possible functions between sets of different sizes.

1. BS SE(1B)EVENING
COURSE:DISCRETE STRUCTURE
UIIT
GROUP NO:8
GROUP MEMBERS:
1.SAJAL ASGHAR
2.M.MUAWWAZ USMAN
3.M.SAAD MALIK
UIIT(UNIVERSITY INSTITUTE OF INFORMATION TECHNOLOGY)

2. OUTLINE OF TODAY’S
PRESENTTATION:
 ONE-ONE FUNCTION.
 ONTO FUNCTION
 BIJECTIVE FUNCTION.

3. ONE-ONE
FUNCTION(INJECTIVE)
DEFINATION:-
“A function of from set ‘A’ to set ‘B’ is one-one
Function if no two elements in ‘A’ are mapped
To same element in ‘B’ ”
 Distinct elements form distinct images.
 We cannot mapped with same elements.
 Value of ‘x’ elements must be equal to ’y’.
 Value of ‘y’ must be greater than ‘x’.

4. EXAMPLES:-
1
2
3
A
B
c
1
2
3
4
A
B
d
1
2
3
A
B
C
d
1
2
3
A
C
b

5.  |A|<|B|
 How many one to one functions are possible?
 Total number of element in set ‘A’ is |x|.
 Total number of elements in set ‘B’ is |Y|.
 I have ‘y’ number of choices for first element of set ‘A’.
 {y(y-1) (y-2) (y-3)…….y-(x-1)}
So we can derive formula from this series.
 yPx =4P3 this is how to write formula
1
2
3
A
C
B
k

6. ONTO FUNCTION (surjection)
DEFINATION:-
‘A function ‘f’ from set ‘A’ to set ‘B’ is onto if each element of
’B’ is mapped to at least one element of ‘A’.
 Range of f=B.
 In onto function range equals to the elements of set B.
 If both range and co-domains are equal so it is onto
function.
 |A|>|B|
A
B
C
1
2
3
1
2
3
A
B

7.  If one-one then onto?
 If onto then one-one?
 How many onto functions if |A|=|B|?
1
2
3
A
B
1
2
3
A
B
C
d
1
2
3
A
B
c

8. BIJECTIVE FUNCTION:
DEFINATION:-
“A Function f : A&B bijection if ‘f’ is both one-one & onto.”
 One-one function:- ( |A| < |B| )
 Onto function:- ( |A| > |B| )
 If you want to make bijective function then number of
element of set ‘A’ must be equal to the elements of set of
set ‘B’. |A|=|B|

9.  EXAMPLES:-
1. First is one-one but not onto.
2. Second is onto but not one-one.
3. Third is one-one & onto.
1
2
3
4
A
B
c
1
2
3
A
B
C
d
1
2
3
A
B
c