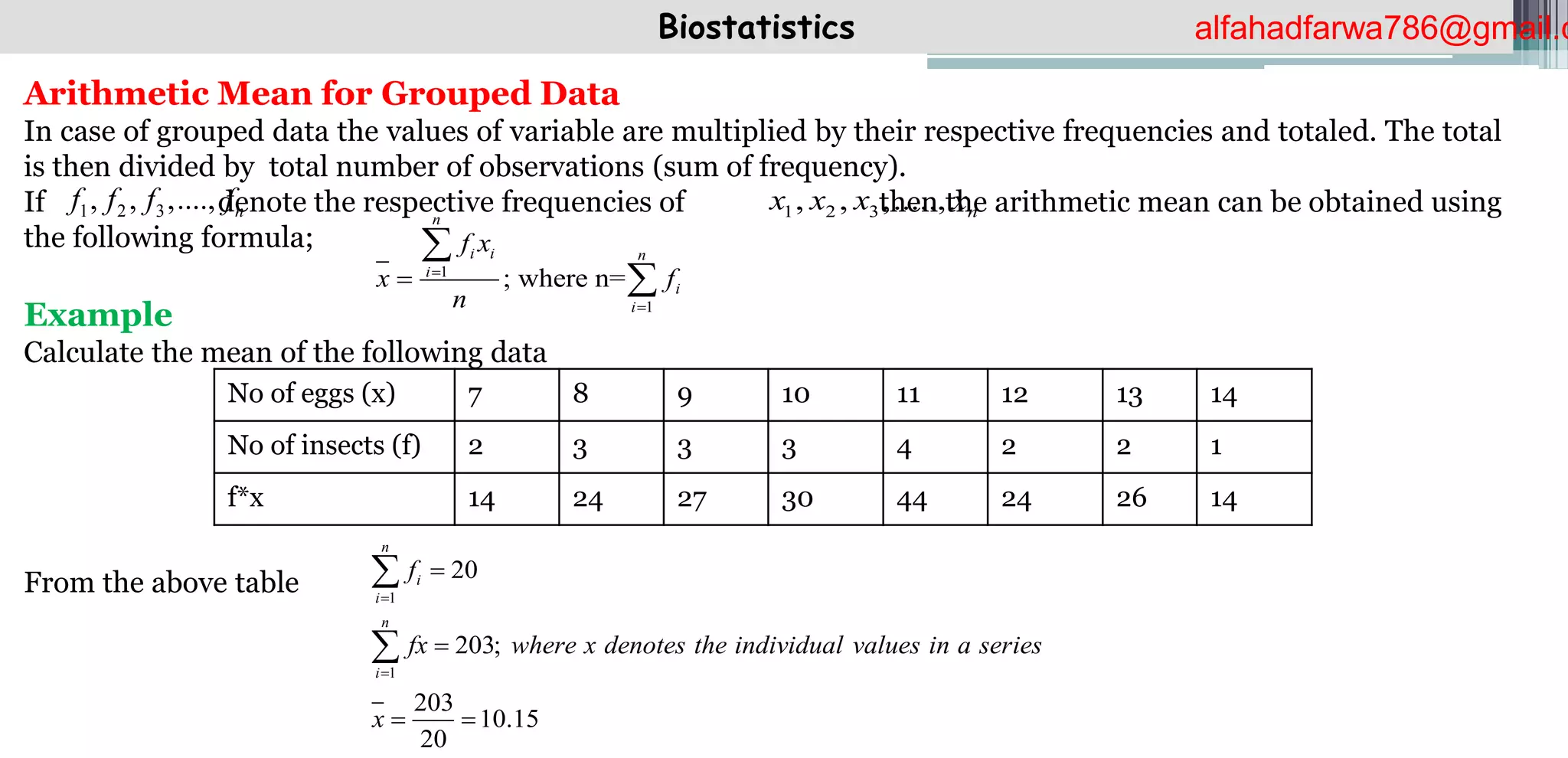
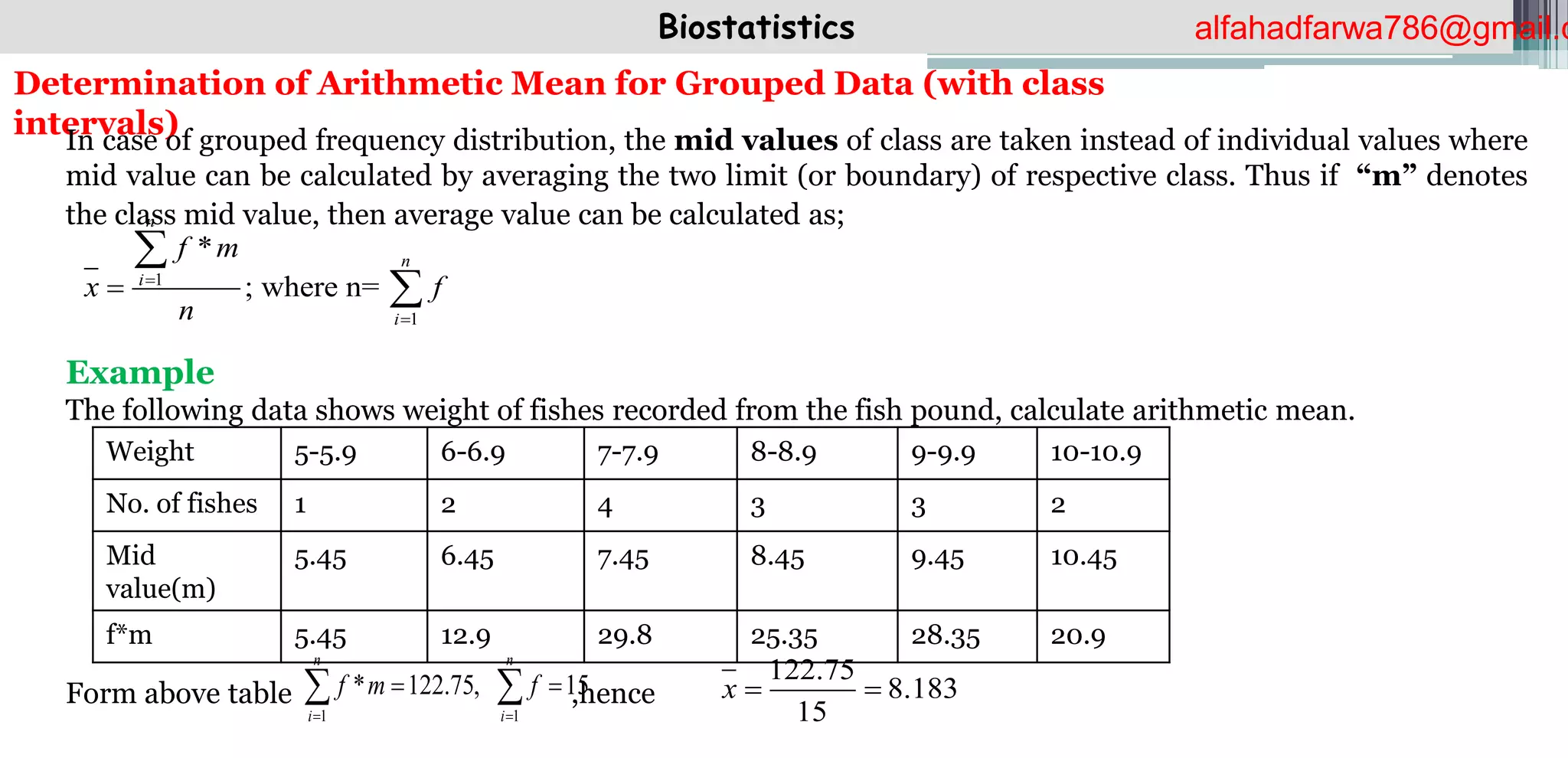
The document discusses the concept of arithmetic mean in biostatistics, detailing methods for calculating it for both ungrouped and grouped data. It includes formulas, examples with plasma potassium values and plant heights, and outlines important properties of the arithmetic mean. The document serves as an educational resource for understanding statistical analysis in biological research.

1. Biostatistics
Lecture N0 07
alfahadfarwa786@gmail.c
Muhammad Alfahad
Farfwa Butt

2. Biostatistics
Arithmetic Mean (AM)
Arithmetic mean of a series is obtained by dividing total of values in series by the number of items i.e.
Arithmetic mean is denoted by .
Determination of Arithmetic Mean for Ungrouped Data
Let be the “n” values of variable , then the arithmetic mean can be obtained by using the
following formula:
1 2 3
, , ,......., n
x x x x X
1 2 3
1
1
[ ..... ]
1
, where is arithmetic mean, = summation symbol
n
n
i
i
x x x x x
n
x x
n 
    
  

sum of all values
Mean=
total number of values
x
alfahadfarwa786@gmail.c

3. Biostatistics
Example:
The following are plasma potassium values (mmol/l) of 14 dogs:
4.37, 4.87, 4.35, 3.92, 4.68, 4.54, 5.24, 4.57, 4.59, 4.66, 4.40, 4.73, 4.83, 4.21.
Solution:
Example
The following data is the final plant height (cm) of thirty plants of wheat. Calculate
Arithmetic mean.
87, 91, 89, 88, 89, 91, 87, 92, 90, 98, 95, 97, 96, 100, 101, 96, 98, 99, 98, 100, 102, 99, 101, 105, 103, 107, 105,
106, 107, 112.
Mean
14
Mean 4.57mmol/l
4.37 4.87 4.35 3.92 4.68 4.54 5.24 4.57 4.59 4.66 4.40 4.73 4.83 4.21
           



1 2 .... 2929
97.63
30
n
x x x
x =
n
  
 
alfahadfarwa786@gmail.c

4. Biostatistics
Arithmetic Mean for Grouped Data
In case of grouped data the values of variable are multiplied by their respective frequencies and totaled. The total
is then divided by total number of observations (sum of frequency).
If denote the respective frequencies of then the arithmetic mean can be obtained using
the following formula;
Example
Calculate the mean of the following data
From the above table
1 2 3
, , ,...., n
f f f f 1 2 3
, , ,....., n
x x x x
1
1
; where n=
n
i i n
i
i
i
f x
x f
n





No of eggs (x) 7 8 9 10 11 12 13 14
No of insects (f) 2 3 3 3 4 2 2 1
f*x 14 24 27 30 44 24 26 14
1
1
20
203;
203
10.15
20
n
i
i
n
i
f
fx where x denotes the individual values in a series
x




 


alfahadfarwa786@gmail.c

5. Biostatistics
Determination of Arithmetic Mean for Grouped Data (with class
intervals)
In case of grouped frequency distribution, the mid values of class are taken instead of individual values where
mid value can be calculated by averaging the two limit (or boundary) of respective class. Thus if “m” denotes
the class mid value, then average value can be calculated as;
Example
The following data shows weight of fishes recorded from the fish pound, calculate arithmetic mean.
Form above table ,hence
1
1
*
; where n=
n
n
i
i
f m
x f
n





Weight 5-5.9 6-6.9 7-7.9 8-8.9 9-9.9 10-10.9
No. of fishes 1 2 4 3 3 2
Mid
value(m)
5.45 6.45 7.45 8.45 9.45 10.45
f*m 5.45 12.9 29.8 25.35 28.35 20.9
122.75
8.183
15
x  
1 1
* 122.75, 15
n n
i i
f m f
 
 
 
alfahadfarwa786@gmail.c

6. Biostatistics
Example: Calculate arithmetic mean for the following groped data.
Class
Limits
Class
Boundaries
Mid Points
X
C.F Frequency
(f)
fx
86---90
91---95
96---100
101---105
106---110
111---115
85.5---90.5
90.5---95.5
95.5---100.5
100.5--105.5
105.5– 10.5
110.5--115.5
88
93
98
103
108
113
6
10
20
26
29
30
6
4
10
6
3
1
528
372
980
618
324
113
Solution:
1 2 3 k
1 2 3 k
1 2 3 k
+ + ... x
f f f f fx
x x x
X = =
+ + ... f
f f f f


For grouped data
83
.
97
30
2935




f
fx
=
X
alfahadfarwa786@gmail.c

7. Biostatistics
Important Properties of the Arithmetic Mean
1.
The sum of deviation from the arithmetic mean is equal to zero.
2.
The sum of squared deviations from the arithmetic mean is smaller than the sum of squared deviations from
any other value.
3. If
( ) 0
i
y y
 

2
( ) minimum
i
y y
 

, where "a" and "b"are any two numbers and a 0, then y = ax + b
i i
y ax b
  
alfahadfarwa786@gmail.c