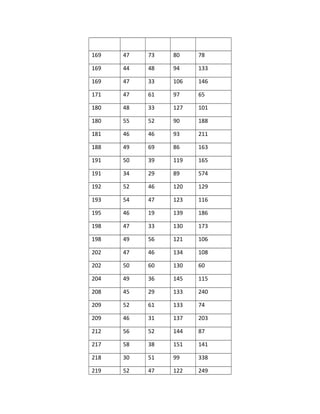
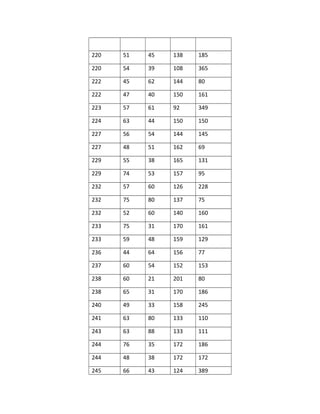
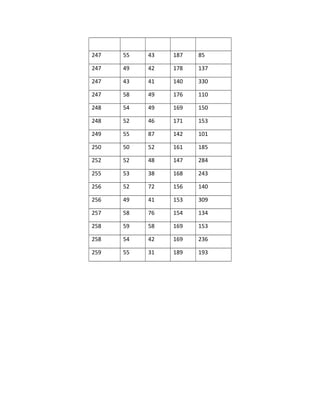
Laporan praktikum metode statistika II membahas tiga permasalahan yaitu pengaruh suhu dan jenis bahan terhadap produktivitas batere, pengaruh generasi dosen pengajar terhadap standar penilaian, dan pengaruh faktor-faktor terhadap kadar kolesterol. Laporan ini meliputi uji asumsi, uji hipotesis, dan analisis regresi untuk menjawab permasalahan-permasalahan tersebut.

1. LAPORAN
PRAKTIKUM METODE STATISTIKA II
Dosen Pengampu :
Drs.Zulaela,Dipl. Med. Stats., M.Si.
Assisten Praktikum :
Ambar Kusumawati ( 12694 )
Isfatun Chasanah ( 12041 )
Disusun oleh :
ADHITYA AKBAR
10/297716/PA/13065
LABORATORIUM KOMPUTASI
MATEMATIKA DAN STATISTIKA
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS GADJAH MADA
YOGYAKARTA
2011

2. BAB I
PERMASALAHAN
1. Sebuah perusahaan batere ingin memproduksi batere yang dapat digunakan pada suhu
ekstrim (rendah atau tinggi). Dipilih 4 jenis bahan batere yang akan dicobakan pada
suhu 15 C, 30 C, dan 45 C
15 30 45
bahan 1
130
155
74
180
34
40
80
75
20
70
82
58
bahan 2
150
188
159
126
136
122
106
115
25
70
58
45
bahan 3
138
110
168
160
174
120
150
139
96
104
82
60
a. Lakukan uji asumsi lengkap!
b. Apakah ada interaksi antara jenis bahan dan suhu?
c. Bahan mana yang memberikan produktifitas batere paling tinggi? Suhu berapa kah yang
memberikan produktifitas batere paling rendah?

3. 2. Suatu penelitian dilakukan untuk mengetahui pengaruh perbedaan generasi dosen
pengajar dengan standar penilaian mata kuliah yang diajarkan. Generasi dosen
dikategorikan sebagai dosen muda dan dosen tua, sedangkan untuk keperluan tersebut
diambil sampel secara acak 160 mahasiswa. Diperoleh hasil bahwa terdapat 80
mahasiswa menjawab dosen tua dan mahasiswa yang menyatakan memberi nilai buruk
sebanyak 31 mahasiswa dan sisanya menyatakan memberi nilai baik. Sedangkan 80
mahasiswa lainnya menjawab dosen muda dan yang menyatakan memberikan nilai
buruk sebanyak 18 mahasiswa dan sisanya menyatakan memberi nilai baik.
a. Uji apakah yang digunakan dalam penelitian tersebut? Sebut dan jelaskan alasannya!
b. Lakukan uji tersebut secara lengkap dan berilah kesimpulan!
c. Berdasarkan analisis tersebut, apakah perlu menggunakan OR? Jelaskan jawaban Anda!
3. Seorang ahli kesehatan ingin melihat pengaruh umur, tingkat HDL, tingkat LDL, dan
tingkat triglyceride terhadap tingkat kolesterol seseorang. Lakukan analisis regresi
secara lengkap hingga didapat model yang baik!! Beri interpretasi!!!
Kolesterol Umur HDL LDL Trygliceride
104 35 31 54 95
105 36 39 39 135
138 39 56 78 133
140 44 53 65 111
140 32 38 82 102
141 44 51 68 106
146 48 41 63 208
151 45 25 86 202
156 44 58 71 133
164 43 50 103 55
165 48 58 81 130
166 68 38 104 116
168 49 38 98 158
169 46 51 101 84

4. 169 47 73 80 78
169 44 48 94 133
169 47 33 106 146
171 47 61 97 65
180 48 33 127 101
180 55 52 90 188
181 46 46 93 211
188 49 69 86 163
191 50 39 119 165
191 34 29 89 574
192 52 46 120 129
193 54 47 123 116
195 46 19 139 186
198 47 33 130 173
198 49 56 121 106
202 47 46 134 108
202 50 60 130 60
204 49 36 145 115
208 45 29 133 240
209 52 61 133 74
209 46 31 137 203
212 56 52 144 87
217 58 38 151 141
218 30 51 99 338
219 52 47 122 249

5. 220 51 45 138 185
220 54 39 108 365
222 45 62 144 80
222 47 40 150 161
223 57 61 92 349
224 63 44 150 150
227 56 54 144 145
227 48 51 162 69
229 55 38 165 131
229 74 53 157 95
232 57 60 126 228
232 75 80 137 75
232 52 60 140 160
233 75 31 170 161
233 59 48 159 129
236 44 64 156 77
237 60 54 152 153
238 60 21 201 80
238 65 31 170 186
240 49 33 158 245
241 63 80 133 110
243 63 88 133 111
244 76 35 172 186
244 48 38 172 172
245 66 43 124 389

6. 247 55 43 187 85
247 49 42 178 137
247 43 41 140 330
247 58 49 176 110
248 54 49 169 150
248 52 46 171 153
249 55 87 142 101
250 50 52 161 185
252 52 48 147 284
255 53 38 168 243
256 52 72 156 140
256 49 41 153 309
257 58 76 154 134
258 59 58 169 153
258 54 42 169 236
259 55 31 189 193

7. BAB II
PEMBAHASAN
1. a. Uji Asumsi
Uji Asumsi Normalitas
Tests of Normality
SUHU
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
DATA 15 .148 12 .200*
.949 12 .621
30 .152 12 .200*
.952 12 .664
45 .155 12 .200*
.962 12 .809
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Tests of Normality
JENIS
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
DATA bahan1 .260 12 .025 .910 12 .212
bahan2 .148 12 .200*
.966 12 .865
bahan3 .141 12 .200*
.965 12 .858
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.

8. Uji Normalitas
♦ H0 : data berdistribusi normal
H1 : data tidak berdistribusi normal
♦ Tingkat Signifikasi, α=0,05
♦ Statistik Uji
P_value bahan1 : 0,212
P_value bahan2 : 0,865
P_value bahan3 : 0,858
P_value suhu 15 : 0,621
P_value suhu 30 : 0,664
P_value suhu 45 : 0,809
♦ Daerah Kritik
H0 ditolak jika p_value < α (0,05)
♦ Kesimpulan
Karena p_value bahan1 ( 0,212 ) > α (0,05), bahan2 ( 0,865 ) > α (0,05), bahan3 (0,858 )
> α (0,05), suhu 15 ( 0,621 ) > α (0,05), suhu 30 ( 0,664 ) > α (0,05), dan suhu 45( 0,809 )
> α (0,05) maka H0 tidak ditolak. Jadi dapat disimpulkan bahwa data tersebut
berdistribusi normal
Uji Asumsi Kesamaan Variansi
Levene's Test of Equality of Error Variancesa
Dependent Variable:DATA
F df1 df2 Sig.
.902 8 27 .529
Tests the null hypothesis that the error variance of
the dependent variable is equal across groups.
a. Design: Intercept + SUHU + JENIS + SUHU * JENIS

9. Uji Hipotesis
♦ H0 : σ1=σ2=σ3 ( variansi semua data sama )
H1 : tidak semua variansi data sama
♦ Tingkat Signifikasi, α = 0,05
♦ Statistik Uji
P_value=0,529
F = 0,902
♦ Daerah Kritik
H0 ditolak jika p-value<α atau F>F(0,05;8;27)
♦ Kesimpulan
Dikarenakan p_value(0,529)>α(0,05) dan F(0,902)< F(0,05;8;27)(2,31) maka H0 tidak ditolak.
Sehingga dapat disimpulkan bahwa σ1=σ2=σ3 atau variansi data sama.
Dari output bisa terlihat bahwa dengan F hitung 0.902 , df(degree of freedom) 27 dan p_value 0.529
maka Ho dari asumsi pun tidak ditolak yang menyimpulkan variansi dari data sama.
b. Uji Interaksi

10. Uji Hipotesis
♦ H0 : tidak ada interaksi antara suhu dan jenis
H1 : ada interaksi antara suhu dan jenis
♦ Tingkat signifikasi, α=0,05
♦ Statistik Uji
P_value = 0,019
♦ Daerah Kritik
H0 ditolak jika p-value<α
♦ Kesimpulan
Dikarenakan p_value (0,019) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan
bahwa ada interaksi antara merk dan waktu. Untuk itu tidak dapat dilakukan uji efek
faktor.
Tests of Between-Subjects Effects
Dependent Variable:DATA
Source
Type III Sum of
Squares df Mean Square F Sig. Partial Eta Squared
Corrected Model 59416.222a
8 7427.028 11.000 .000 .765
Intercept 400900.028 1 400900.028 593.739 .000 .957
SUHU 39118.722 2 19559.361 28.968 .000 .682
JENIS 10683.722 2 5341.861 7.911 .002 .369
SUHU * JENIS 9613.778 4 2403.444 3.560 .019 .345
Error 18230.750 27 675.213
Total 478547.000 36
Corrected Total 77646.972 35
a. R Squared = .765 (Adjusted R Squared = .696)

11. c. Uji Multiple Comparison Analysis
Karena adanya interaksi dari kedua factor yakni suhu dan jenis bahan maka uji efek
factor tidak dapat dilakukan dan berdampak pula pada uji MCA yang tidak bisa dilakukan tanpa
adanya uji efek factor tersebut. Sehingga pertanyaan no 1 bagian c ini tidak bisa dijawab.
2.
a. Uji yang digunakan adalah uji Independensi karena di dalam soal, sampel yang
diambil adalah dari satu populasi yaitu mahasiswa yang diambil sampel sebanyak 160
mahasiswa dengan cara acak (random). Selain itu N total telah ditentukan dalam soal. Dan
penelitian diatas digunakan untuk mengetahui pengaruh perbedaan generasi dosen pengajar
dengan standar penilaian mata kuliah yang diajarkan.
b. Uji Independensi
dosen * nilai Crosstabulation
nilai
Totalburuk baik
dosen tua Count 31 49 80
Expected Count 24,5 55,5 80,0
muda Count 18 62 80
Expected Count 24,5 55,5 80,0
Total Count 49 111 160
Expected Count 49,0 111,0 160,0

12. Berdasarkan output di atas bisa dilihat bahwa expected count untuk dosen tua yang memberi
nilai buruk sebesar 24.5, expected count untuk dosen tua yang memberi nilai baik adalah
sebesar 55.5 dan total dosen tua adalah 80. Sedangkan untuk expected count untuk dosen
muda yang memberi nilai buruk adalah 24,5 dan expected count untuk dosen muda yang
memberi nilai baik sebesar 55,5. Sehingga untuk standar penilaian, untuk total expected count
untuk nilai buruk adalah 49 dan total untuk yang nilai baik adalah 111. Karena nilai expeted
count dari semuanya lebih dari 5 maka dalam uji hipotesis menggunakan p_value dari Pearson
Chi-Square dari tabel output Chi-Square Tests berikut:
Chi-Square Tests
Value df
Asymp. Sig. (2-
sided)
Exact Sig. (2-
sided)
Exact Sig. (1-
sided)
Pearson Chi-Square 4,972(b) 1 ,026
Continuity Correction(a) 4,236 1 ,040
Likelihood Ratio 5,017 1 ,025
Fisher's Exact Test ,039 ,020
Linear-by-Linear
Association
4,940 1 ,026
N of Valid Cases 160
a Computed only for a 2x2 table
b 0 cells (,0%) have expected count less than 5. The minimum expected count is 24,50.
Uji Hipotesis
♦ H0 : dosen independen terhadap standar penilaian ( tidak ada hubungan antara dosen
dengan standar penilaian )
H1 : dosen tidak independen terhadap standar penilaian (ada hubungan antara dosen
dengan standar penilaian )
♦ Tingkat signifikasi, α = 0,05
♦ Statistik Uji
P_value = 0,026
♦ Daerah Kritik

13. H0 ditolak jika p-value < α ( 0,05 )
♦ Kesimpulan
Karena p_value ( 0,026 ) < α ( 0,05 ) maka H0 ditolak. Sehingga dapat disimpulkan bahwa
dosen tidak independen dengan standar penilaian atau ada hubungan antara dosen
dengan standar penilaian. Maka untuk mengetahui keeratan hubungan antara dosen
dengan standar penilaian dapat diketahui melalui besarnya Odds Rasio ( OR ).
c. Dalam uji independensi diperlukan nilai OR ( Odds Rasio )
Risk Estimate
Value
95% Confidence Interval
Upper Lower
Odds Ratio for dosen
(tua / muda)
2,179 1,092 4,350
For cohort nilai = buruk 1,722 1,054 2,815
For cohort nilai = baik ,790 ,640 ,976
N of Valid Cases 160
Berdasarkan output di atas dapat dilihat bahwa besarnya Odds Rasio ( OR ) adalah 2.179,
artinya bahwa dosen tua yang menyatakan memberi nilai buruk 2,179 kali lipat lebih tinggi
dibandingkan dengan dosen muda yang memberi nilai baik.

14. 3.
Uji Asumsi
Tests of Normality
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
Kolesterol .127 80 .003 .925 80 .000
Umur .101 80 .042 .956 80 .008
HDL .075 80 .200*
.965 80 .026
LDL .099 80 .049 .971 80 .067
Trygliceride .154 80 .000 .836 80 .000
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Uji Normalitas
♦ H0 : data berdistribusi normal
H1 : data tidak berdistribusi normal
♦ Tingkat Signifikasi, α: 0,05
♦ Statistik Uji
p-value = 0,003
• Daerah kritik
H0 ditolak jika p-value < α
• Kesimpulan
Karena p-value (0,000) < α (0,05) maka H0 ditolak, sehingga data tidak berdistribusi
normal. Tetapi dalam kasus ini data diasumsikan berdistribusi normal.

15. TryglicerideLDLHDLumurkolesterol
TryglicerideLDLHDLumurkolesterol
Dari bagan matrix diatas bisa terlihat jelas bahwa sem ua factor saling berhubungan linear.Dikatakan
berhubungan linear karena setiap titik-titik yang ada pada matrik berada pada sekitar garis yang ada
pada matriks. Hal ini yang menandakan data tersebut berhubungan linear.
REGRESI PERTAMA
Model Summaryb
Model R R Square Adjusted R Square
Std. Error of the
Estimate
1 .993a
.986 .985 4.72883
a. Predictors: (Constant), Trygliceride, LDL, HDL, Umur
b. Dependent Variable: Kolesterol

16. MODEL SUMMARY
R = besar hubungan/ korelasi antara variabel adalah sebesar 0,993 atau 99,3%
R Square = 0,986 atau 98,6 %, variasi dalam variabel T dapat diterangkan oleh variabel X1 dan
sebesar 98,6 %
Adjusted R Square = besarnya koreksi terhadap R-Square adalah 0,985 atau 98,5 %
Standard Error = besarnya variasi dalam model sebesar 4,72883
ANOVAb
Model Sum of Squares df Mean Square F Sig.
1 Regression 115078.751 4 28769.688 1.287E3 .000a
Residual 1677.136 75 22.362
Total 116755.888 79
a. Predictors: (Constant), Trygliceride, LDL, HDL, Umur
b. Dependent Variable: Kolesterol
UJI OVERALL
H0 : Model regresi tidak layak digunakan
H1 : model regresi layak digunakan
Tingkat Signifikasi, α=0,05
Statistik Uji
p-value=0,000
Daerah Kritik
H0 ditolak jika p-value<α
Kesimpulan

17. Dikarenakan p-value (0,000)<α(0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa
model regresi layak digunakan.
Coefficientsa
Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig.B Std. Error Beta
1 (Constant) -2.990 3.877 -.771 .443
Umur .127 .071 .030 1.783 .079
HDL .988 .040 .371 24.439 .000
LDL 1.005 .018 .931 55.408 .000
Trygliceride .173 .006 .393 26.769 .000
a. Dependent Variable: Kolesterol
UJI PARSIAL
Constant
H0 : konstan tidak layak masuk dalam model
H1 : konstan layak masuk dalam model
Tingkat Signifikasi, α=0,05
Statistik Uji
p-value = 0,443
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,443) > α (0,05) maka H0 tidak ditolak. Sehingga dapat disimpulkan bahwa
konstan tidak layak masuk dalam model.

18. Variabel 1
H0 : variabel 1 tidak layak masuk dalam model
H1 : variabel 1 layak masuk dalam model
Tingkat Signifikasi, α = 0,05
Statistik Uji
p-value = 0,079
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,079) > α (0,05) maka H0 tidak ditolak. Sehingga dapat disimpulkan bahwa
variabel 1 tidak layak masuk dalam model.
Variabel 2
H0 : variabel 2 tidak layak masuk dalam model
H1 : variabel 2 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 2
layak masuk dalam model.
Variabel 3
H0 : variabel 3 tidak layak masuk dalam model
H1 : variabel 3 layak masuk dalam model

19. Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) > α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 3
layak masuk dalam model.
Variabel 4
H0 : variabel 4 tidak layak masuk dalam model
H1 : variabel 4 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 4
layak masuk dalam model.
Model belum layak digunakan karena masih adanya factor yang belum layak masuk dalam
model. Maka untuk melakukan regresi lagi factor yang tidak layak harus dikeluarkan
berdasarkan p_value paling tinggi terlenbih dahulu. Namun, pada permasalaahn ini constant
memiliki p_value paling besar. Hal ini pengecualian karena constant harus dikeluarkan terakhir
kali. Maka factor yang pertama kali dikeluarkan adalah variabel 1.
REGRESI KEDUA

20. Coefficientsa
Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig.B Std. Error Beta
1 (Constant) .436 3.416 .128 .899
HDL 1.006 .040 .377 25.308 .000
LDL 1.023 .015 .948 66.884 .000
Trygliceride .173 .007 .392 26.366 .000
a. Dependent Variable: Kolesterol
Uji Parsial
Constant
H0 : konstan tidak layak masuk dalam model
H1 : konstan layak masuk dalam model
Tingkat Signifikasi, α = 0,05
Statistik Uji
p-value = 0,899
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,899) > α (0,05) maka H0 tidak ditolak. Sehingga dapat disimpulkan bahwa
konstan tidak layak masuk dalam model.
Variabel 2
H0 : variabel 2 tidak layak masuk dalam model
H1 : variabel 2 layak masuk dalam model
Tingkat Signifikasi, α =0,05

21. Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 2
layak masuk dalam model.
Variabel 3
H0 : variabel 3 tidak layak masuk dalam model
H1 : variabel 3 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) > α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 3
layak masuk dalam model.
Variabel 4
H0 : variabel 4 tidak layak masuk dalam model
H1 : variabel 4 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
P_value = 0,000
Daerah Kritik

22. H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 4
layak masuk dalam model.
Pada regersi kedua constant masih belum layak dimasukkan kedalam model persamaan regresi.
Maka constant harus dikeluarkan dan dilakukan uji regresi ketiga.
REGRESI 3
Coefficientsa,b
Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig.B Std. Error Beta
1 HDL 1.010 .027 .237 37.428 .000
LDL 1.024 .011 .647 91.968 .000
Trygliceride .173 .005 .150 31.919 .000
a. Dependent Variable: Kolesterol
b. Linear Regression through the Origin
Uji Parsial
Variabel 2
H0 : variabel 2 tidak layak masuk dalam model
H1 : variabel 2 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000

23. Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 2
layak masuk dalam model.
Variabel 3
H0 : variabel 3 tidak layak masuk dalam model
H1 : variabel 3 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan
Karena p-value (0,000) > α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 3
layak masuk dalam model.
Variabel 4
H0 : variabel 4 tidak layak masuk dalam model
H1 : variabel 4 layak masuk dalam model
Tingkat Signifikasi, α =0,05
Statistik Uji
p-value = 0,000
Daerah Kritik
H0 ditolak jika p-value < α
Kesimpulan

24. Karena p-value (0,000) < α (0,05) maka H0 ditolak. Sehingga dapat disimpulkan bahwa variabel 4
layak masuk dalam model.
. Dan dari output di atas juga dihasilkan sebuah persamaan model regresi populasi yang sudah
baik digunakan :
Kolesterol=1,010*HDL+1,024*LDL+0,173*Trygliceride
Dari persamaan tersebut maka dapat disimpulkan bahwa setiap kenaikan 1 satuan variabel HDL
maka kolesterol naik sebesar 1,010 kali lipat HDL. Atau setiap kenaikan 1 satuan variabel LDL
maka kolesterol naik sebesar 1,024 kali lipat LDL, atau juga dapat disimpulkan bahwa setiap
kenaikan 1 satuan variabel Trygliceride maka kolesterol naik sebesar 0,173 kali lipat
Trygliceride.