Download as PDF, PPTX
Uploaded byAiko Matibag
L14
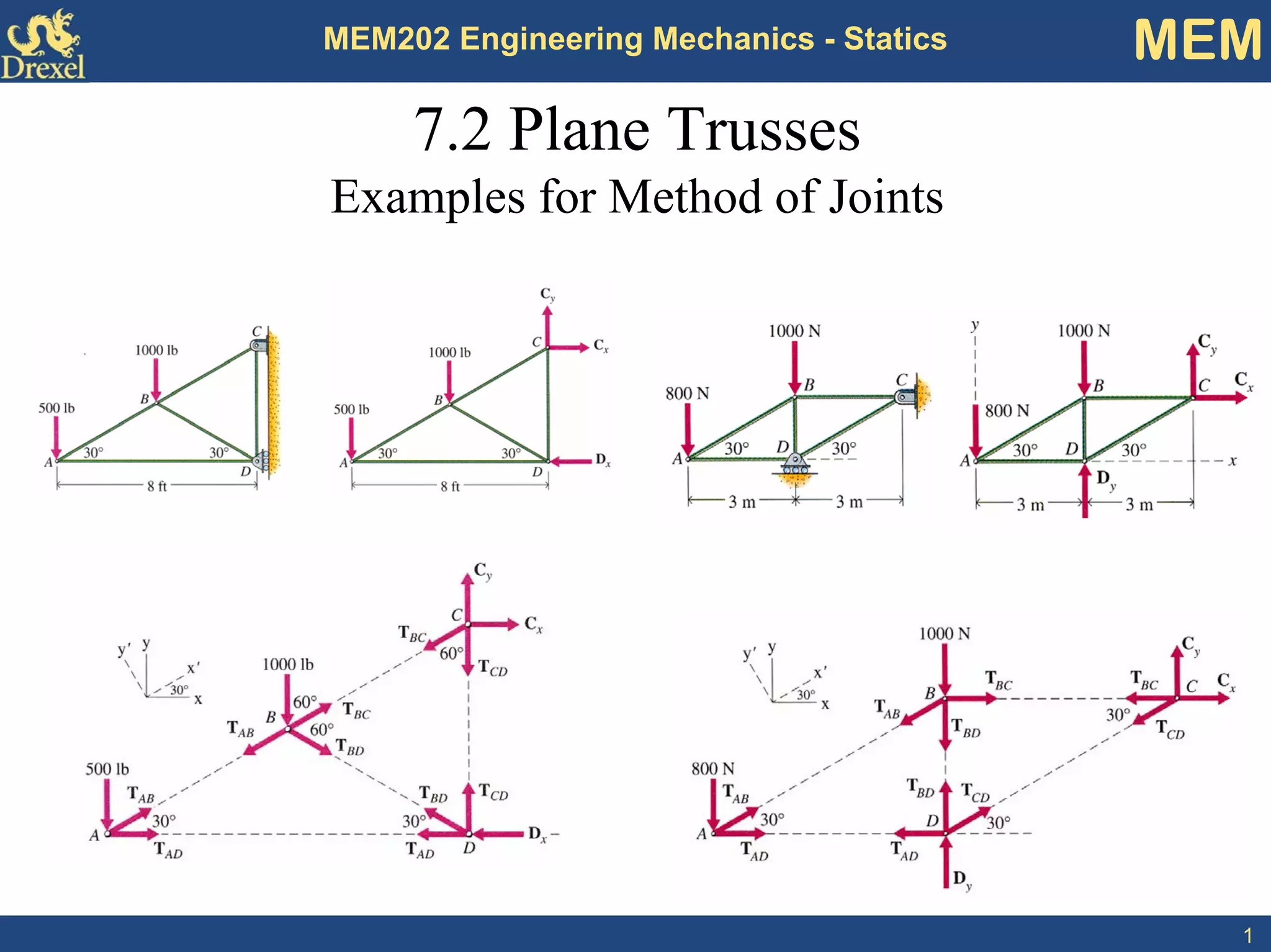
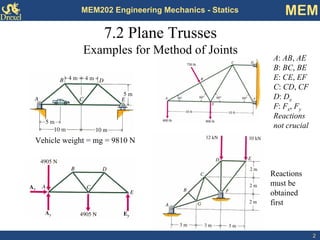
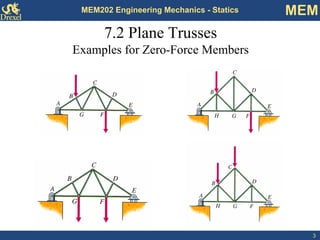
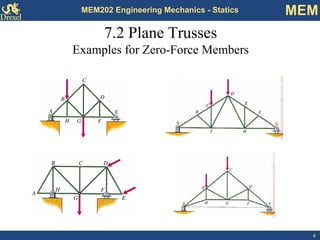
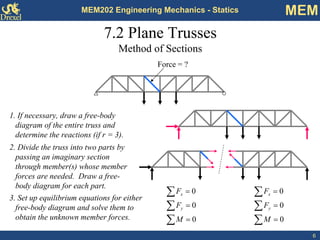
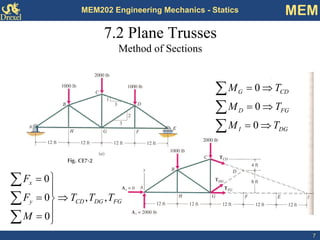
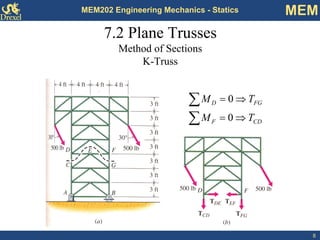
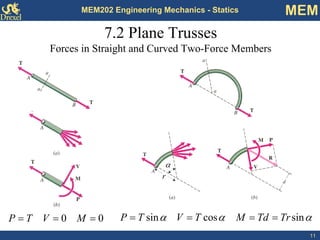
This document discusses methods for analyzing plane trusses, including the method of joints and method of sections. The method of joints is more convenient for simple trusses where all member forces are needed, while the method of sections is better for complex trusses where only a few member forces are required. The method of sections involves dividing the truss into parts with an imaginary cut and using equilibrium equations to solve for unknown member forces. An example of applying the method of sections to a space truss is also provided.
More Related Content
L14
- 1. 1 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Examples for Method of Joints
- 2. 2 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane TrussesExamples for Method of JointsVehicle weight = mg = 9810 N A: AB, AE B: BC, BE E: CE, EF C: CD, CF D: Dx F: Fx, Fy Reactions not crucial Reactions must be obtained first
- 3. 3 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Examples for Zero-Force Members
- 4. 4 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Examples for Zero-Force Members
- 5. 5 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Method of Sections Method of joints is more convenient when the truss is relatively simple and forces in all members are needed. 1F2F1R2RForce = ? Method of sections is more convenient when the truss is relatively complex and forces in only a few members are needed.
- 6. 6 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Method of SectionsForce = ? 1. If necessary, draw a free-body diagram of the entire truss and determine the reactions (if r = 3). 2. Divide the truss into two parts by passing an imaginary section through member(s) whose member forces are needed. Draw a free- body diagram for each part. 000= = = ΣΣΣ MFFyx000= = = ΣΣΣ MFFyx 3. Set up equilibrium equations for either free-body diagram and solve them to obtain the unknown member forces.
- 7. 7 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Method of SectionsDGIFGDCDGTMTMTM⇒= ⇒= ⇒= ΣΣΣ 000FGDGCDyxTTTMFF,, 000⇒ ⎪⎪⎭ ⎪⎪⎬ ⎫ = = = ΣΣΣ
- 8. 8 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Method of Sections K-TrussCDFFGDTMTM⇒= ⇒= ΣΣ 00
- 9. 9 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Method of SectionsBAECHFKINLOTRWUDGJMPSV Q Reactions at Aand B Section 1: AC, BESection 2: CF, EH Section 3: IF, HKSection 4: LI, KN cdef Joint V: VL, VTJoint W: WN, WU Joint R: RO, RTJoint S: SQ, SU Joint T: TL, TOJoint U: UN, UQ Joint O: OL, OPJoint Q: QN, QP Joint P: PL, PNJoint L: LM Joint N: NMJoint M: MI, MK Joint I: IJJoint K: KJ Joint J: JF, JHJoint F: FG Joint H: HGJoint G: GC, GE Joint C: CDJoint D: DA, DB Joint A: ABJoint B: Check
- 10. 10 MEM202 EngineeringMechanics - Statics MEM 7.3 Space Trusses2222222222223213232132323223232323++ −+− = ++ −−− = = + −− = + − = + + = kjiTFkjiTFjTFkiTFjiTFjiTFCDCDBDBDBCBCADADACACABABrrrrrrrrrrrrrrrrrrrkAjAiAAzyxrrrr++=kCjCCzyrrr+= kBBzrr= rjmjm−=−=3or 63()lb 30cos30sin125kjPrrroo−= 0=+++ADACABFFFArrrr0=+++BDDCABFFFBrrrr0=+++CDBCACFFFCrrrr0=+++CDBDADFFFPrrrr
- 11. 11 MEM202 EngineeringMechanics - Statics MEM 7.2 Plane Trusses Forces in Straight and Curved Two-Force Members α r αααsincossinTrTdMTVTP====00===MVTP