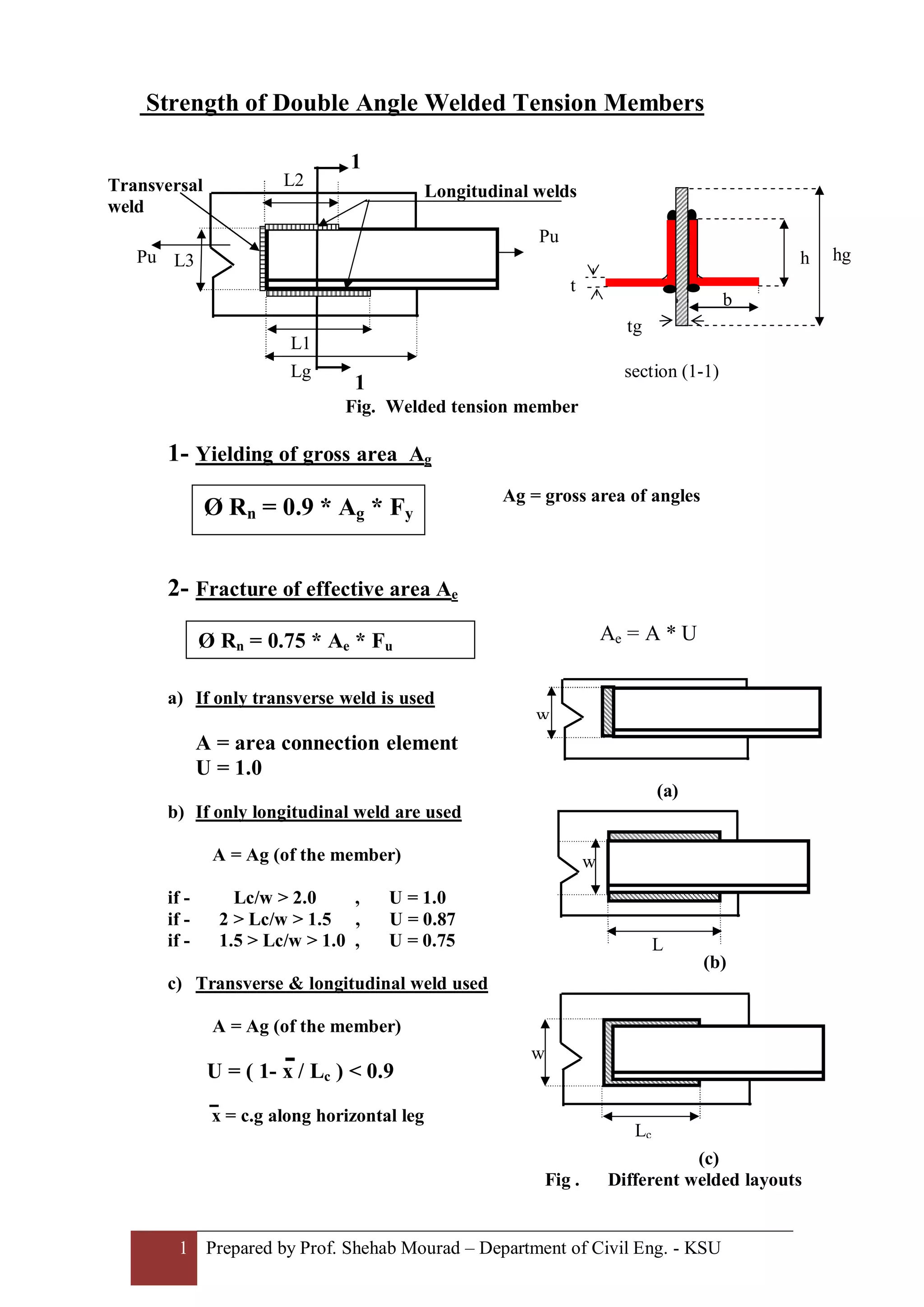
1. The document discusses the strength of double angle welded tension members. It describes three failure modes: yielding of the gross area, fracture of the effective area, and block shear rupture in the angle. 2. Formulas are provided to calculate the nominal resistance (Rn) for each failure mode based on the yield strength, ultimate tensile strength, and dimensions of the angles. 3. An example problem is worked through to determine the governing strength of a specific welded double angle configuration based on the provided dimensions and material properties. The yielding of the gross area controls with a nominal resistance of 459 kN.

1. 1 Prepared by Prof. Shehab Mourad – Department of Civil Eng. - KSU
Strength of Double Angle Welded Tension Members
Fig. Welded tension member
1- Yielding of gross area Ag
2- Fracture of effective area Ae
a) If only transverse weld is used
A = area connection element
U = 1.0
(a)
b) If only longitudinal weld are used
A = Ag (of the member)
if - Lc/w > 2.0 , U = 1.0
if - 2 > Lc/w > 1.5 , U = 0.87
if - 1.5 > Lc/w > 1.0 , U = 0.75
(b)
c) Transverse & longitudinal weld used
A = Ag (of the member)
U = ( 1- x / Lc ) < 0.9
x = c.g along horizontal leg
(c)
Fig . Different welded layouts
w
Lc
w
b
t
h hg
tg
section (1-1)
Pu
Pu
1
1
L2
L1
Lg
L3
Longitudinal weldsTransversal
weld
Ø Rn = 0.9 * Ag * Fy
Ø Rn = 0.75 * Ae * Fu
L
w
Ag = gross area of angles
Ae = A * U

2. 2 Prepared by Prof. Shehab Mourad – Department of Civil Eng. - KSU
3) Block shear rupture in angle
Fig. Block shear failure of welded angle
Lv = L1 , Lt = h - tangle
Av = 2 * tangle * Lv , At = 2 * tangle * Lt
At = gross area of tensile plane
Av = gross area of shear plane
Fu = Ultimate Tensile Strength of angles
Fy = Yield Tensile Strength of angles
Lt
Lv
If 0.6 * Fu * Av > Fu * At Ø Rn = 0.75 *(0.6 * Fu * Av + Fy * At)
If 0.6 * Fu * Av < Fu * At Ø Rn = 0.75 *( Fu * At + 0.6 * Fy * Av)

3. 3 Prepared by Prof. Shehab Mourad – Department of Civil Eng. - KSU
Example
Determine the factor tensile resistance of the given welded double
angles
Fig. Welded tension member for example
Given :
Fy = 250 MPa
Fu = 400 MPa
Solution
1- Yielding of Ag.
Ag = 2 * 1020 = 2040 mm2
Ø Rn = 0.9 * Fy * (2*Ag) = 0.9 * 250 * 2040 / 1000 = 459 kN
2- Fracture on Ae.
Ae = Ag*U
U = ( 1 – x / Lc) < 0.9
Lc = L1 = 114 mm
U = ( 1 – 19.8 / 114) = 0.826 < 0.90
Ø Rn = 0.75 * Ae * Fu = 0.75 * (2040*0.826) *400 / 1000 = 505.7 kN
3- Block shear rupture.
Therefore the governing strength of welded angles is given by
yielding of gross area = 459 kN
t
b
h hg
tg
section (1-1)
Lv
Lt
2L 89 x 76 x 6.4 mm
for single angle
Ag = 1020 mm2
x' = 19.8 mm
y' = 26.2 mm
Pu
Pu
1
1
L2
L1
Lg
L3
Longitudinal weldsTransversal
weld
L1 = 114 mm
L2 = 38 mm
L3 = 89 mm
Lv = L1 = 114 mm
Av = Lv * t = 114 * 2 * 6.4 = 1459.2 mm2
Lt = leg – t = 89 – 6.4 = 82.6 mm
At = 82.6 * 2 * 6.4 = 1057.28 mm2
Fu*At = 400 * 1057.28 = 422912 N
0.6* Fu *Av = 0.6 * 400 * 1459.2 = 350208 N < Fu*At
Ø Rn = 0.75*(422912+ 0.6*250*1459.2)/1000 = 481.3 kN