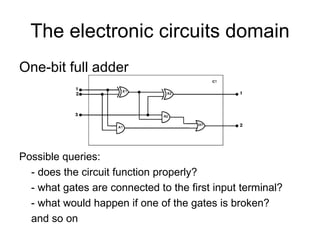
The document summarizes knowledge representation using first-order logic. It discusses several domains that can be represented including kinship relationships, mathematical sets, and the Wumpus world. It provides examples of how each domain can be encoded using predicates, functions, constants, assertions, and queries. Diagnostic and causal rules are explained for representing properties and deducing hidden attributes. The process of knowledge engineering is outlined including identifying the task, assembling relevant knowledge, and encoding the specific problem to pose queries and debug the knowledge base.

1. Knowledge Representation
using First-Order Logic

2. Domain
• Domain is a section of the knowledge
representation.
- The Kinship domain
- Mathematical sets
- Assertions and queries in first order logic
- The Wumpus World

3. Kinship domain

4. Kinship domain(family relationship)
It consists of
• Object – People
• Unary Predicates - Male and Female
• Binary Predicates - Parent,Brother,Sister
• Functions – Father, Mother
• Relations – Brotherhood, sisterhood.

5. Examples
The kinship domain:
• Brothers are siblings
∀x,y Brother(x,y) => Sibling(x,y)
• Male and female are disjoint categories
∀x, Male(x) ⇔ ¬Female(x)
• Parent and child are inverse relations
∀p,c Parent(p,c) ⇔ Child(c,p)

6. Mathematical sets

7. Mathematical set representation
• Constant – Empty set (s = {})
• Predicate – Member and subset (s1 ⊆ s2)
• Functions – Intersection( ∩ ) and union (∪ )
• Example: Two sets are equal if and only if each is a subset of the
other.
∀s1,s2 (s1=s2) ⇔(subset(s1,s2) ∧ subset(s2,s1))
Other eg:
∀x,s1,s2 x ∈ (s1 ∩ s2) ⇔ (x ∈ s1 ∧ x ∈ s2)
∀x,s1,s2 x ∈ (s1 ∪ s2) ⇔ (x ∈ s1 ∨ x ∈ s2)

8. Assertions and Queries in
first-order logic

9. Assertions
• Sentences are added to a knowledge base
using TELL are called assertions.
• We want to TELL things to the KB,
e.g. TELL(KB, King(John))
TELL(KB, ∀ x king(x) => Person(x))
John is a king and that king is a person.

10. Queries
• Questions are asked to the knowledge base
using ASK called as queries or goals.
• We also want to ASK things to the KB,
ASK(KB, ∃x , Person (x ) )
returns true by substituting john to a x.

11. Wumpus world

12. Agent Architectures
• Reflex agents: Classify their percept and act
accordingly.
• Model based agents: Construct an internal
representation of the world and use it to act.
• Goal based agent : Form goals and try to
achieve them.

13. FOL Version of Wumpus World
• Typical percept sentence:
Percept([Stench,Breeze,Glitter,None,None],3)
• In this sentence:
Percept - predicate
Stench, Breeze and glitter – Constants
3 – Integer to represent time
• Actions:
Turn Right), Turn Left), Forward, Shoot, Grab, Release,
Climb

14. Cont..,
• To determine best action, construct query:
∀ a BestAction(a,5)
• ASK solves this query and returns {a/Grab}
– Agent program then calls TELL to record the action
which was taken to update the KB.

15. • Percept sequences
1. Synchronic sentences (same time).
- sentences dealing with time.
2. Diachronic sentences (across time).
- agent needs to know how to
combine information about its previous
location to current location.

16. Two kinds of synchronic rules
1.Diagnostic rules
2.Casual rules

17. Deducing hidden properties
• Squares are breezy near a pit:
– Diagnostic rule---infer cause from effect
∀s Breezy(s) ⇔ ∃ r Adjacent(r,s) ∧ Pit(r)
– Causal rule---infer effect from cause
∀r Pit(r) ⇒ [∀s Adjacent(r,s) ⇒ Breezy(s)]

18. Knowledge engineering in
FOL

19. Steps
1. Identify the task
3. Assemble the relevant knowledge
5. Decide on a vocabulary of predicates, functions, and
constants
7. Encode general knowledge about the domain
9. Encode a description of the specific problem instance
11. Pose queries to the inference procedure and get
answers
13. Debug the knowledge base

20. The electronic circuits domain
One-bit full adder
Possible queries:
- does the circuit function properly?
- what gates are connected to the first input terminal?
- what would happen if one of the gates is broken?
and so on

21. The electronic circuits domain
1. Identify the task
– Does the circuit actually add properly?
2. Assemble the relevant knowledge
– Composed of wires and gates; Types of gates (AND,
OR, XOR, NOT)
– Two input terminals and one output terminal

22. 3. Decide on a vocabulary
• Alternatives:
Type(X1) = XOR (function)
Type(X1, XOR) (binary predicate)
XOR(X1) (unary predicate)
It can be represented by either
binary predicate or individual type.

23. 4. Encode general knowledge of the
domain
1.If two terminals are connected, then they have
the same signal.
∀t1,t2 Connected(t1, t2) ⇒ Signal(t1) = Signal(t2)
2.The signal at every terminal is either 1 or 0
(but not both)
∀t Signal(t) = 1 ∨ Signal(t) = 0
1≠0

24. 3. Connected is a commutative predicate.
∀t1,t2 Connected(t1, t2) ⇒ Connected(t2, t1)
4. An OR gate’s output is 1 if and only if any of its input is 1.
∀g Type(g) = OR ⇒
Signal(Out(1,g)) = 1 ⇔ ∃n Signal(In(n,g)) = 1

25. 5. An AND gate’s output is 0 if and only if any of its
input is 0.
∀g Type(g) = AND ⇒
Signal(Out(1,g)) = 0 ⇔ ∃n Signal(In(n,g)) = 0
6. An XOR gate’s output is 1 if and only if any of its
inputs are different:
∀g Type(g) = XOR ⇒Signal(Out(1,g)) = 1 ⇔
Signal(In(1,g)) ≠ Signal(In(2,g))

26. 7. An XOR gate’s output is 1 if and only if any of its
inputs are different:
∀g Type(g) = NOT ⇒
Signal(Out(1,g)) ≠ Signal(In(1,g))

27. 5. Encode the specific problem
instance
• First we categorize the gates:
Type(X1) = XOR Type(X2) = XOR
Type(A1) = AND Type(A2) = AND
Type(O1) = OR
– Then show the connections between them:

28. Connected(Out(1,X1),In(1,X2))
Connected(In(1,C1),In(1,X1))
Connected(Out(1,X1),In(2,A2))
Connected(In(1,C1),In(1,A1))
Connected(Out(1,A2),In(1,O1))
Connected(In(2,C1),In(2,X1))
Connected(Out(1,A1),In(2,O1))
Connected(In(2,C1),In(2,A1))
Connected(Out(1,X2),Out(1,C1))
Connected(In(3,C1),In(2,X2))
Connected(Out(1,O1),Out(2,C1))
Connected(In(3,C1),In(1,A2))

29. 6. Pose queries to the inference
procedure and get answers
For the given query the inference
procedure operate on the problem
specific facts and derive the answers.

30. What are the possible sets of values of all the
terminals for the adder circuit?
∃i1,i2,i3,o1,o2 Signal(In(1,C1)) =
i1 ∧ Signal(In(2,C1)) = i2 ∧ Signal(In(3,C1)) = i3 ∧
Signal(Out(1,C1)) = o1 ∧ Signal(Out(2,C1)) = o2

31. 7. Debug the knowledge base
• For the given query, if the result is not a
user expected one then KB is updated
with relevant axioms.
• The KB is checked with different
constraints.eg:prove any output for the
circuit i.e.,0 or 1.