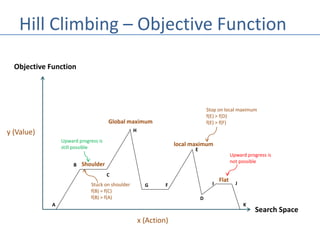
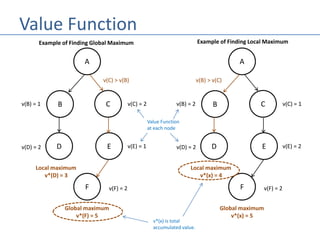
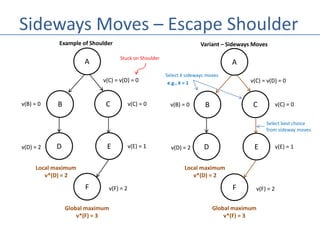
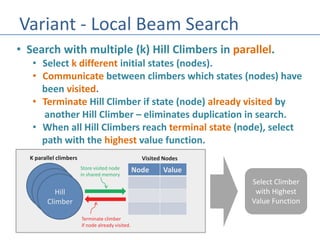
The document describes the hill climbing algorithm, a local search method that selects the best immediate choice to find an optimal solution while ignoring past steps and current solution optimality. It explains the algorithm's process, including defining an evaluation function, selecting actions based on their value, and variations like sideways moves and stochastic approaches. It also introduces local beam search, which utilizes multiple hill climbers to enhance the search process by avoiding duplication of visited states.

1. Artificial Intelligence
Hill Climbing and Local Search
Portland Data Science Group
Created by Andrew Ferlitsch
Community Outreach Officer
July, 2017

2. Hill Climbing Algorithm
• A search method of selecting the best local choice at
each step in hopes of finding an optimal solution.
• Does not consider how optimal the current solution is.
• Does not consider steps past the next immediate choice.
• Steps:
1. Define an evaluation function f(x) to determine the
value of a state.
2. From the current state, determine the search space
(actions) for one step ahead.
3. Select the action from the search space that returns the
highest value.

3. Hill Climbing – Objective Function
x (Action)
y (Value)
Global maximum
local maximum
Shoulder
Search Space
Objective Function
Stuck on shoulder
f(B) = f(C)
f(B) > f(A)
A
B
C
D
E
F
Stop on local maximum
f(E) > f(D)
f(E) > f(F)
G
H
Flat
I J
K
Upward progress is
still possible
Upward progress is
not possible

4. Value Function
A
B
E
C
D
v(B) = 1 v(C) = 2
v(E) = 1v(D) = 2
F v(F) = 2
Global maximum
v*(F) = 5
Local maximum
v*(D) = 3
A
B
E
C
D
v(B) = 2 v(C) = 1
v(E) = 2v(D) = 2
F v(F) = 2
Global maximum
v*(x) = 5
Local maximum
v*(x) = 4
v(C) > v(B)
Example of Finding Global Maximum Example of Finding Local Maximum
Value Function
at each node
v*(x) is total
accumulated value.
v(B) > v(C)

5. Algorithm
function HillClimb( initial )
initialize node with initial # set the current node to the starting point
while forever # continue until you cannot climb higher
initialize max to minus infinity # minimum value
for each child (neighbor) of the node
if v(child) > max # find neighbor with max value
max = v(child)
next = child
if max <= 0 # cannot climb higher
return node
node = next # climb to the next node

6. Sideways Moves – Escape Shoulder
A
B
E
C
D
v(B) = 0 v(C) = 0
v(E) = 1v(D) = 2
F v(F) = 2
Global maximum
v*(F) = 3
Local maximum
v*(D) = 2
v(C) = v(D) = 0
Example of Shoulder
Stuck on Shoulder
Variant – Sideways Moves
A
B
E
C
D
v(B) = 0 v(C) = 0
v(E) = 1v(D) = 2
F v(F) = 2
Global maximum
v*(F) = 3
Local maximum
v*(D) = 2
v(C) = v(D) = 0
Select k sideways moves
e.g., k = 1
Select best choice
from sideway moves

7. Algorithm – Sideways Moves
function HillClimb( initial, k )
initialize node with initial # set the current node to the starting point
while forever # continue until you cannot climb higher
initialize max to minus infinity # minimum value
for each child (neighbor) of the node
if v(child) > max # find neighbor with max value
max = v(child)
next = child
if max <= 0 # cannot climb higher
if k == 0
return node
for each child (neighbor) of the node
value = HillClimb( child, k-1)
if value > max
max = value
next = child
if max <= 0
return node
node = next # climb to the next node
Add parameter for number of sideways moves
No sideways moves
Recursively call the HillClimb
algorithm on each child, while
decrementing the number of
sideways moves (depth)
Decrease k by one

8. Variant - Stochastic
• Stochastic – choose node at random
• If none of the child (neighbor) nodes has a value > 0,
then choose one of the nodes at random.
• There needs to be a cutoff (k) of random choices, or the
method will go into an infinite loop (e.g., you are at the
global maximum).

9. Variant - Local Beam Search
Hill
Climber
Hill
Climber
Hill
Climber
• Search with multiple (k) Hill Climbers in parallel.
• Select k different initial states (nodes).
• Communicate between climbers which states (nodes) have
been visited.
• Terminate Hill Climber if state (node) already visited by
another Hill Climber – eliminates duplication in search.
• When all Hill Climbers reach terminal state (node), select
path with the highest value function.
Node Value
Visited NodesK parallel climbers
Terminate climber
if node already visited.
Store visited node
in shared memory
Select Climber
with Highest
Value Function