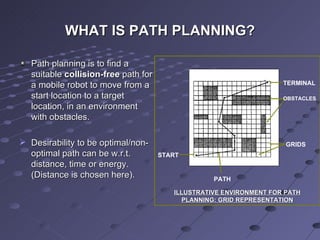
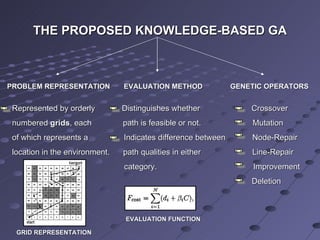
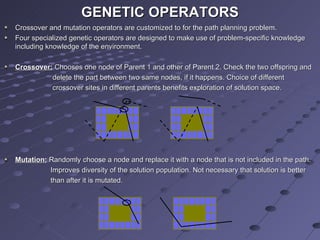
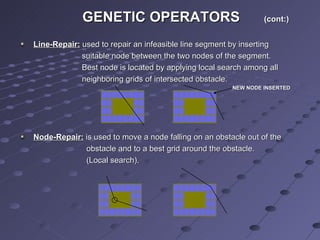
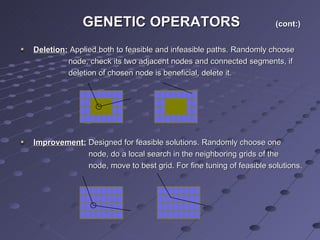
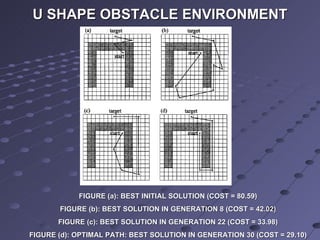
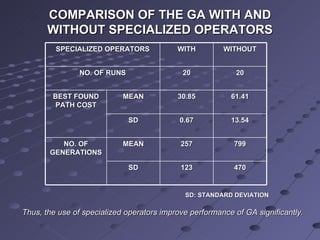
This document summarizes a research paper that proposes a knowledge-based genetic algorithm for mobile robot path planning. The algorithm uses a grid-based representation and specialized genetic operators informed by domain knowledge. Simulation results show the algorithm can find optimal or near-optimal paths in static and dynamic environments. Comparisons demonstrate the specialized operators improve GA performance over standard operators. Future work could better utilize domain knowledge and handle changes in dynamic environments.

1. A KNOWLEDGE BASED GENETIC ALGORITHM FOR PATH PLANNING OF A MOBILE ROBOT Presented by: Tarundeep Dhot Dept of ECE Concordia University

2. This presentation is based on a research paper written by the following authors: Y. Hu and Simon Yang This paper was published at: International Conference of Robotics and Automation, New Orleans LA – April 2004 This presentation is solely meant for educational purposes. Acknowledgements

3. Salient Features Knowledge Based GA for PATH PLANNING for mobile robot proposed. Proposed GA incorporates domain knowledge into its specialized genetic operators (local search). Unique and simple path representation method . Simple but effective evaluation method . GA capable of finding optimal or near optimal robot path in both static as well as dynamic environments. Irreplaceable role of SPECIALIZED GENETIC OPERATORS demonstrated by comparison study.

4. WHAT IS PATH PLANNING? Path planning is to find a suitable collision-free path for a mobile robot to move from a start location to a target location, in an environment with obstacles. Desirability to be optimal/non-optimal path can be w.r.t. distance, time or energy. (Distance is chosen here). PATH START TERMINAL OBSTACLES GRIDS ILLUSTRATIVE ENVIRONMENT FOR PATH PLANNING: GRID REPRESENTATION

5. KNOWLEDGE-BASED GAs Preferred over Classical GAs. Use specialized genetic operators (apart from the usual two) and can have variable length binary strings. Knowledge incorporation essential in the path planning problem which improves the efficiency of the GAs as compared to the “blind” search made by Classical GAs.

6. THE PROPOSED KNOWLEDGE-BASED GA PROBLEM REPRESENTATION EVALUATION METHOD GENETIC OPERATORS Represented by orderly Distinguishes whether Crossover numbered grids , each path is feasible or not. Mutation of which represents a Indicates difference between Node-Repair location in the environment. path qualities in either Line-Repair category. Improvement Deletion GRID REPRESENTATION EVALUATION FUNCTION

7. PROBLEM REPRESENTATION Represented by orderly numbered grids (eg: 10 X 10), each of which represents a location in the environment. Boundary of obstacles is formed by their actual boundary plus minimum safety distance considering the size of the mobile robot (so that robot can be considered as a point in the environment). Encoding of path: Sequence of grid numbers from source to target with all the intermediate nodes. Length of chromosomes varies from 2 to N max MOBILE ROBOT ENVIRONMENT AND PATH REPRESENTATION. SOLID LINE: FEASIBLE PATH; DASHED LINE: INFEASIBLE PATH START TARGET START POINT 0 – 24 – 36 – 66 – 74 – 84 - 99 START POINT TARGET POINT NODE A SAMPLE CHROMOSOME: A PATH REPRESENTED BY NODES FALLING ON GRIDS WITH DIFFERENT NUMBERS

8. PROBLEM REPRESENTATION (cont:) A feasible path is a collision free path i.e. no nodes fall on any obstacle, or non of the line segments of a path intersects an obstacle.

9. EVALUATION METHOD Path can either be feasible (collision-free) or infeasible since intermediate nodes can fall on any grids. Evaluation should be able to distinguish between feasible and infeasible paths and also indicate difference of path qualities within either category. Evaluation Function: F cost = ∑ ( d i + β i C) for i=1 to N where: N = No. of line segments of a path d i = Euclidean distance of the two nodes forming line segment C = Constant β i = Coefficient denoting depth of collision. By definition: β i = 0 if the i th line segment is feasible. ∑ α j ; (j=1 to M) if the line segment intersects obstacle(s) where: M = No. of obstacles the line segment intersects. α j  Determined by how deep a line segment intersects an object j. Defined as shorted moving distance for escaping the intersected object.

10. EVALUATION METHOD (cont:) This evaluation gives penalty to infeasible paths but still keep them in population because they might become good feasible solutions after certain genetic transformations. Allows overlap between fitness of feasible and infeasible solutions because a very poor feasible path is not necessarily better than a very good near feasible path. Better chance for good infeasible solutions to evolve into a good solution. To save computational time, some information obtained by evaluation needs to be recorded so that later on it can be used by some specialized genetic operators as heuristic knowledge without re-calculation. ● Feasibility : Feasible/Infeasible, Node-infeasible/Line-infeasible. ● Number of infeasible nodes or line segments. ● Which obstacle(s) a path intersects.

11. GENETIC OPERATORS Crossover and mutation operators are customized to for the path planning problem. Four specialized genetic operators are designed to make use of problem-specific knowledge including knowledge of the environment. Crossover: Chooses one node of Parent 1 and other of Parent 2. Check the two offspring and delete the part between two same nodes, if it happens. Choice of different crossover sites in different parents benefits exploration of solution space. Mutation: Randomly choose a node and replace it with a node that is not included in the path. Improves diversity of the solution population. Not necessary that solution is better than after it is mutated.

12. GENETIC OPERATORS (cont:) Line-Repair: used to repair an infeasible line segment by inserting suitable node between the two nodes of the segment. Best node is located by applying local search among all neighboring grids of intersected obstacle. Node-Repair: is used to move a node falling on an obstacle out of the obstacle and to a best grid around the obstacle. (Local search). NEW NODE INSERTED

13. GENETIC OPERATORS (cont:) Deletion: Applied both to feasible and infeasible paths. Randomly choose node, check its two adjacent nodes and connected segments, if deletion of chosen node is beneficial, delete it. Improvement: Designed for feasible solutions. Randomly choose one node, do a local search in the neighboring grids of the node, move to best grid. For fine tuning of feasible solutions.

14. DYNAMIC ENVIRONMENT Suitable for dynamic environment i.e. if environment is changed. If environment is changed, the algorithm will re-evaluate the current population according to the new environment and starts the process to get a new solution. To increase diversity of the population, mutation with higher probability is applied to the current population.

15. SIMULATIONS Effectiveness of proposed GA demonstrated by simulations. Parameter settings: Population size = 50 Probability for mutation = 0.2/chromosome and 0.9 for rest. Tournament selection and elitism are applied. 16 X 16 grids applied to the environments. All simulations are done on a Pentium 3 PC. Simulation is specially important for three types of paths: Path Planning in an Environment with a U-Shaped Obstacle: With more number of generations, GA will evolve better solution, as shown in the figure. Path Planning in Complex Environment: GA applied to different mobile robot environments with different obstacle layouts. Path Planning in a Dynamic Environment: Proposed GA works well both with static as well as dynamic environments. When environment changes, information of obstacles is updated. The algorithm re-evaluates the current population according to new information. Cost of solution for current population are updated.

16. U SHAPE OBSTACLE ENVIRONMENT FIGURE (a): BEST INITIAL SOLUTION (COST = 80.59) FIGURE (b): BEST SOLUTION IN GENERATION 8 (COST = 42.02) FIGURE (c): BEST SOLUTION IN GENERATION 22 (COST = 33.98) FIGURE (d): OPTIMAL PATH: BEST SOLUTION IN GENERATION 30 (COST = 29.10)

17. PATH PLANNING IN COMPLEX ENVIRONMENT FIGURE (a): PATH OBTAINED BY GA IN ONE TYPICAL RUN FIGURE (b): THREE ALTERNATIVE PATHS OBTAINED BY GA FROM DIFFERENT RUNS

18. PATH PLANNING IN A DYNAMIC ENVIRONMENT FIGURE (a): PATH OBTAINED IN THE ORIGINAL ENVIRONMENT FIGURE (b): PATH AFTER ADDING OBSTACLE FIGURE (c): PATH AFTER REMOVAL OF THE OBSTACLE

19. COMPARISON OF THE GA WITH AND WITHOUT SPECIALIZED OPERATORS SD: STANDARD DEVIATION Thus, the use of specialized operators improve performance of GA significantly. SPECIALIZED OPERATORS WITH WITHOUT NO. OF RUNS 20 20 BEST FOUND PATH COST MEAN 30.85 61.41 SD 0.67 13.54 NO. OF GENERATIONS MEAN 257 799 SD 123 470

20. CONCLUSIONS: Knowledge-based GA proposed. Simple and effective path representation and evaluation. Domain knowledge is incorporated in the problem specific genetic operators. Statistical analysis show specialized operators improve performance of GA significantly. Effective both in complex static as well as dynamic environments. Future Work: Better utilization of domain knowledge esp to generate more feasible solutions for initial population. Since it deals with dynamic environments, new solutions based on knowledge about the environment change can be injected into the population.

21. THANK YOU !!