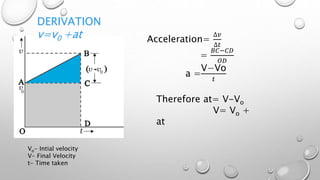
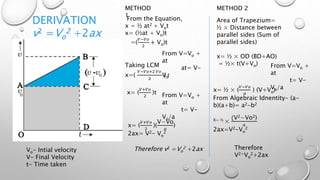
This document derives three equations for calculating displacement (x) from velocity-time graphs using different methods: 1) x = 1/2 at^2 + Vot 2) x = (V+Vo)/2 * t 3) x = 1/2 * (V^2 - Vo^2)/a Where Vo is the initial velocity, V is the final velocity, t is time, and a is acceleration. The derivations show calculating the area under the velocity-time graph in different ways to relate it to displacement.

2. Acceleration=
∆𝑣
∆𝑡
=
𝐵𝐶−𝐶𝐷
𝑂𝐷
a =
V−Vo
𝑡
DERIVATION
v=v0 +at
Therefore at= V-Vo
V= Vo +
at
Vo- Intial velocity
V- Final Velocity
t- Time taken

3. Area under the Graph =
Area of Rectangle ACDO + Area of
Triangle ABC
=L × B + ½ × l × b
= AO × OD + ½ × AC × BC
= Vo × t + ½ × t × (V-Vo)
As we have studied that
the area under v-t curve represents the
displacement. Therefore, the displacement x
of the object is :
x = ½ (V-Vo)t + V 𝑜t
But we know that , v−v0
=at
Therefore, x = ½ at2 + Vot
DERIVATION
x = ½ at2 + Vot
Vo- Intial velocity
V- Final Velocity
t- Time taken

4. DERIVATION
v2 =Vo
2 +2ax
From the Equation,
x = ½ at2 + Vot
x= (½at + Vo)t
=(
𝑉−𝑉𝑜
2
+ Vo)t
From V=Vo +
at
at= V-
Vo
Taking LCM
x=(
𝑉−𝑉𝑜+2 𝑉𝑜
2
) 𝑡
x= (
𝑉+𝑉𝑜
2
)t From V=Vo +
at
t= V-
Vo/a
x= (
𝑉+𝑉𝑜
2
)(
V−Vo
𝑎
)
2ax= V2- Vo
2
Therefore v2 =Vo
2 +2axVo- Intial velocity
V- Final Velocity
t- Time taken
Area of Trapezium=
½ × Distance between
parallel sides (Sum of
parallel sides)
x= ½ × OD (BD+AO)
= ½× t(V+Vo) From V=Vo +
at
t= V-
Vo/ax= ½ × (
𝑉−𝑉𝑜
𝑎
) (V+Vo)
From Algebraic Idnentity- (a-
b)(a+b)= a2-b2
X= ½ ×
(V2−Vo2)
𝑎
2ax=V2-Vo
2
Therefore
V2=Vo
2+2ax
METHOD
1
METHOD 2