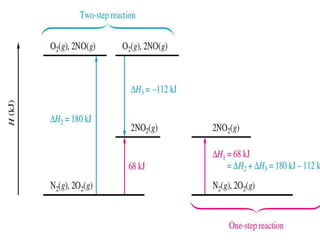
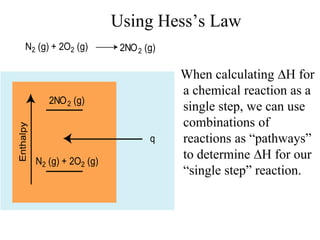
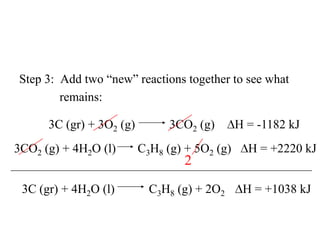Hess's law states that the enthalpy change of a reaction is independent of the pathway taken, as enthalpy is a state function. Using Hess's law, the enthalpy change of a reaction can be calculated by adding together enthalpy changes of multiple steps that combine to give the overall reaction. This is demonstrated with examples calculating the enthalpy change of reactions by combining known reaction enthalpies. Reactions can be reversed and coefficients adjusted as needed to achieve the desired overall reaction.

1. Lecture 4: Hess’s Law
Reading: Zumdahl 9.5
Outline:
Definition of Hess’ Law
Using Hess’ Law (examples)

2. Q: What is Hess’s Law ?
• Recall (lecture 3) Enthalpy is a state function.
As such, H for going from some initial state to
some final state is pathway independent.
• Hess’s Law: H for a process involving the
transformation of reactants into products is not
dependent on pathway.
(This means we can calculate H for a reaction by a
single step, or by multiple steps)

4. Using Hess’s Law
N2 (g) + 2O2 (g) 2NO 2 (g)
When calculating H for
a chemical reaction as a
2NO 2 (g)
single step, we can use
combinations of
q reactions as “pathways”
N2 (g) + 2O2 (g)
to determine H for our
“single step” reaction.

5. The reaction of interest is:
N2(g) + 2O2(g) 2NO2(g) H = 68 kJ
This reaction can also be carried out in two steps:
N2 (g) + O2 (g) 2NO(g) H = +180 kJ
2NO (g) + O2(g) 2NO2(g) H = -112 kJ

6. • If we take the previous two reactions and add
them, we get the original reaction of interest:
N2 (g) + O2 (g) 2NO(g) H = +180 kJ
2NO (g) + O2 (g) 2NO2(g) H = -112 kJ
N2 (g) + 2O2 (g) 2NO2(g) H = + 68 kJ

7. Note: the important things about this example is that
the sum of H for the two reaction steps is equal
to the H for the reaction of interest.
Big idea: We can combine reactions of known
H to determine the H for the
overall
“combined” reaction.

8. Hess’s Law: An Important Detail
One can always reverse the direction of a
reaction when making a combined reaction.
When you do this, the sign of H changes.
N2(g) + 2O2(g) 2NO2(g) H = +68 kJ
2NO2(g) N2(g) + 2O2(g) H = - 68 kJ

9. One more detail:
• The magnitude of H is directly proportional to the
quantities involved. (This means H is an “extensive”
quantity).
• So, if the coefficients of a reaction are multiplied by a
number, the value of H is also multiplied by the
same number.
N2(g) + 2O2(g) 2NO2(g) H = 68 kJ
N2(g) + 4O2(g) 4NO2(g) H = 136 kJ

10. Using Hess’s Law: tips
• When trying to combine reactions to form a
reaction of interest, it is usually best to work
backwards from the reaction of interest.
• Example:
What is H for the following reaction?
3C (gr) + 4H2 (g) C3H8 (g)

11. 3C (gr) + 4H2 (g) C3H8 (g) H=?
You’re given the following reactions:
C (gr) + O2 (g) CO2 (g) H = -394 kJ
C3H8 (g) + 5O2 (g) 3CO2 (g) + 4H2O (l) H = -2220 kJ
H2 (g) + 1/2O2 (g) H2O (l) H = -286 kJ

12. Step 1. Only reaction 1 has C (gr). Therefore, we
will multiply by 3 to get the correct amount of C
(gr) with respect to our final equation.
(x3) C (gr) + O2 (g) CO2 (g) H = -394 kJ
3C (gr) + 3O2 (g) 3CO2 (g) H = -1182 kJ

13. Step 2: To get C3H8 on the product side of the
reaction, we need to reverse reaction 2, and change
the sign of H.
C3H8 (g) + 5O2 (g) 3CO2 (g) + 4H2O (l) H = -2220 kJ
3CO2 (g) + 4H2O (l) C3H8 (g) + 5O2 (g) H = +2220 kJ

14. Step 3: Add two “new” reactions together to see what
remains:
3C (gr) + 3O2 (g) 3CO2 (g) H = -1182 kJ
3CO2 (g) + 4H2O (l) C3H8 (g) + 5O2 (g) H = +2220 kJ
2
3C (gr) + 4H2O (l) C3H8 (g) + 2O2 H = +1038 kJ

15. • Step 4: Compare previous reaction to final
reaction, and determine how to reach final
reaction:
3C (gr) + 4H2O (l) C3H8 (g) + 2O2 H = +1038 kJ
H2 (g) + 1/2O2 (g) H2O (l) H = -286 kJ
3C (gr) + 4H2 (g) C3H8 (g)
Need to multiply second reaction by 4

16. Example (cont.)
• Step 4: Compare previous reaction to final
reaction, and determine how to reach final
reaction:
3C (gr) + 4H2O (l) C3H8 (g) + 2O2 H = +1038 kJ
4H2 (g) + 2O2 (g) 4H2O (l) H = -1144 kJ
3C (gr) + 4H2 (g) C3H8 (g)

17. 3C (gr) + 4H2O (l) C3H8 (g) + 2O2 H = +1038 kJ
4H2 (g) + 2O2 (g) 4H2O (l) H = -1144 kJ
3C (gr) + 4H2 (g) C3H8 (g) H = -106 kJ
Which is the one step reaction of interest

18. Another Example:
• Calculate H for the following reaction:
H2(g) + Cl2(g) 2HCl(g)
Given the following:
NH3 (g) + HCl (g) NH4Cl(s) H = -176 kJ
N2 (g) + 3H2 (g) 2NH3 (g) H = - 92 kJ
N2 (g) + 4H2 (g) + Cl2 (g) 2NH4Cl(s) H = - 629 kJ

19. Step 1: Only the first reaction contains the product
of interest (HCl), but as a reactant.
Therefore, reverse this reaction and multiply by 2
to get stoichiometry correct.
NH3 (g) + HCl (g) NH4Cl(s) H = -176 kJ
2NH4Cl(s) 2NH3 (g) + 2HCl (g) H = +352 kJ

20. Step 2: Need Cl2 as a reactant, therefore, add
reaction 3 to result from step 1 and see what is
left.
2NH4Cl(s) 2NH3 (g) + 2HCl (g) H = 352 kJ
N2(g) + 4H2(g) + Cl2(g) 2NH4Cl(s) H = -629 kJ
N2 (g) + 4H2 (g) + Cl2 (g) 2NH3(g) + 2HCl(g)
H = -277 kJ

21. Step 3: Use remaining known reaction in
combination with the result from Step 2 to get
final reaction.
N2 (g) + 4H2 (g) + Cl2 (g) 2NH3(g) + 2HCl(g) H = -277 kJ
? ( N2 (g) + 3H2(g) 2NH3(g) H = -92 kJ)
H2(g) + Cl2(g) 2HCl(g) H=?
Key: need to reverse the middle reaction

22. • Step 3. Use remaining known reaction in
combination with the result from Step 2 to
get final reaction.
N2 (g) + 4H2 (g) + Cl2 (g) 2NH3(g) + 2HCl(g) H = -277 kJ
1
2NH3(g) 3H2 (g) + N2 (g) H = +92 kJ
H2(g) + Cl2(g) 2HCl(g) H = -185 kJ
This is the desired reaction and resultant H!