Downloaded 1,376 times
Uploaded byKelvin Stott
Understanding Risk & Uncertainty
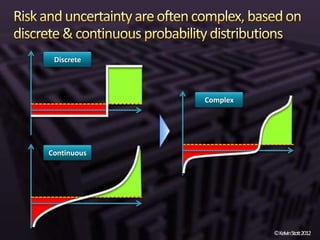
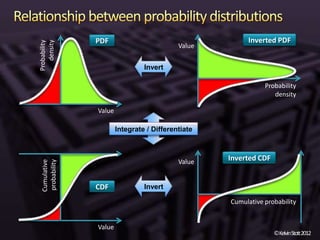
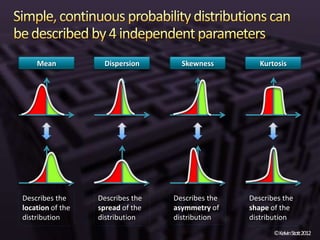
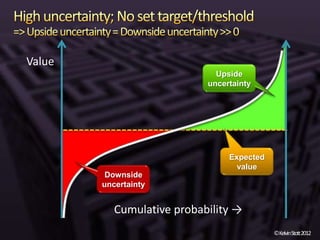
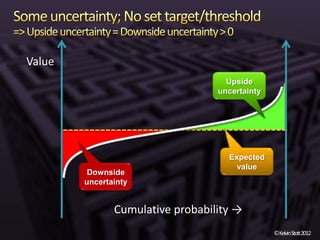
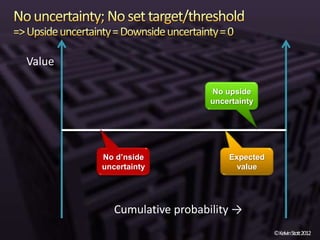
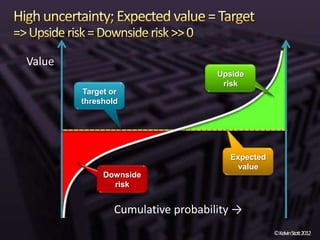
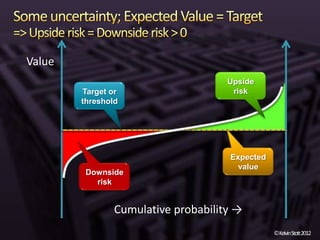
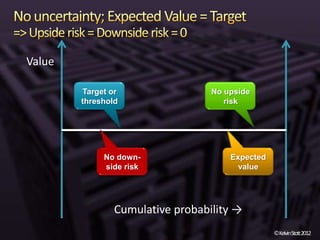
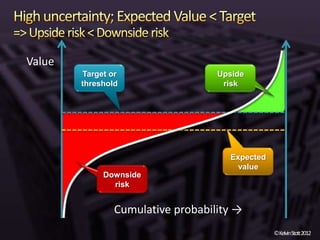
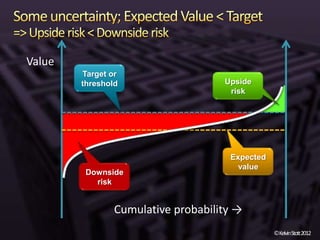
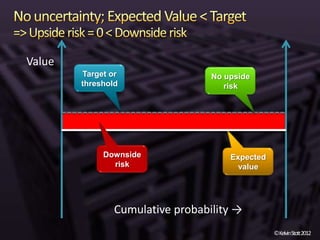
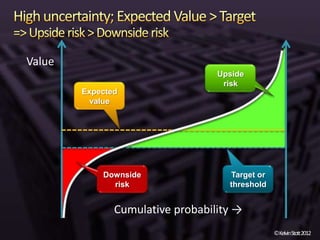
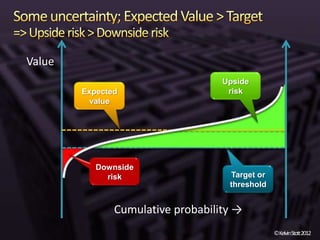
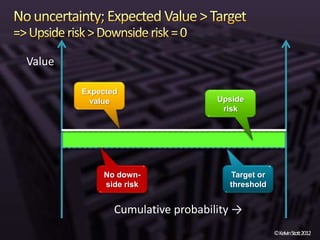
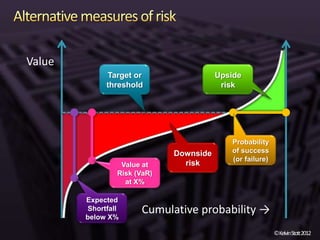
The document discusses the concepts of risk and uncertainty, emphasizing their subjective nature and the difference between them, with risk being associated with potential consequences and uncertainty linked to lack of knowledge. It outlines various types of known and unknown variables, explaining how to measure uncertainty and risk through probability distributions and expected values. Additionally, it describes key metrics such as expected downside/upside risk, value at risk, and expected shortfall, highlighting their importance in assessing potential impacts on targets or thresholds.
More Related Content
Similar to Understanding Risk & Uncertainty
Understanding Risk & Uncertainty
- 1. Kelvin Stott PhD PharmaR&D Portfolio Strategy, Risk & Decision Consultant March 2012 ©KelvinStott2012
- 2. Risk & uncertaintyare closely related, but slightly different concepts Both risk and uncertainty are: Based on current lack of certainty in a potential fact, event, outcome, or scenario, etc. Defined by probabilities or probability distributions Include both upside and downside potential Subjective: they both depend on who knows what Differences Unlike uncertainty, risk involves exposure to impact: potential consequences that matter to a subject Hence, risk is even more subjective: depends on how much the potential consequences matter, to whom Definitions will follow, after more background… ©KelvinStott2012
- 3. Known knowns (norisk/uncertainty) Facts, outcomes or scenarios that we know with absolute certainty, based on deterministic processes Unknown knowns Certain facts that others know but we don’t Based on information asymmetry or poor communication Known unknowns Potential facts, outcomes, scenarios that we are aware of, but don’t yet know with any certainty Based on stochastic processes and known probability laws Unknown unknowns Potential facts, outcomes or scenarios that we are not yet aware of, have not even considered Often rare and extreme events or outliers (“black swans”), not considered due to lack of experience/imagination ©KelvinStott2012
- 4. Discrete Based on uncertainty in discrete variables No intermediate outcomes or scenarios E.g., succeed/fail, true/false, event/no event, etc. Defined by discrete probabilities Continuous Based on uncertainty in continuous variables Intermediate scenarios/outcomes are possible E.g., sales, costs, time, market share, etc. Defined by continuous probability distributions Complex Combination of discrete & continuous uncertainty Most real-life cases fall into this category ©KelvinStott2012
- 5. Discrete Complex Continuous ©KelvinStott2012
- 6. PDF: Probability DensityFunction Probability density vs value Area under curve = CDF (see below) CDF: Cumulative Distribution Function Cumulative probability vs value Gradient = PDF (see above) Area = probability x difference in value Inverted PDF Value vs probability density Inverted CDF Value vs cumulative probability ©KelvinStott2012
- 7. PDF Inverted PDF density Probability Value Invert Probability density Value Integrate / Differentiate Value Inverted CDF Cumulative probability CDF Invert Cumulative probability Value ©KelvinStott2012
- 8. Mean Dispersion Skewness Kurtosis Describes the Describes the Describes the Describes the location of the spread of the asymmetry of shape of the distribution distribution distribution distribution ©KelvinStott2012
- 9. Expected Value (EV)is the probability-weighted average value of a given variable across all potential scenarios Uncertainty is the mean absolute deviation (MAD) from the Expected Value Includes upside and downside uncertainty Upside = downside: they always balance! Risk is the mean absolute deviation (MAD) from a given target, objective, or threshold Includes upside and downside risk Upside risk ≠ downside risk: depends on EV vs target Risk and uncertainty correspond to areas under CDF (or inverted CDF) value-probability curves Areas correspond to Probability x Impact Impact is a deviation (difference) in value ©KelvinStott2012
- 10. Value Upside uncertainty Expected value Downside uncertainty Cumulative probability → ©KelvinStott2012
- 11. Value Upside uncertainty Expected value Downside uncertainty Cumulative probability → ©KelvinStott2012
- 12. Value No upside uncertainty No d’nside Expected uncertainty value Cumulative probability → ©KelvinStott2012
- 13. Value Upside risk Target or threshold Expected value Downside risk Cumulative probability → ©KelvinStott2012
- 14. Value Upside Target or risk threshold Expected value Downside risk Cumulative probability → ©KelvinStott2012
- 15. Value Target or No upside threshold risk No down- Expected side risk value Cumulative probability → ©KelvinStott2012
- 16. Value Target or Upside threshold risk Expected value Downside risk Cumulative probability → ©KelvinStott2012
- 17. Value Target or threshold Upside risk Expected value Downside risk Cumulative probability → ©KelvinStott2012
- 18. Value Target or No upside threshold risk Downside Expected risk value Cumulative probability → ©KelvinStott2012
- 19. Value Upside risk Expected value Downside Target or risk threshold Cumulative probability → ©KelvinStott2012
- 20. Value Upside Expected risk value Downside risk Target or threshold Cumulative probability → ©KelvinStott2012
- 21. Value Expected value Upside risk No down- Target or side risk threshold Cumulative probability → ©KelvinStott2012
- 22. Risk = Uncertaintywhen EV = target/threshold Unlike uncertainty, risk cannot exist without a target, objective, or threshold Risk can exist without uncertainty (but we don’t call it risk), when EV ≠ target/threshold Downside risk always exists when EV < target Upside risk always exists when EV > target Without uncertainty, risk = expected loss/gain If EV = target: upside risk = downside risk = 0 If EV < target: upside risk = 0; downside = target - EV If EV > target: upside risk = EV - target; downside = 0 ©KelvinStott2012
- 23. Standard deviation (SD) Root mean square deviation from Expected Value Measures overall (upside + downside) uncertainty vs EV Non-linear, places more weight on outliers (tails) Variance Mean square deviation from Expected Value Non-linear measure of uncertainty, equal to SD squared Expected downside uncertainty Probability-weighted average negative deviation from EV Linear measure of downside uncertainty only Equal to 0.5 x mean absolute deviation (MAD) vs EV Expected upside uncertainty Probability-weighted average positive deviation from EV Linear measure of upside uncertainty only Equal to 0.5 x mean absolute deviation (MAD) vs EV ©KelvinStott2012
- 24. MAD vs EV/ EV Mean absolute deviation from EV, as % of EV Linear measure of overall (upside + downside) uncertainty vs EV SD / EV Non-linear measure of overall uncertainty, as % of EV Also called the Coefficient of Variation (CV) Variance / EV Non-linear measure of overall uncertainty vs EV; not a % ratio Also called Dispersion Index or Variance-to-Mean Ratio (VMR) Expected downside uncertainty / EV Probability-weighted negative deviation from EV, as % of EV Linear measure of downside UC, equal to 0.5 x MAD vs EV / EV Expected upside uncertainty / EV Probability-weighted positive deviation from EV, as % of EV Linear measure of upside UC, equal to 0.5 x MAD vs EV / EV ©KelvinStott2012
- 25. Value at Risk(VaR) Maximum negative deviation from target/threshold at X% probability Does not consider upside, or potential impact of worst case scenarios Expected Shortfall (ES) Probability-weighted average deviation from target in X% worst cases Measures downside risk across worst case scenarios only Also called Expected Tail Loss (ETL) or Conditional Value at Risk (CVaR) Probability of success or failure to reach target/threshold Commonly used, but does not measure actual risk! Does not consider potential impact of success or failure Expected downside risk Probability-weighted average negative deviation from target/threshold Linear measure of downside risk (probability x negative impact) Expected upside risk Probability-weighted average positive deviation from target/threshold Linear measure of upside risk (probability x positive impact) ©KelvinStott2012
- 26. Value Target or Upside threshold risk Probability Downside of success (or failure) Value at risk Risk (VaR) at X% Expected Shortfall below X% Cumulative probability → ©KelvinStott2012
- 27. MAD vs target/ target Mean absolute deviation from target, as % of target Linear measure of overall risk vs target/threshold VaR / target Value at Risk at X% probability, as % of target Like VaR, does not consider worst case scenarios ES / target Expected Shortfall in X% worst cases, as % of target Linear measure of extreme downside risk vs target Expected downside risk / target Probability-weighted negative deviation, as % of target Expected upside risk / target Probability-weighted positive deviation, as % of target ©KelvinStott2012
- 28. Risk and uncertaintyare based on lack of certainty in a potential fact, event, outcome, or scenario They include both upside & downside components and are described by probability distributions Uncertainty is measured relative to expected value Risk is measured relative to a set target/threshold, with potential consequences that matter (impact) They can be measured in many ways, but the best measures are based on probability-weighted average deviation in value (probability x impact), corresponding to areas under a CDF curve ©KelvinStott2012
- 29. Think and reflect Clicka link to share this presentation Linkedin Google+ Facebook Twitter E-mail Visit or join our Linkedin discussion group Big Ideas in Pharma R&D Productivity & Project / Portfolio Mgt Contact or connect with me kelvin.stott@gmail.com Kelvin Stott on Linkedin ©KelvinStott2012
- 30. kelvin.stott@gmail.com www.linkedin.com/in/kelvinstott ©KelvinStott2012