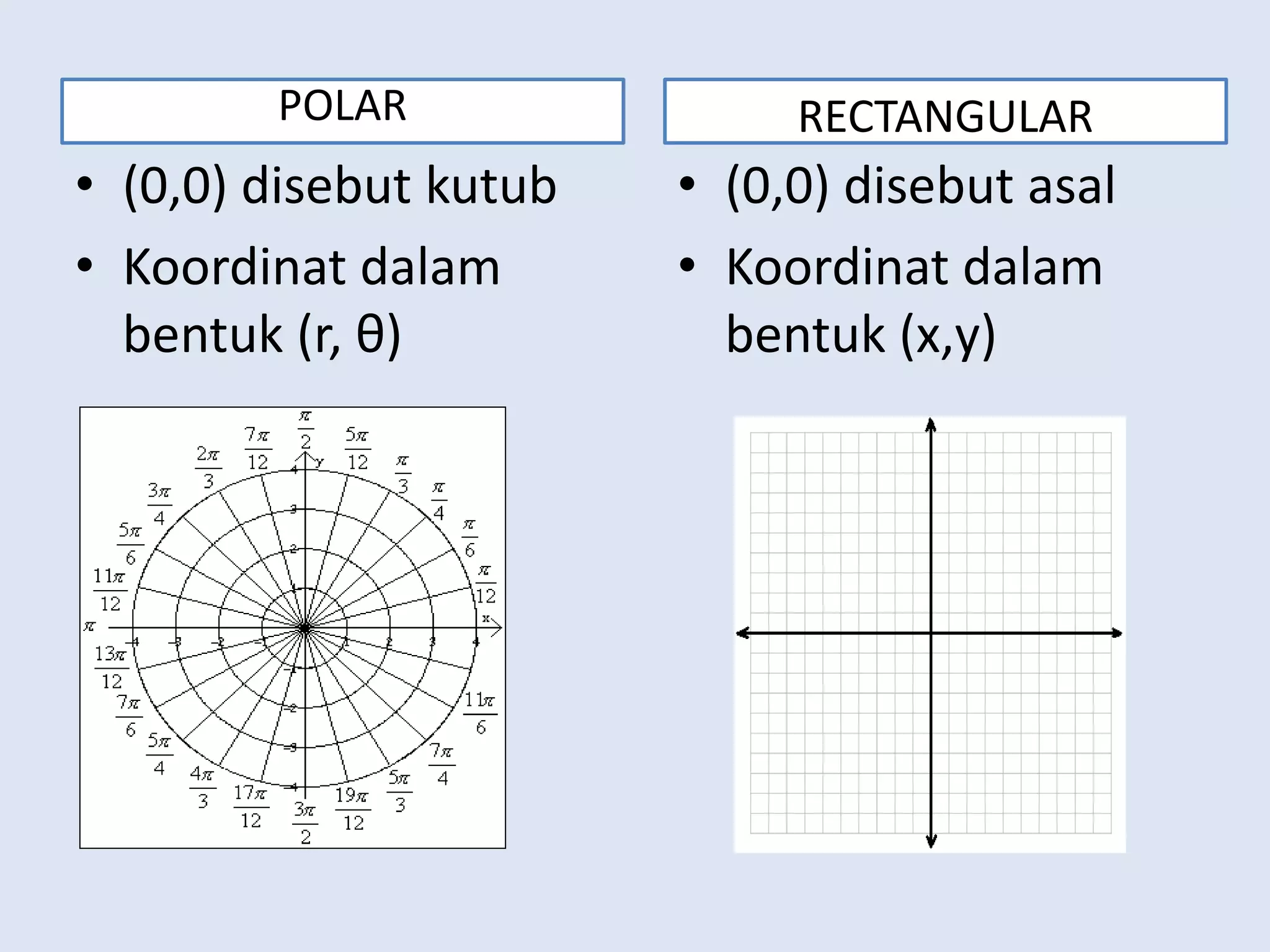
Dokumen tersebut membahas tentang koordinat polar dan konversi antara koordinat polar dan koordinat kartesius. Koordinat polar menggunakan koordinat radial (r) dan sudut (θ) untuk menentukan posisi suatu titik relatif terhadap titik asal dan sumbu polar. Konversi dari koordinat polar ke kartesius menggunakan rumus x = r cosθ dan y = r sinθ, sementara sebaliknya menggunakan rumus r2 = x2 + y2 dan θ = arctan

1. KOORDINAT POLAR
Kelompok 9
Achmad Adhi Nugraha (14512233)
Yasmine Satriani Hapsari (14512234)
Nabila Amalia Putri (14512235)
Kartika Tristanto (14512236)
Rezza Imul Maghfiroh (14512237)
Muh. Agus Parwito (14512238)
Resty Khairun Nissa (14512239)

2. POLAR RECTANGULAR
• (0,0) disebut kutub
• Koordinat dalam
bentuk (r, θ)
• (0,0) disebut asal
• Koordinat dalam
bentuk (x,y)

3. Koordinat polar menunjukkan posisi relatif terhadap titik
kutub O dan sumbu polar (ray) yang diberikan dan berpangkal
pada O.
Titik P dengan koordinat polar (r, ) berarti berada diposisi:
-  derajat dari sumbu-x (sb. polar)
( diukur berlawanan arah jarum-jam)
- berjarak sejauh r dari titik asal kutub O
WARNING!
jika r < 0, maka P berada di posisi yang berlawanan arah.
r: koordinat radial
: koordinat sudut

4. o
(r ,  K1)(r ,  K2)
(r ,  K3) (r ,  K4)
 K1
A
B
C
D
rr
r r
Setiap titik mempunyai lebih dari satu representasi
dalam koordinat polar
(r, ) = (- r,  + n ), untuk n bil. bulat ganjil
= ( r,  + n ) , untuk n bil. bulat genap

5. Konversi Koordinat Polar Kedalam Koordinat Tegak
Gunakan RELASI
x = r cos  , y = r sin 
Maka r2 = x2 + y2,
tan  = y/x, jika x  0
INGAT KEMBALI PRINSIP
KUADRAN
o
(r ,  K1)
(r ,  K2)
(r ,  K3) (r ,  K4)
Jika x >0, maka x berada di kuadran 1 atau 4
jadi -/2 <  < /2   = arctan(y/x).
Jika x < 0, x berada di kuadran 2 atau 3,
 =  + arctan(y/x).
menentukan 

6. Persamaan dalam Koordinat Polar
Persamaan polar dari lingkaran berjari-jari a: r = a
Untuk lingkaran berjari a,
- berpusat di (0,a): r = 2a sin 
- berpusat di (a,0): r = 2a cos 
r 
0 0
2 /2
0 
r 
2 0
0 /2
-2 