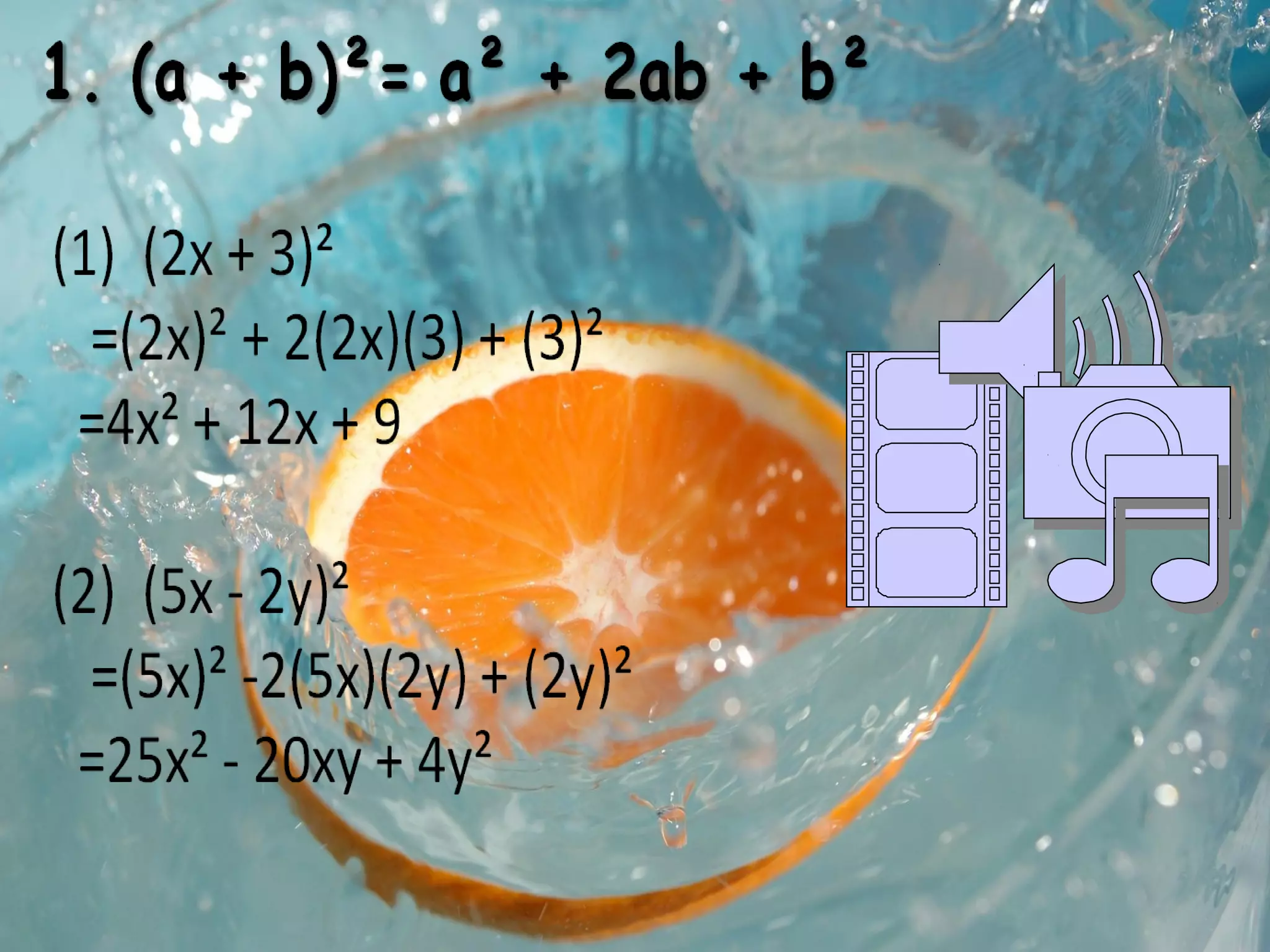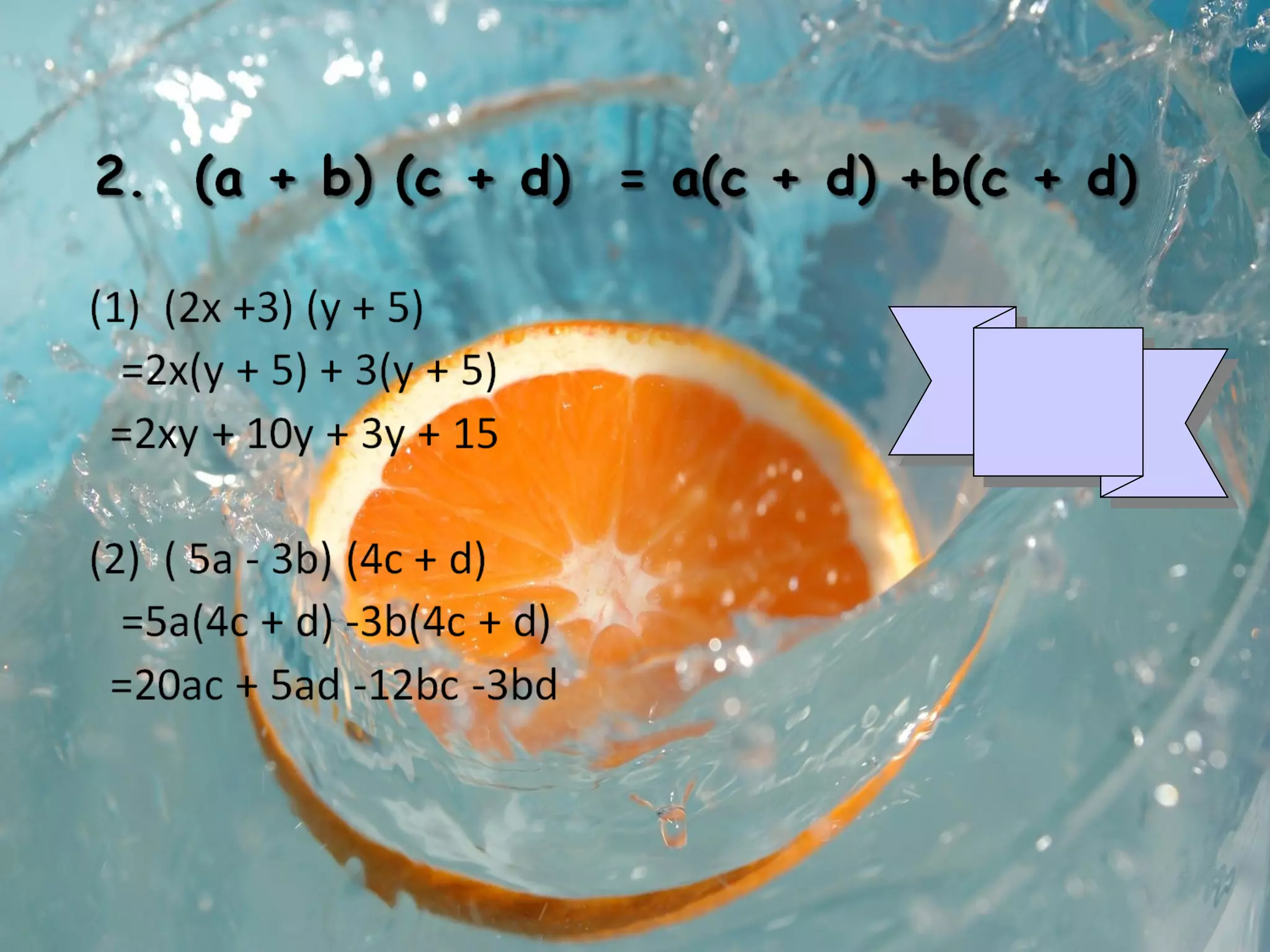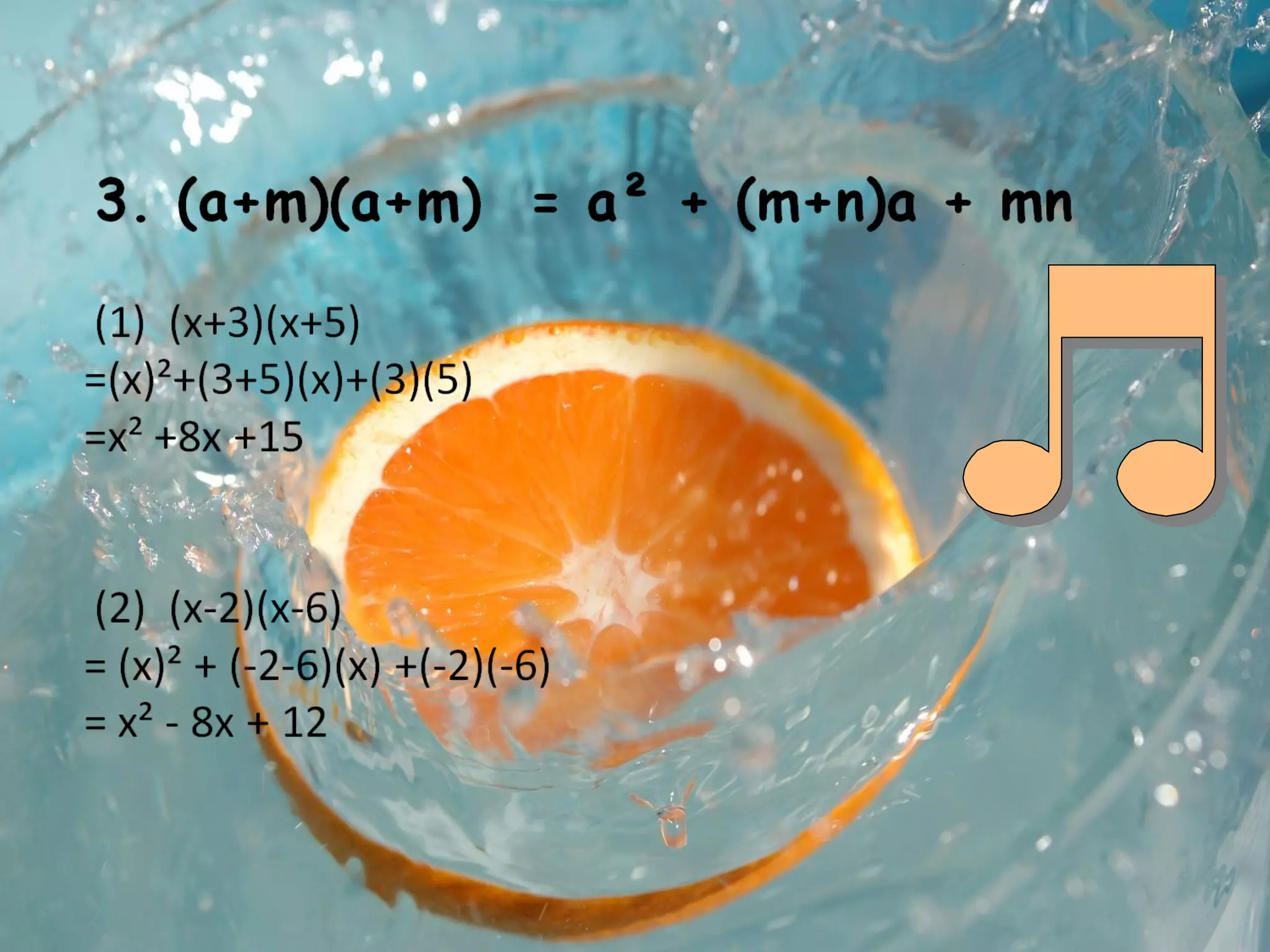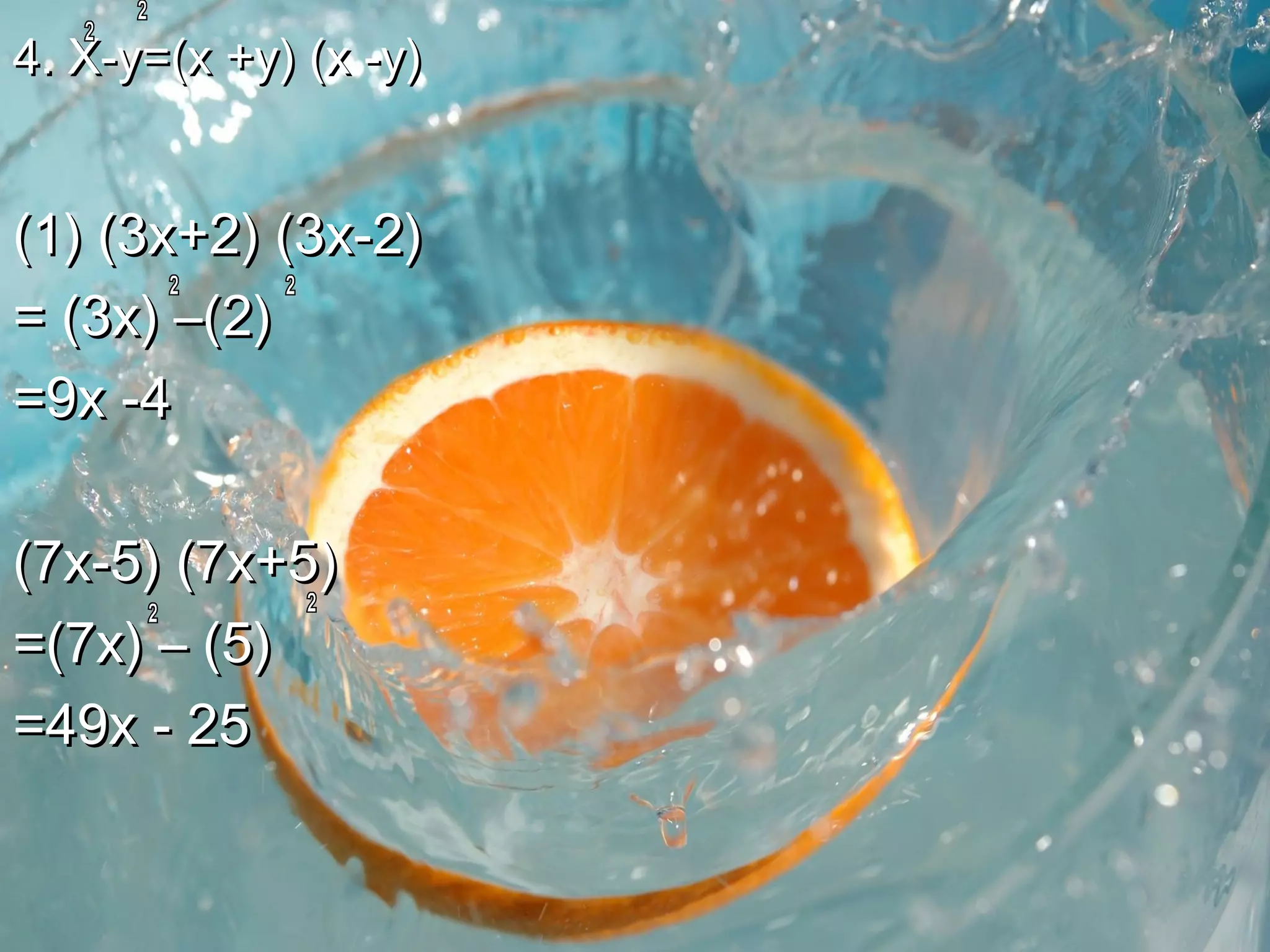This document contains information about polynomials: - A polynomial is an expression with variables and constants using only addition, subtraction, multiplication, and non-negative integer exponents. Each term is a constant multiplied by one or more variables raised to a non-negative integer power. - The degree of a polynomial is equal to the highest exponent in any term. Terms are usually written in descending order of degree. - If two polynomials are equal for all values of the variable, then the coefficients of like powers must be equal, making the polynomials identical.

1. KENDRIYA VIDYALAYA
DHARANGDHRA,
MILATRY AREA
CLASS-9’A
NAME-CH.HARI-NARAYAN.

3. Polynomials
Each term of a polynomial is a product of a
constant (coefficient) and one or more variables
whose exponents are non-negative integers.
e.g. –6a3, 4x3 + x, 3y4 + 2y2 + 1, 6x2y2 – xy + y
-ve
e.g.
4
4a , 5 x ,
x +1
−2

4. Polynomial
• The graph of a polynomial function of degree 3.In
mathematics, a polynomial is an expression of finite
length constructed from variables (also called
indeterminates) and constants, using only the
operations of addition, subtraction, multiplication, and
non-negative integer exponents. However, the division
by a constant is allowed, because the
multiplicative inverse of a non zero constant is also a
constant. For example, x2 − x/4 + 7 is a polynomial,
but by the variable x (4/x), and also because its third
term contains an exponent that is not an integer (3/2).
The term "polynomial" can also be used as an
adjective, for quantities that can be expressed as a
polynomial of some parameter, as in polynomial time,
which is used in computational complexity theory

5. 3.1 Review on Polynomials
(A) Monomials and Polynomials
A monomial is a an algebraic
expression containing one term, which
may be a constant, a positive integral
power of a variable or a product of
powers of variables.
e.g. 4, 2x3 and 3x2y

6. quotient
− x − 2x + 1
4
3
2
− x + 0 x + 4 x − 3x + 1
divisor
dividend
− x + 2x − x
4
3
2
2
− 2 x + 5 x − 3x
3
2
− 2x + 4x − 2x
3
2
x −x +
1
2
x 2 −2 x +
1
remainder
x

7. The degree of a polynomial is equal to the
highest degree of its terms.
The terms of a polynomials are usually
written in descending order (i.e. the
terms are arranged in descending
degree).

8. Equality of Polynomials
If two polynomials in x are equal for
all values of x, then the two
polynomials are identical, and the
coefficients of like powers of x in
the two polynomials must be equal.

9. Alternative Method
When x = 2,
3(2)2 - 5(2) - 5 = [A+3(2)](2-2) + B
12-10-5 = B
B = -3
When x = 0,
3(0)2 - 5(0) – 5 = [A+3(0)](0-2) + B
-5 = -2A + B
-5 = -2A – 3
-2 = -2A
A=1

10. (B) Remainder Theorem
9
3 28
27
28 = 3 x 9 + 1
dividend
divisor
remainder
quotient
1

11. Applications of Theorems about
Polynomials
(A)Use Factor Theorem to factorize a
polynomial of degree 3 or above
(1) try to put a = +1, -1, +2, -2, +3, -3, …. one by one into
the polynomial until the function is equal to zero.
(2) as the function is equal to zero, then (x – a) is one of the
factors.
(3) divide the polynomial by (x – a) to get the quotient which
is the other factor of the polynomial.
(4) factorize the quotient by the method you have learnt in
before.

16. 4. X-y=(x +y) (x -y)
(1) (3x+2) (3x-2)
= (3x) –(2)
=9x -4
(7x-5) (7x+5)
=(7x) – (5)
=49x - 25

29. Maths Presentation Ppt