This document discusses key concepts related to investing, including:
- The differences between saving (short-term goals) and investing (long-term goals)
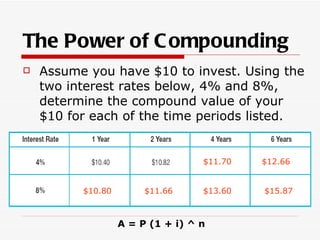
- The impact of time on the value of money through compound interest and inflation
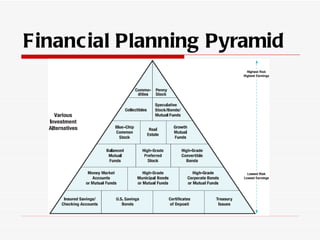
- Common investment options like stocks, bonds, and mutual funds that provide different balances of risk and reward
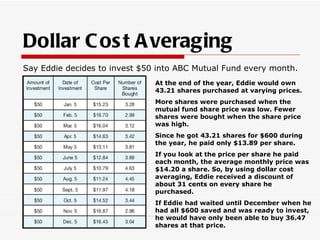
- Strategies for successful investing like diversification and dollar cost averaging to reduce risk over time