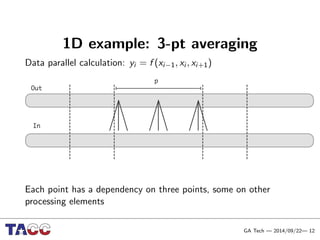
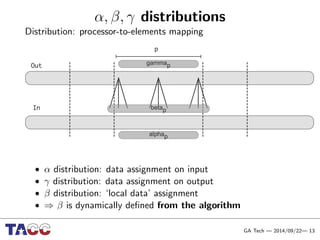
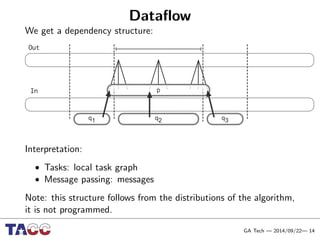
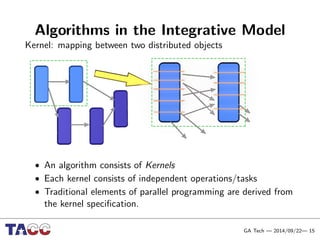
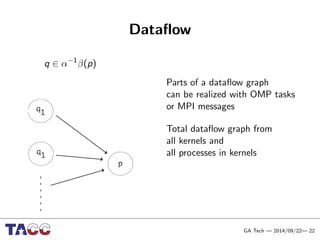
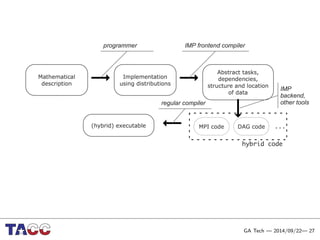
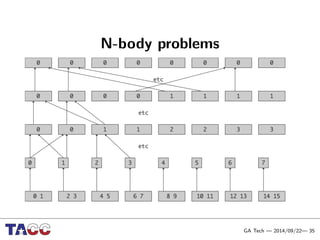
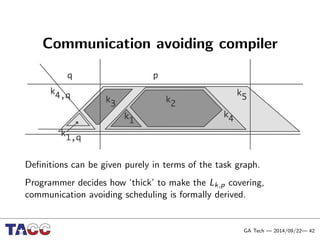
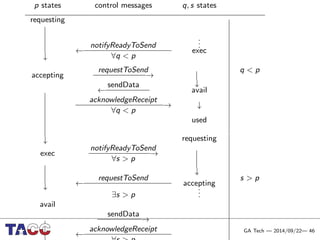
This document presents an Integrative Model for Parallelism (IMP) that aims to provide a unified treatment of different types of parallelism. It describes the key concepts of the IMP including the programming model using sequential semantics, the execution model using a data flow virtual machine, and the data model using distributions to describe data placement. It demonstrates the IMP concepts using a motivating example of 3-point averaging and discusses tasks, processes, and research opportunities around the IMP approach.

1. Integrative Parallel Programming in HPC
Victor Eijkhout
2014/09/22

2. Introduction
Motivating example
Type system
Demonstration
Other applications
Tasks and processes
Task execution
Research
Conclusion
GA Tech | 2014/09/22| 2

3. Introduction
GA Tech | 2014/09/22| 3

4. My aims for a new parallel programming
system
1. There are many types of parallelism
) Uniform treatment of parallelism
2. Data movement is more important than computation
) While acknowledging the realities of hardware
3. CS theory seems to ignore HPC-type of parallelism
) Strongly theory based
IMP: Integrative Model for Parallelism
GA Tech | 2014/09/22| 4

5. Design of a programming system
One needs to distinguish:
Programming model How does it look in code
Execution model How is it actually executed
Data model How is data placed and moved about
Three dierent vocabularies!
GA Tech | 2014/09/22| 5

6. Programming model
Sequential semantics
[A]n HPF program may be understood (and debugged)
using sequential semantics, a deterministic world that we are
comfortable with. Once again, as in traditional programming,
the programmer works with a single address space, treating an
array as a single, monolithic object, regardless of how it may
be distributed across the memories of a parallel machine.
(Nikhil 1993)
As opposed to
[H]umans are quickly overwhelmed by concurrency and

7. nd it much more dicult to reason about concurrent than
sequential code. Even careful people miss possible interleavings
among even simple collections of partially ordered operations.
(Sutter and Larus 2005)
GA Tech | 2014/09/22| 6

8. Programming model
Sequential semantics is close to the mathematics of the problem.
Note: sequential semantics in the programming model does not
mean BSP synchronization in the execution.
Also note: sequential semantics is subtly dierent from SPMD
(but at least SPMD puts you in the asynchronous mindset)
GA Tech | 2014/09/22| 7

9. Execution model
Virtual machine: data
ow.
Data
ow expresses the essential dependencies in an
algorithm.
Data
ow applies to multiple parallelism models.
But it would be a mistake to program data
ow explicitly.
GA Tech | 2014/09/22| 8

10. Data model
Distribution: mapping from processors to data.
(note: traditionally the other way around)
Needed (and missing from existing systems such as UPC, HPF):
distributions need to be

11. rst-class objects:
) we want an algebra of distributions
algorithms need to be expressed in distributions
GA Tech | 2014/09/22| 9

12. Integrative Model for Parallelism (IMP)
Theoretical model for describing parallelism
Library (or maybe language) for describing operations on
parallel data
Minimal, yet sucient, speci

13. cation of parallel aspects
Many aspects are formally derived (often as

14. rst-class
objects), including messages and task dependencies.
) Specify what, not how
) Improve programmer productivity, code quality, eciency
and robustness
GA Tech | 2014/09/22| 10

15. Motivating example
GA Tech | 2014/09/22| 11

16. 1D example: 3-pt averaging
Data parallel calculation: yi = f (xi1; xi ; xi+1)
Each point has a dependency on three points, some on other
processing elements
GA Tech | 2014/09/22| 12

17. ;

18. ;
distributions
Distribution: processor-to-elements mapping
distribution: data assignment on input
distribution: data assignment on output

19. distribution: `local data' assignment
)

20. is dynamically de

21. ned from the algorithm
GA Tech | 2014/09/22| 13

22. Data
ow
We get a dependency structure:
Interpretation:
Tasks: local task graph
Message passing: messages
Note: this structure follows from the distributions of the algorithm,
it is not programmed.
GA Tech | 2014/09/22| 14

23. Algorithms in the Integrative Model
Kernel: mapping between two distributed objects
An algorithm consists of Kernels
Each kernel consists of independent operations/tasks
Traditional elements of parallel programming are derived from
the kernel speci

24. cation.
GA Tech | 2014/09/22| 15

25. Type system
GA Tech | 2014/09/22| 16

26. Generalized data parallelism
Functions
f : Realk ! Real
applied to arrays y = f (x):
yi = f
x(If (i))
This de

27. nes function
If : N ! 2N
for instance If = fi ; i 1; i + 1g.
GA Tech | 2014/09/22| 17

28. Distributions
Distribution is (non-disjoint, non-unique) mapping from processors
to sets of indices:
d : P ! 2N
Distributed data:
x(d) : p7! fxi : i 2 d(p)g
Operations on distributions:
g : N ! N ) g(d) : p7! fg(i) : i 2 d(p)g
GA Tech | 2014/09/22| 18

29. Algorithms in terms of distributions
If d is a distribution, and (funky notation)
x y x + y; x y x y
the motivating example becomes:
y(d) = x(d) + x(d 1) + x(d 1)
and the

30. distribution is

31. = d [ d 1 [ d 1
To reiterate: the

32. distribution comes from the structure of the
algorithm
GA Tech | 2014/09/22| 19

33. Transformations of distributions
How do you go from the to

34. distribution of a distributed object?
x(

35. ) = T(;

36. )x() whereT(;

37. ) = 1

38. De

39. ne 1

40. : P ! 2P by:
q 2 1

41. (p) (q)

42. (p)6= ;
`If q 2 1

43. (p), the task on q has data for the task on p'
OpenMP: task wait
MPI: message between q and p
GA Tech | 2014/09/22| 20

44. Parallel computing with transformations
Let y(
) distributed output, then (total needed input)

45. = If (
)
so
y(
) = f
x(

46. )
;

47. = If (
)
is local operation. However, x(), so
y = f (Tx)
8
:
y is distributed as y(
)
x is distributed as x()

48. = If
T = 1

49. GA Tech | 2014/09/22| 21

50. Data
ow
q 2 1

51. (p)
Parts of a data
ow graph
can be realized with OMP tasks
or MPI messages
Total data
ow graph from
all kernels and
all processes in kernels
GA Tech | 2014/09/22| 22