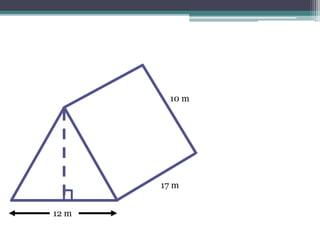
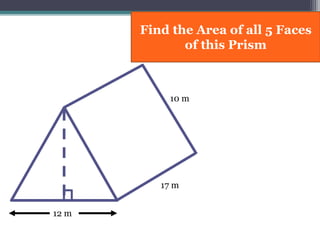
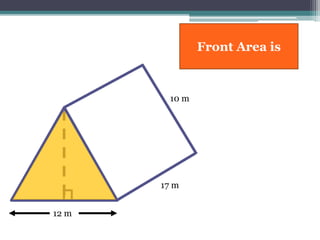
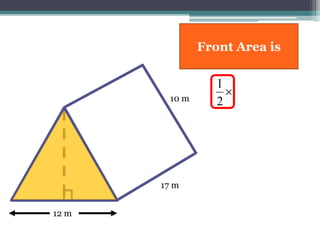
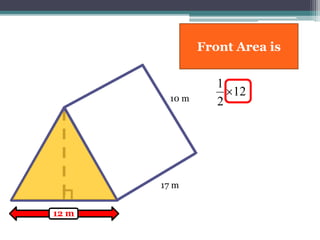
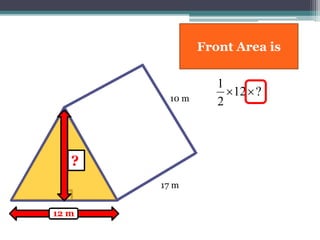
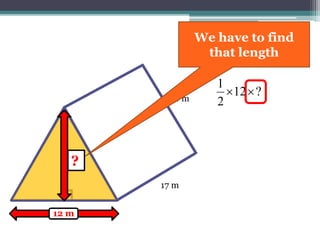
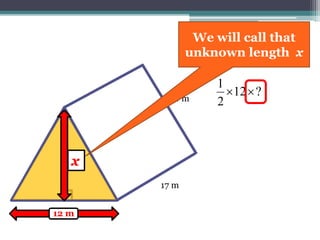
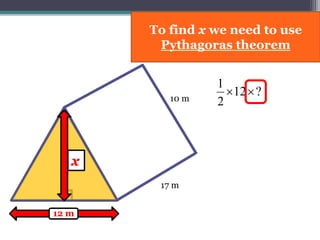
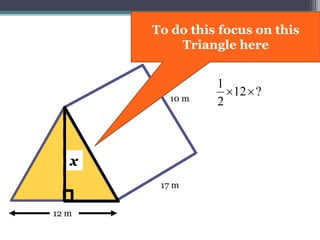
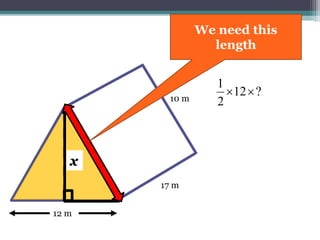
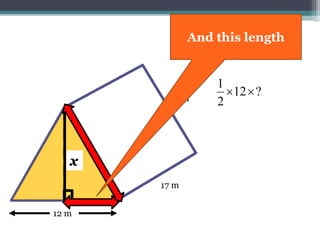
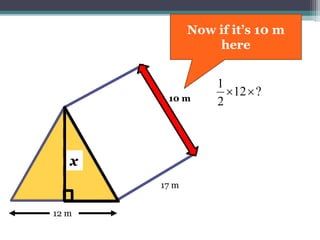
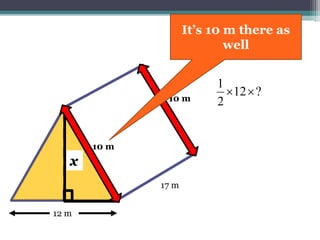
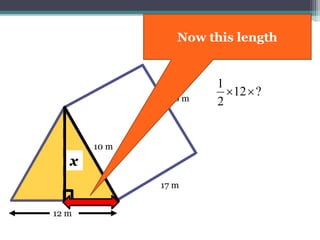
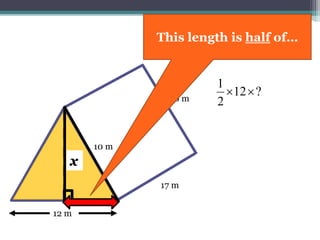
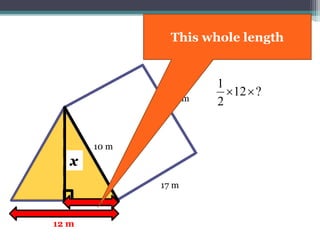
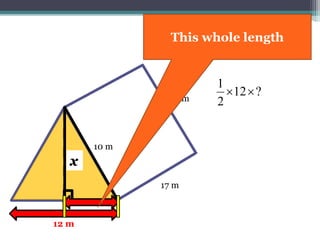
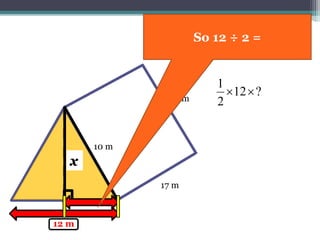
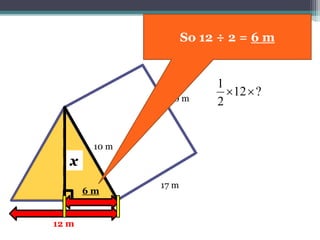
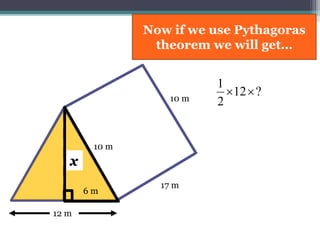
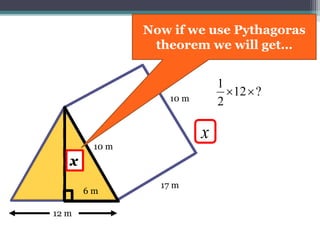
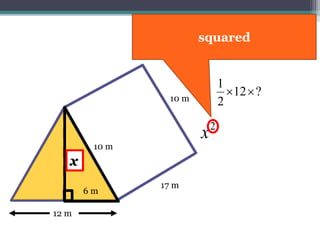
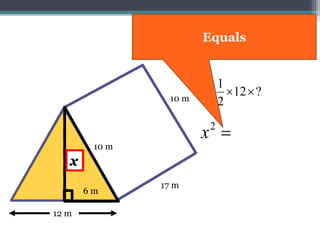
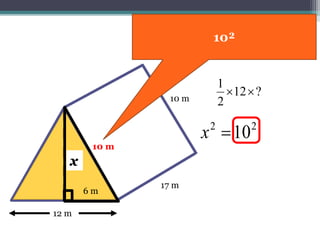
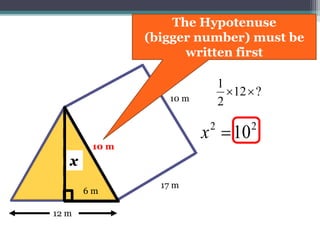
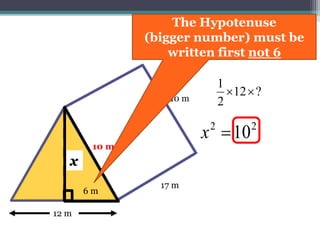
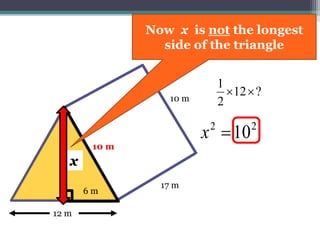
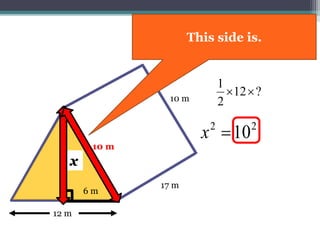
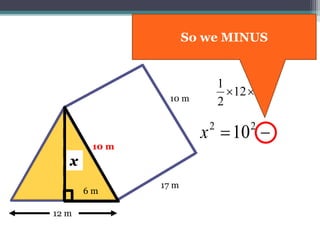
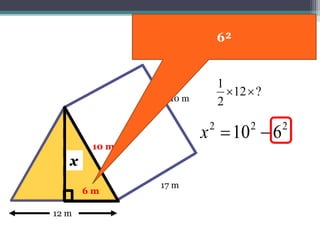
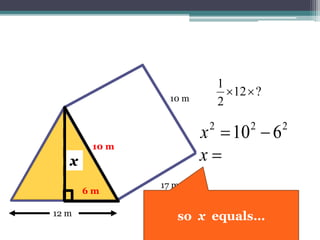
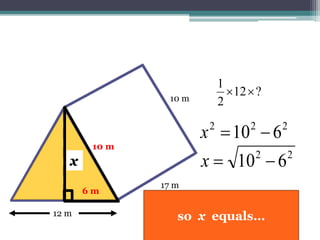
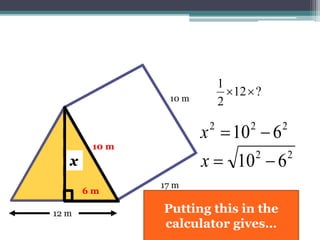
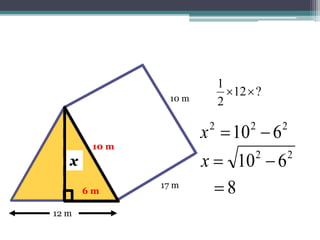
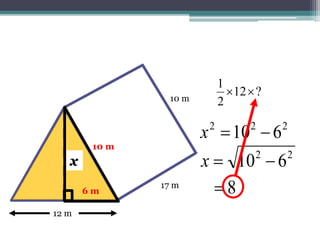
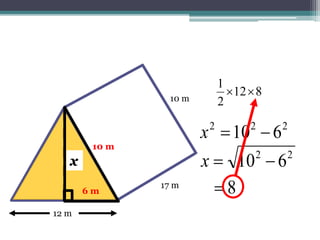
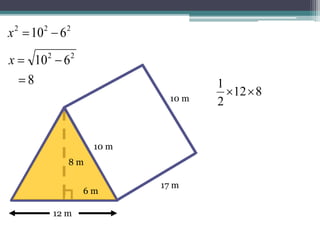
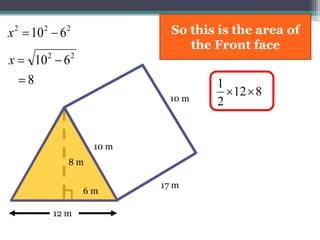
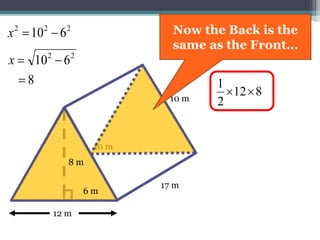
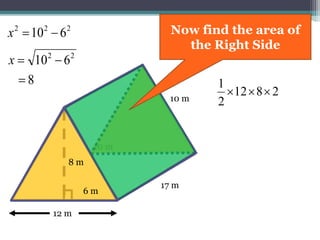
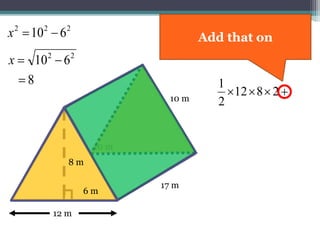
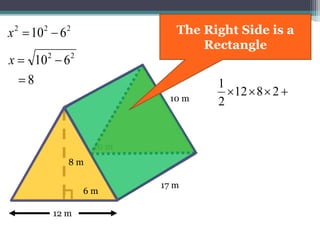
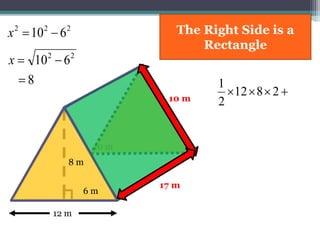
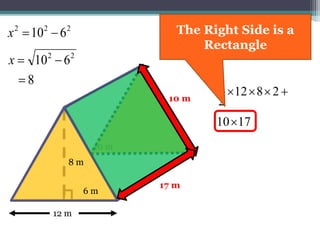
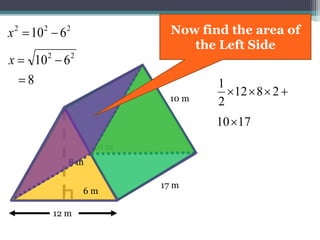
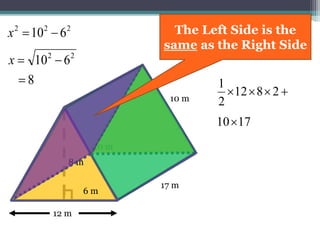
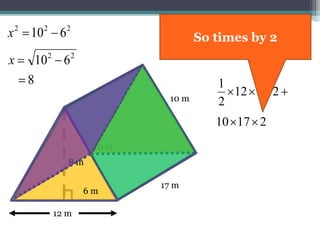
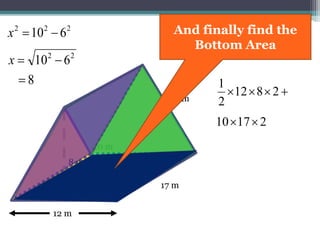
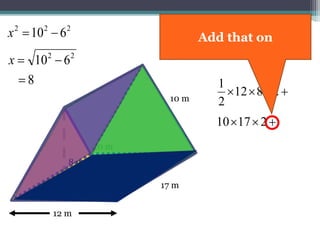
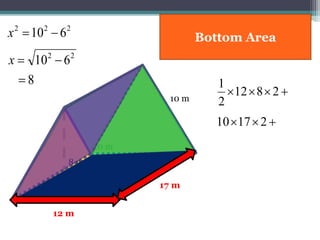
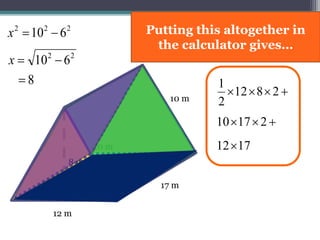
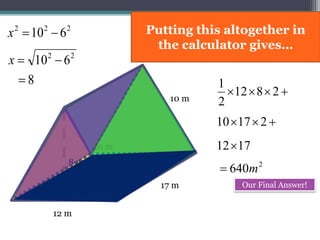
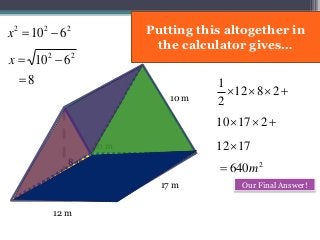
This document focuses on calculating the surface area of a triangular prism with dimensions of 10m, 12m, and 17m. It details the steps involved, including the use of the Pythagorean theorem to find unknown lengths and the calculation of areas for each face of the prism. The final surface area calculated amounts to 2640 m².

1. Finding: Surface Area of
Triangular Prism 3
- Mr Kim

2. Please view:
Surface Area of Triangular Prism 1 & 2
Before you view this lesson

3. 10 m
12 m
17 m

4. 10 m
12 m
Find the Area of all 5 Faces
of this Prism
17 m

5. 17 m
10 m
12 m
Front Area is

6. 17 m
10 m
12 m
Front Area is

2
1

7. 17 m
10 m
12 m
Front Area is
12
2
1


8. 17 m
10 m
Front Area is
?12
2
1

?
12 m

9. 17 m
10 m
?12
2
1

?
We have to find
that length
12 m

10. 17 m
10 m
?12
2
1

We will call that
unknown length x
x
12 m

11. 17 m
10 m
?12
2
1

To find x we need to use
Pythagoras theorem
x
12 m

12. 17 m
10 m
12 m
?12
2
1

x

13. 17 m
10 m
12 m
?12
2
1

x
Focus on this Triangle here

14. 17 m
10 m
12 m
?12
2
1

x
We need this
length

15. 17 m
10 m
12 m
?12
2
1

x
And this length

16. 17 m
10 m
12 m
?12
2
1

x
Now if it’s 10 m
here

17. 17 m
10 m
12 m
?12
2
1

x
10 m
It’s 10 m there as
well

18. 17 m
10 m
12 m
?12
2
1

x
10 m
Now this length

19. 17 m
10 m
12 m
?12
2
1

x
10 m
This length is half of…

20. 17 m
10 m
12 m
?12
2
1

x
10 m
12 m
This whole length

21. 17 m
10 m
12 m
?12
2
1

x
10 m
12 m
This whole length

22. 17 m
10 m
12 m
?12
2
1

x
10 m
12 m
So 12 ÷ 2 =

23. 17 m
10 m
12 m
?12
2
1

x
10 m
12 m
So 12 ÷ 2 = 6 m
6 m

24. 17 m
10 m
12 m
?12
2
1

x
10 m
6 m
Now if we use Pythagoras
theorem we will get…

25. 17 m
10 m
12 m
?12
2
1

x
10 m
6 m
x
x
Now if we use Pythagoras
theorem we will get…

26. 17 m
10 m
12 m
?12
2
1

x
10 m
6 m
x
2
x
squared

27. 17 m
10 m
12 m
?12
2
1

x
10 m
6 m
x
2
x
Equals

28. 17 m
10 m
12 m
?12
2
1

x
6 m
x
10 m
22
10x
10²

29. 17 m
10 m
12 m
?12
2
1

x
6 m
x
10 m
22
10x
The Hypotenuse
(10 m) must be written first

30. 17 m
10 m
12 m
?12
2
1

x
6 m
x
10 m
22
10x
The Hypotenuse
(10 m) must be written first
not 6

31. 17 m
10 m
12 m
?12
2
1

x
6 m
x
10 m
22
10x
10 m
Now x is not the longest
side of the triangle

32. 17 m
10 m
12 m
?12
2
1

x
6 m
x
10 m
22
10x
10 m
This side is.

33. 17 m
10 m
12 m
?12
2
1

x
6 m
x
10 m10 m
 22
10x
So we MINUS

34. 17 m
10 m
12 m
?12
2
1

xx
10 m10 m
6 m
6²
222
610 x

35. 17 m
10 m
12 m
?12
2
1

xx
10 m10 m
6 m
222
610 x
so x equals…
x

36. 17 m
10 m
12 m
?12
2
1

xx
10 m10 m
6 m
222
610 x
so x equals…
22
610 x

37. 17 m
10 m
12 m
?12
2
1

xx
10 m10 m
6 m
222
610 x
22
610 x
Putting this in the
calculator gives…

38. 17 m
10 m
12 m
?12
2
1

xx
10 m10 m
6 m
222
610 x
22
610 x
8

39. 17 m
10 m
12 m
?12
2
1

xx
10 m10 m
6 m
222
610 x
22
610 x
8

40. 17 m
10 m
12 m
xx
10 m10 m
6 m
222
610 x
22
610 x
8
812
2
1


41. 17 m
10 m
812
2
1

10 m
6 m
12 m
22
610 x
222
610 x
8
8 m

42. 17 m
10 m
812
2
1

10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
So this is the area of
the Front face

43. 17 m
10 m
812
2
1

10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
Now the Back is the
same as the Front…

44. 17 m
10 m
2812
2
1

10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
So times by 2

45. 17 m
10 m
2812
2
1

10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
Now find the area of
the Right Side

46. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
Add that on

47. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
The Right Side is a
Rectangle

48. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
The Right Side is a
Rectangle

49. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
The Right Side is a
Rectangle
1710

50. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
1710
Now find the area of
the Left Side

51. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
1710
The Left Side is the
same as the Right Side

52. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
21710 
So times by 2

53. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
21710 
And finally find the
Bottom Area

54. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
 21710
Add that on

55. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
 21710
Bottom Area

56. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
 21710
Bottom Area
1712

57. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
 21710
1712
Putting this altogether in
the calculator gives…

58. 17 m
10 m
 2812
2
1
10 m
6 m
12 m
22
610 x
222
610 x
8
8 m
 21710
1712
2
640m
Our Final Answer!
Putting this altogether in
the calculator gives…