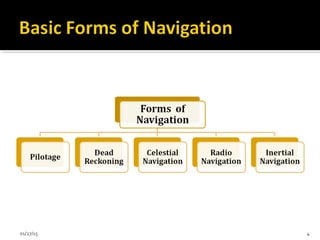
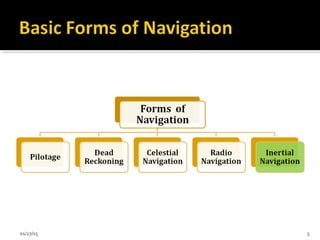
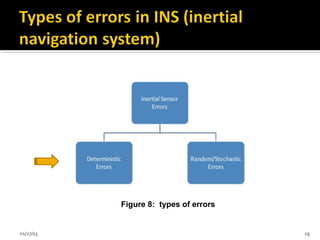
This document discusses inertial navigation sensor calibration. It provides an introduction to inertial navigation sensors and methods for calibrating accelerometers and gyroscopes. It describes the components of an inertial measurement unit and common calibration methods like the six position static test. Applications of inertial sensors in areas like navigation, tracking, and robotics are also mentioned.

1. By: Vikas Kumar Sinha
Control Systems (M.Tech)
01/27/15 1
Inertial Navigation Sensor Calibration

2.  Introduction
 Inertial Navigation sensor
 Accelerometer
 Gyroscope
 Methods of calibration
 Applications
 Conclusion
 References
01/27/15 2

3. Navigation is a field of study that
focuses on the process of monitoring
and controlling the movement of a
craft or vehicle from one place to
another.
01/27/15 3

4. 01/27/15 4

5. 01/27/15 5

6.  Inertial navigation is a self-contained
navigation technique.
 In which measurements provided by
accelerometers and gyroscopes.
 To track the position and orientation of an
object relative to a known starting point.
01/27/15 6

7. Figure 1: The body and global frames of reference[10].
01/27/15 7

8.  An inertial measurement unit (IMU)
measures linear and angular motion in
three dimensions without external
reference.
 The IMU consists of two orthogonal
sensor triads, one consisting of three
accelerometers, the other of three
gyroscopes
01/27/15 8

9. Figure 2: Inertial measurement unit [12].
01/27/15 9

10. • If we can measure the acceleration of a vehicle we can
• integrate the acceleration to get velocity
• integrate the velocity to get position
• Then, assuming that we know the initial position and
velocity we can determine the position of the vehicle at
ant time t.
Formula: ..(1)
01/27/15 10

11. Figure 3: Aircraft Axes
01/27/15 11

12. The three axes of the aircraft are:
The roll axis which is roughly parallel to the line joining the nose
and the tail
Positive angle: right wing down
The pitch axis which is roughly parallel to the line joining the
wingtips
Positive angle: nose up
The yaw axis is vertical
Positive angle: nose to the right
01/27/15 12

13.  Accelerometers are defined as acceleration
sensors that measure the non-gravitational
linear acceleration along their sensitive
axis.
 F=m*a …(2)
 F=k*x …(3)
Where:
F= force
m= mass
a=acceleration
x= displacement
01/27/15 13

14.  In this way
X α A ………(4)
Figure 4: basic sturcture of accelerometer [8]
01/27/15 14

15. Figure: 5
01/27/15 15

16.  A gyroscope is a device for measuring of
maintaining orientation based on the
principle of angular momentum(rotation
momentum)
Figure 6: Gyroscope
01/27/15 16

17.  Uses Coriolis effect using vibrating elements
▪ Fc -Force m -mass w -angular velocity v –velocity
Figure 7: Coriolis effect [10]
01/27/15 17

18. 01/27/15 18

19. Figure 8: types of errors
01/27/15 19

20. Figure 9: Relationship between the output voltage of the
accelerometer(gyro) and the measured force(angular rate) [10].
01/27/15 20

21. ….(5)
….(6)
Where:
a = true specific force vector
ω = body frame rotation rate vector
b = bias vector
S = scale factor matrix
N = non-orthogonality error matrix
η = non-deterministic accelerometer errors
01/27/15 21

22.  Six Position Static Test
 Improved Six Position Static Test
 Multi-Position Calibration Method
01/27/15 22

23. …(7)
…(8)
…(9)
..(10)
01/27/15 23
Where,
= sensor measurement when sensitive axis is pointed upward.
= sensor measurement when the sensitive axis is pointed
downwards

24. ….(11)
 the ideal accelerations would be measured
as:
…(12)01/27/15 24

25. The raw output of the sensors (in volts)
constitutes the matrix Y:
…(13)
01/27/15 25

26.  Using the least squares method as follows:
…(14)
01/27/15 26

27. 01/27/15 27

28. Figure 10: Misalignment to n-frame [23].
01/27/15 28

29. General calibration model as below for accelerometer :
…(17)
By using the same methodology, we can derive the general model for the
gyros as:
…(18)
Where ωe is the true Earth rotation rate.
01/27/15 29

30. Rotation matrix:
, Ry
…(19)
The non-orthogonality of the z axis can be expressed by two consecutive rotations;
rotation about the x axis by θzx and about the y axis by θzy.
…(20)
01/27/15 30

31. ...
(21)
 The accelerometers on the IMU axes sense the following values:
. .. ..(22)
01/27/15 31

32.  Inclusion of the major errors, bias and
scale factor error, into the IMU data is
done by the equation below:
..(23)
 Where Ya , b, a ,s IMU observation, bias
and scale factor error, respectively, for the
accelerometer and i = x, y and z.
01/27/15 32

33.  The observation equations for the accelerometer sensors
on the IMU axis triad will be obtained as below:
...(24)
01/27/15 33

34.  The true values for the specific force
vector components are found as:
(25)
01/27/15 34

35. 01/27/15 35
calibration models for gyroscope and accelerometer errors:
…(26)

36.  The XSENS 300 MTi-G is an integrated GPS
and Inertial Measurement Unit (IMU).
 Small size,
 Weight,
 Low cost and low complexity in use
 wide range of interface options
 XSENS 300 MTi-G gives output if it is
rotated in three dimension space.
01/27/15 36

37. 01/27/15
Figure 11: XSENS 300 MTi-G.
37

38. 01/27/15 38
Figure 12 : MT Manager showing a 3D view of an MTi-G-700 GPS/INS.

39. 01/27/15 39
Figure 13: MT Manager showing inertial data of an MTi-G-700 GPS/INS.

40.  Navigation
 Use in quadcopter
 Tracking
 Robotics
 Aircraft
01/27/15 40

41.  We estimate the value of bias, scale and
non-orthogonality errors.
 By using these methods we will get an error
less IMU sensor.
01/27/15 41

42.  To calibrate the INS by optimization
 To evaluate the contribution of the
calibration and stochastic error modeling
with thermal compensation
 Investigation of a general model including
both deterministic and stochastic noise
terms
01/27/15 42

43.  [1] M. Li, A.I. Mourikis, ''3-D Motion Estimation and Online Temporal Calibration for
Camera-IMU Systems,'' Proceedings of the IEEE International Conference on Robotics
and Automation (ICRA), Karlsruhe, Germany, May 2013.
 [2] M. Li, B. Kim, A.I. Mourikis, ''Real-time Motion Tracking on a Cellphone using Inertial
Sensing and a Rolling Shutter Camera,'' Proceedings of the IEEE International Conference
on Robotics and Automation (ICRA), Karlsruhe, Germany, May 2013.
 [3] M. Li, A.I. Mourikis, ''Optimization-Based Estimator Design for Vision-Aided Inertial
Navigation,'' Proceedings of the Robotics: Science and Systems Conference (RSS),
Sydney, Australia, July 2012.
 [4] M. Li, A.I. Mourikis, ''High-Precision, Consistent EKF-based Visual-Inertial Odometry,''
International Journal of Robotics Research (IJRR), Volume 32, No 6, May 2013.
 [5] M. Li, A.I. Mourikis, ''Vision-aided Inertial Navigation with Rolling-Shutter Cameras,''
International Journal of Robotics Research (IJRR).
01/27/15 43

44.  [6] S. Thomas, The Last Navigator: "A Young Man, An Ancient Mariner, the Secrets of the
Sea", McGraw-Hill, New York, 1997.
 [7] Adem G. Hayal, "Static Calibration of Tactical Grade Inertial Measurement Units",
Geodetic Science Report No. 496, The Ohio State University Columbus, Ohio 43210, Sep
2008.
 [8] Priyanka Aggarwal, Zainab Syed, Aboelmagd Noureldin, Naser El-Sheimy, "MEMS
Based Integrated Navigation", GNSS Technology and Application Series, ISBN-13:
978-1-60807-043-5, 2010.
 [9] Hofmann-Wellenhof, B., Lichtenegger, H., and Collins, J., "GPS Theory and Practice",
Fifth Edition, Austria: Springer, 2004.
 [10] Grewal, M.S., Weill, L., and Andrews, A.P., "Global Positioning Systems, Inertial
Navigation, and Integration", Second Edition, New Jersey: John Wiley & Sons, 2007.
01/27/15 44

45.  [11] CLAUDIA C. MERUANE NARANJO, "Analysis and Modeling of MEMS based
Inertial Sensors", Signal Processing, School of Electrical Engineering, XR-EE-SB
2008:011, Stockholm 2008.
 [12] Lotters J C, Schipper J, Veltink P H, Olthuis W and Bergveld P, "Procedure for in-use
calibration of triaxial accelerometers in medical application", Sensors Actuators
A68221–8, 1998.
 [13] N. El-Sheimy, S. Nassar and A. Noureldin, "Wavelet De-Noising for IMUAlignment",
IEEE Aerospace and Electronics Systems Magazine, vol. 19, pp. 32- 39, Oct. 2004.
 [14] Aggarwal, P., et al., "A Standard Testing and Calibration Procedure for Low Cost
MEMS Inertial Sensors and Units", Journal of Navigation, Vol. 61, No. 2, 2007, pp. 323–
336.
 [15] Hou, H., and El-Sheimy, N., "Inertial Sensors Errors Modeling Using Allan Variance,"
Proceedings of ION GNSS 2003, Portland, Oregon, Sept. 9–12, 2003.
 [16] Hide, C.D., Integration of GPS and Low Cost INS Measurements, Ph.D. thesis, Institute
of Engineering, Surveying and Space Geodesy, University of Nottingham, U.K., 2003.
01/27/15 45

46.  [17] CLAUDIA C. MERUANE NARANJO, "Analysis and Modeling of MEMS based
Inertial Sensors", Signal Processing, School of Electrical Engineering, XR-EE-SB
2008:011, Stockholm 2008.
 [18] El-Sheimy N, " Inertial Techniques and INS/DGPS Integration", Dept. of Geomatics
Enggineering., University of Calgary, Calgary, Canada, 2003.
 [19] Ren Wei Zhang Tao, Zhang Hai-yun, Wang Lei-gang, Zhaou Yong-jie, Luan
Mengkai, Liu Hui-feng, Shi Jing-wei,"A Research on Calibration of Low-Precision MEMS
Inertial Sensors", 25th Chinese Control and Decision Conference (CCDC), 2013.
 [20] P. Aggarwal, Z. Syed, X. Niu, and N. El-Sheimy, "A standard testing and calibration
procedure for low cost MEMS inertial sensors and units," Journal of navigation, vol. 61, pp.
323-336, 2008.
 [21] Titterton, D. H. and Weston, J. L. (1997). "Strapdown Inertial Navigation
Technology". Peter Peregrinus Ltd, UK.
01/27/15 46

47.  [22] Niu X, “Micromachined Attitude Measurement Unit with Application in Satellite TV Antenna
Stabilization”, PhD Dissertation, Department of Precision Instruments and Machinery, Tsinghua
University, 2002.
 [23] Shin E-H and El-Sheimy N, "A New calibration Method for Strapdown Inertial Navigation
Systems", Z. Vermess, 127 1-10, 2002.
 [24] Lawrence C. Ng and DarryII J. Pines. (1997), "Characterization of Ring Laser Gyro
Performance Using the Allan Variance Method" , Journal of Guidance, Control, and Dynamics, Vol.
20, No. 1: Engineering Notes, p 211 -214. January - February, 1997.
 [25] IEEE Std 952, "IEEE Standard Specification Format Guide and Test Procedure for Single-
Axis Interferometric Fiber Optic Gyros", 1997.
 [26] IEEE Std 1293, "IEEE Standard Specification Format Guide and Test Procedure for Linear,
Single-Axis, Non-gyroscopic Accelerometers", 1998.
 [27] I. Skog and P. H¨ and el, "Calibration of a MEMS inertial measurement unit", in XVII IMEKO
World Congress, 2006.
 [28] Oliver J. Woodman," An introduction to inertial navigation". University of Cambridge 2007.
01/27/15 47

48. 01/27/15 48

49. 01/27/15 49