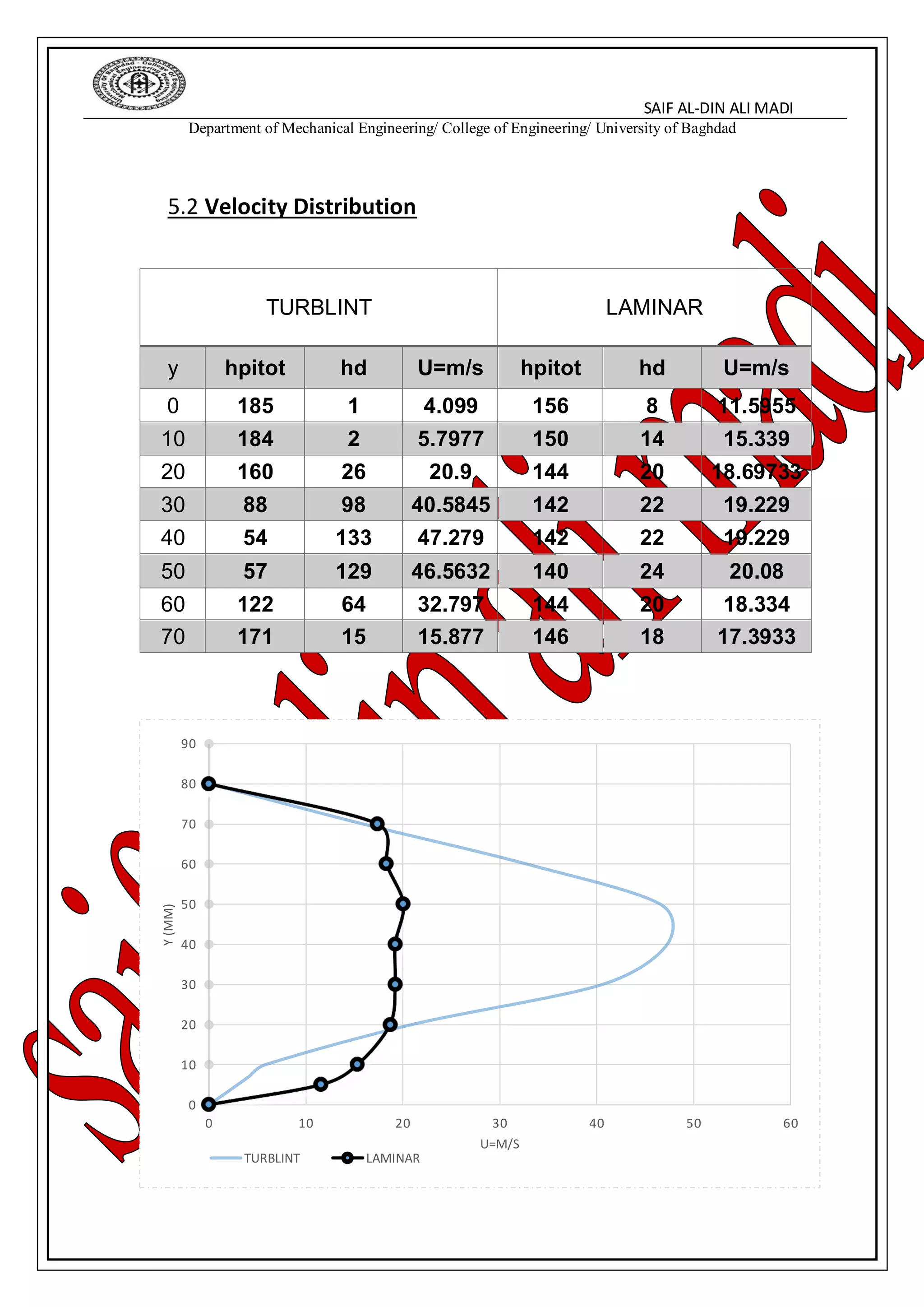
This document discusses fluid mechanics concepts and fluid flow measurement techniques. It begins with defining different types of fluid flows such as steady/unsteady, uniform/non-uniform, and laminar/turbulent flows. It then describes measuring techniques for pressure, including static, dynamic, and stagnation pressures. Common pressure measurement instruments like the U-tube manometer and pressure transducers are also introduced. The document concludes with discussing the boundary layer and formulas for calculating volume flow rate by measuring velocity and duct area.
![SAIF AL-DIN ALI MADI
Department of Mechanical Engineering/ College of Engineering/ University of Baghdad
[Fluid Laboratory II]
University of Baghdad](https://image.slidesharecdn.com/inducedflow-181109205459/75/Induced-flow-Fluid-Laboratory-U-O-B-1-2048.jpg)
















![SAIF AL-DIN ALI MADI
Department of Mechanical Engineering/ College of Engineering/ University of Baghdad
4.3 Discharge Flow Rate
Put the orifice meter in the pipe end to measurement compound flow rate
(secondary + primary), by using the following equation:
Qc = koc
𝛑𝐝𝐨𝐜 𝟐
𝟒
*75.1√
𝐓𝐚 𝐡𝐜
𝐏𝐚[𝟏−(
𝐝𝐨𝐜
𝐝
)
𝟒
]
By using available information you can obtain
Qc=0.231√
𝐓𝐚
𝐏𝐚
𝐡𝐜
Where
hc = orifice head in the end duct (mm)
The same method finds the primary flow rate (Qp):-
Qp=kop
𝛑𝐝𝐨𝐩 𝟐
𝟒
(75.1)√
𝐓𝐚
𝐏𝐚
(𝐡𝐩𝟐)
Qp=0.172√
𝐓𝐚
𝐩𝐚
(𝐡𝐩𝟐)
Where: hp orifice head in the start jet (mm).
4.4 Find the friction Force:-
1. Theoretical analysis
Re =
ρavaD
μa
μa = 1.8 × 10−5
m2
/s
ρa = 1.2 kg/m^3
F = 8TWdx
Ff = πD ∫ TW dx = πDTWl = (
π
8
1
0
)fpauc
2 Dl
Ff =
2fρa Qc
2
l
πD3](https://image.slidesharecdn.com/inducedflow-181109205459/75/Induced-flow-Fluid-Laboratory-U-O-B-18-2048.jpg)









![SAIF AL-DIN ALI MADI
Department of Mechanical Engineering/ College of Engineering/ University of Baghdad
v2 =
2pwg hd
fa 103
}/R
v2
R
=
2pwg hd
fa 103R
∵
Ta
Pa
=
1
pa
v2
R
=
2pwg hd
fa 103R
∗
Ta
𝛒 𝐚a
v = √
2 ∗ 1000 ∗ 9.81 ∗ 287
103
Ta
𝛒 𝐚
hd
v = 75.1√
Ta
𝛒 𝐚
hd
B. equation 5
Qc = kc
πdC
2
4
75.1√
Ta hc
ρa[1 − (
dC
2
D
)4]
Qc = 0.64 ∗
3.14(66 ∗ 10−3)2
4
∗ 75.1√
Ta hc
ρa[1 − (
66 ∗ 10−3
79 ∗ 10−3)4]
Qc =
0.6574
4
∗ √
Ta hc
ρa[0.5128]
Qc =
0.6574
4
∗ √
Ta hc
ρa[0.5128]
Qc =
0.6574
2.864
∗ √
Ta
ρa
hc
Qc = 0.231 ∗ √
Ta
ρa
hc](https://image.slidesharecdn.com/inducedflow-181109205459/75/Induced-flow-Fluid-Laboratory-U-O-B-29-2048.jpg)


