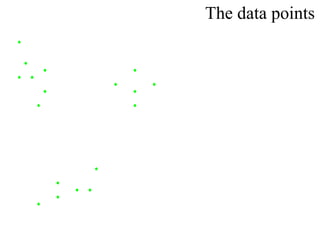
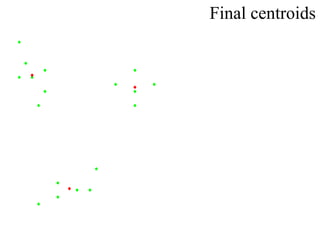
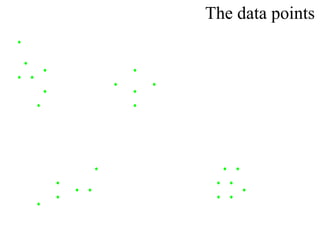
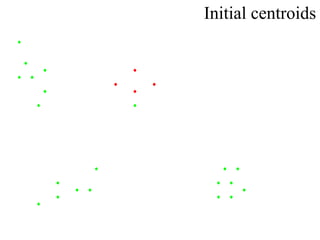
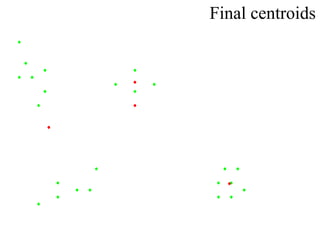
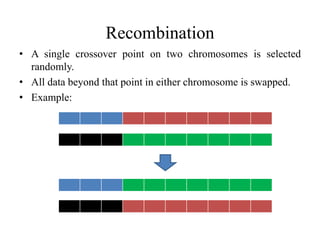
This document proposes using a genetic algorithm to improve the accuracy of k-means clustering by selecting better initial centroids. It describes generating an initial population of random centroids, evaluating their fitness using a k-means objective function, and evolving the population over generations using selection, crossover and mutation to converge on high-fitness initial centroids. Testing showed this genetic k-means approach produced more accurate and globally optimized clustering results than random initial centroids.

1. Improving the Accuracy of
K-means Algorithm
using
Genetic Algorithm
W. T. R. Fernando*
K. R. Wijeweera
D. M. N. K. Dasanayaka

2. K-means Algorithm Example 1

3. The data points

4. Initial centroids

5. Final centroids

6. K-means Algorithm Example 2

7. The data points

8. Initial centroids

9. Final centroids

10. Problem
• The accuracy of convergence depends on the level of
approximation of the initial centroids.
• A method is proposed to overcome this problem by
approximating the initial centroids using genetic algorithm.

11. Creating the Initial Population
• Suppose there are n number of points with k number of
clusters.
• A gene consists of coordinates of a point randomly picked
from the set of points.
• A chain of k number of such genes forms a chromosome.
• A collection of N number of such chromosomes forms the
initial population.
• An example chromosome:
(10, 15) (34, 17) (22, 57) (103, 82) (85, 94) (12, 94) (30, 48) (11, 72) (150, 63) (47, 88)

12. The Process of Evolution
• Selection
• Recombination
• Mutation

13. Selection
• The fitness of each chromosome is evaluated using a fitness
function.
• Let G be the average J(C) value of chromosomes.
• Then the fitness of a given chromosome is calculated by:
F = G/J(C);
• The chromosomes with higher fitness values should be
replicated.
• The chromosomes with lower fitness values should be
removed.

14. Recombination
• A single crossover point on two chromosomes is selected
randomly.
• All data beyond that point in either chromosome is swapped.
• Example:

15. Mutation
• Randomly select a gene in the chromosome.
• Replace the coordinates in that gene by a random point in the
set of points.

16. Results
• A random chromosome is picked from the final population and
used it for the initial centroids of k-means algorithm.
• The recombination between 45% - 65%, mutation between
10% - 14% and number of iterations (or populations created)
among 20-30 yields more accurate and globally optimized
results.

17. Any Questions?

18. Thank You!