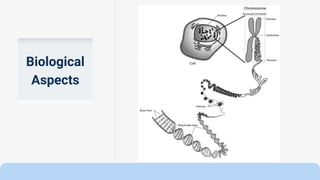
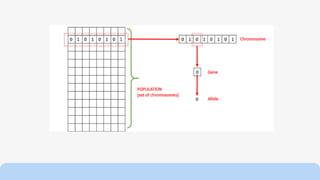
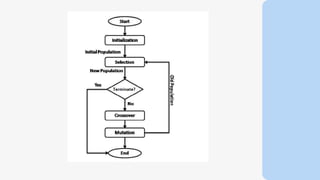
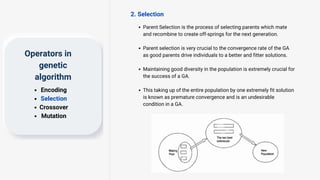
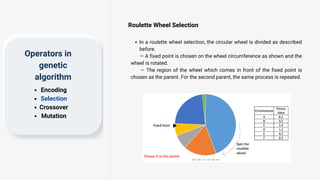
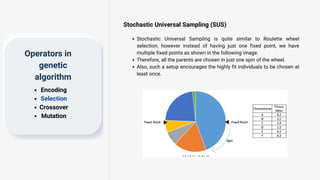
Genetic algorithms are a type of optimization technique based on principles of genetics and natural selection. They are commonly used to find optimal or near-optimal solutions to complex problems. A genetic algorithm works by generating an initial population of solutions randomly and then applying genetic operators like selection, crossover and mutation to produce new solutions over successive generations. The fittest solutions survive and less fit solutions are removed, causing the overall population to evolve toward an optimal solution. Key components of a genetic algorithm include encoding potential solutions, selecting parents for mating based on fitness, recombining parents to produce offspring, and introducing random mutations. Genetic algorithms terminate when a maximum number of generations is reached, a fitness threshold is met, or there is no improvement over successive generations

1. Genetic
Algorithm

2. Introduction
* Genetic Algorithm (GA) is a search-based
optimization technique based on the
principles of Genetics and Natural Selection.
* It is frequently used to find optimal or near-
optimal solutions to difficult problems which
otherwise would take a lifetime to solve.
* It is frequently used to solve optimization
problems, in research, and in machine
learning.

3. Biological
Aspects

4. Basic Terminology.
Population - It is a subset of all the possible solutions to the
given problem. The population for a GA is analogous to the
population for human beings except that instead of human
beings, we have Candidate Solutions representing human
beings.
Chromosomes - A chromosome is one such solution to the given
problem.
Gene - A gene is one element position of a chromosome.
Allele - It is the value a gene takes for a particular chromosome.

6. Terminology cntd...
Fitness Function - A fitness function simply
defined is a function which takes the solution as
input and produces the suitability of the solution
as the output.
Genetic Operators — These alter the genetic
composition of the offspring. These include
crossover, mutation, selection, etc.

7. We start with an initial population (which may be generated at random or seeded by other heuristics),
Select parents from this population for mating according to their fitness value.
Apply crossover and mutation operators on the parents to generate new off-springs.
And finally these off-springs replace the existing individuals in the population and the process repeats.
In this way genetic algorithms actually try to mimic the human evolution to some extent.
How GA works

9. BEGIN/* genetic algorithm"/
Generate initial population;
Compute fitness of each individual;
WHILE NOT finished DO LOOP
BEGIN
Select individuals from old generations
For mating;
Create offspring by applying
recombination and/or mutation
to the selected individuals;
Compute fitness of the new individuals;
Kill old individuals to make room for
new chromosomes and insert
offspring in the new generalization;
IF Population has converged
THEN finishes: =TRUE;
END
END
Algorithm

10. 1. Encoding
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Encoding is a process of representing individual genes. The process
can be performed using bits, numbers, trees, arrays, lists or any other
objects.
Each chromosome encodes a binary (bit) string. Each bit in the
string can represent some characteristics of the solution.
1.1. Binary Encoding

11. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
This encoding uses string made up of octal numbers (0-7).
1.2. Octal Encoding
1.3. Hexadecimal Encoding
This encoding uses string made up of hexadecimal numbers (0-9, A-F).
1.4. Permutation Encoding
Every chromosome is a string of integer/real values, which represents
number in a sequence. It is only useful for ordering problems.

12. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
1.5. Value Encoding
Every chromosome is a string of some values. Values can be anything
connected to problem, form numbers, real numbers or characters to
some complicated objects.
1.6. Tree Encoding
This encoding is mainly used for evolving program expressions for
genetic programming. Every chromosome is a tree of some objects such
as functions and commands of a programming language.

13. 2. Selection
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Parent Selection is the process of selecting parents which mate
and recombine to create off-springs for the next generation.
Parent selection is very crucial to the convergence rate of the GA
as good parents drive individuals to a better and fitter solutions.
Maintaining good diversity in the population is extremely crucial for
the success of a GA.
This taking up of the entire population by one extremely fit solution
is known as premature convergence and is an undesirable
condition in a GA.

14. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Fitness Proportionate Selection is one of the most popular ways of
parent selection.
In this every individual can become a parent with a probability
which is proportional to its fitness.
Therefore, fitter individuals have a higher chance of mating and
propagating their features to the next generation.
Therefore, such a selection strategy applies a selection pressure to
the more fit individuals in the population, evolving better
individuals over time.
Two methods
— Roulette Wheel Selection
— Stochastic Universal Sampling (SUS)
Fitness Proportionate Selection

15. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
In a roulette wheel selection, the circular wheel is divided as described
before.
— A fixed point is chosen on the wheel circumference as shown and the
wheel is rotated.
— The region of the wheel which comes in front of the fixed point is
chosen as the parent. For the second parent, the same process is repeated.
Roulette Wheel Selection

16. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Calculate S = the sum of a finesses.
Generate a random number between 0 and S.
Starting from the top of the population, keep adding the finesses to the
partial sum P, till P<S.
The individual for which P exceeds S is the chosen individual.
It is clear that a fitter individual has a greater pie on the wheel and therefore
a greater chance of landing in front of the fixed point when the wheel is
rotated. Therefore, the probability of choosing an individual depends
directly on its fitness.
Implementation wise, we use the following steps −
.
Random Selection
In this strategy we randomly select parents from the existing population.

17. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Stochastic Universal Sampling is quite similar to Roulette wheel
selection, however instead of having just one fixed point, we have
multiple fixed points as shown in the following image.
Therefore, all the parents are chosen in just one spin of the wheel.
Also, such a setup encourages the highly fit individuals to be chosen at
least once.
Stochastic Universal Sampling (SUS)

18. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
In K-Way tournament selection, we select K individuals from the
population at random and select the best out of these to become a
parent.
The same process is repeated for selecting the next parent.
Tournament Selection is also extremely popular in literature as it can
even work with negative fitness values.
Tournament Selection

19. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Rank Selection also works with negative fitness values and is mostly
used when the individuals in the population have very close fitness
values (this happens usually at the end of the run).
This leads to each individual having an almost equal share of the pie
(like in case of fitness proportionate selection) as shown in the
following image and hence each individual no matter how fit relative to
each other has an approximately same probability of getting selected
as a parent.
This in turn leads to a loss in the selection pressure towards fitter
individuals, making the GA to make poor parent selections in such
situations.
Rank Selection

20. 3. Crossover/ Recombination
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Crossover is the process of taking two parent solutions and
producing from them a child.
After the selection (reproduction) process, the population is
enriched with better individuals.
Crossover operator is applied to the mating pool with the hope
that it creates a better offspring.
Crossover is a recombination operator that proceeds in three
steps:
The reproduction operator selects at random a pair of two
individual strings for the mating.
A cross site is selected at random along the string length.
Finally, the position values are swapped between the two
strings following the cross sites.
1.
2.
3.

21. 3.1 Single-point Crossover
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
A random crossover point is selected and the tails of its two parents
are swapped to get new off-springs.
3.2 Two-point Crossover
Two crossover points are chosen and the contents between these
points are exchanged between two mated parents.

22. 3.3 Multi-point Crossover
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
There are two ways in this crossover.
In the case of even number of cross sites, the cross sites are selected
randomly around a circle and information is exchanged.
In the case of odd number of cross sites, a different cross point is
always assumed at the string beginning.
--- One is even number of cross sites and the other odd number of
cross sites.
3.4 Uniform Crossover
Each gene in the offspring is created by copying the corresponding
gene from one or the other parent chosen according to a random
generated binary crossover mask of the same length as the
chromosomes.

23. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Where there is a 1 in the crossover mask, the gene is copied from the
first parent, and where there is a 0 in the mask the gene is copied
from the second parent
3.5 Three-parent Crossover
In this crossover technique, three parents are randomly chosen.
Each bit of the first parent is compared with the bit of the second
parent.
lf both are the same, the bit is taken for the offspring, otherwise
the bit from the third parent is taken for the offspring.
Child 1 and mask 1 -> -Parent 1
Child 1 and mask 0 -> -Parent 2
Child 2 and mask 1 -> -Parent 2
Child 2 and mask 0 -> -Parent 1

24. 3.6 Crossover with Reduced Surrogate
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
The reduced surrogate operator constraints crossover to always
produce new individuals wherever possible.
This is implemented by restricting the location of crossover points
such that crossover points Only occur where gene values differ.
3.7 Shuffle Crossover
Shuffle crossover is related to uniform crossover.
A single crossover position (as in single-point crossover) is
selected.
But before the variables are exchanged, they are randomly shuffled
in both parents.
After recombination, the variables in the offspring are unshuffled.
This removes positional bias as the variables are randomly
reassigned each time crossover is performed.
3.8 Precedence Preservative Crossover
It was developed for vehicle routing problems and scheduling
problems.

25. Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
First we start by initializing an empty offspring.
The leftmost operation in one of the two parents is selected in
accordance with the order of parents given in the vector.
After an operation is selected, it is deleted in both parents.
Finally the selected operation is appended to the offspring.
Step 4. is repeated until both parents are empty and the offspring
contains all operations involved.
1.
2.
3.
4.
5.
3.9 Ordered Crossover
Given two parent chromosomes, two random crossover points are
selected partitioning them into left, middle and right portions.
child 1 inherits its left and right section from parent 1, and its
middle section is determined by the genes in the middle section of
parent 1 in the order in which the values appear in parent 2.
A similar process is applied to determine child 2.

26. The two chromosomes are aligned.
Two crossing sites are selected uniformly at random along the
strings, defining a matching section.
The matching section is used to effect a cross through position-
by-position exchange operation.
Alleles are moved to their new positions in the offspring.
1.
2.
3.
4.
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
3.10 Partially Matched Crossover

27. The two chromosomes are aligned.
Two crossing sites are selected uniformly at random along the
strings, defining a matching section.
The matching section is used to effect a cross through position-
by-position exchange operation.
Alleles are moved to their new positions in the offspring.
1.
2.
3.
4.
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
3.10 Partially Matched Crossover
5<->2 6<->3 7<->10

28. Crossover probability is a parameter to describe how often
crossover will be performed.
If there is no crossover, offspring are exact copies of parents.
If there is crossover, offspring are made from part of both
parents' chromosome.
If crossover probability is 100%, then all offspring are made by
crossover.
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Crossover Probability(P꜀)

29. Mutation
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Mutation may be defined as a small random tweak in the
chromosome, to get a new solution.
After crossover, the strings are subjected to mutation.
Mutation has been traditionally considered as a simple search
operator.
Mutation helps escape from local minimal trap and maintains
diversity in the population.
It also keeps the gene pool well stocked.

30. 4.1 Flipping
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
Flipping of a bit involves changing 0 to 1 and 1 to 0 based on a
mutation chromosome generated.
For a 1 in mutation chromosome, the corresponding bit in parent
chromosome is flipped (0 to 1 and 1 to 0) and child chromosome
is produced.
4.2 Interchanged
Two random positions of the string are chosen and the bits
corresponding to those positions are interchanged.

31. 4.3 Reversed
Operators in
genetic
algorithm
Encoding
Selection
Crossover
Mutation
A random position is chosen and the bits next to that position are
reversed and child chromosome is produced
Mutation Probability(Pₘ)
It decides how often parts of chromosome will be mutated.
If there is no mutation, offspring are generated immediately after
crossover without any change.
If mutation is performed, one or more parts of a chromosome are
changed.
If mutation probability is 100%, whole chromosome is changed.

32. Stopping condition for genetic
algorithm
1. Maximum generations
The GA stops when the specified number of
generations has evolved
2. Elapsed time
The generic process will end when a specified time has
elapsed. If the maximum number of generation has
been reached before the specified time has elapsed, the
process will end.
3. No change in fitness
The genetic process will end if there is no change
to the population's best fitness for a specified
number of generations.
4. Stall generations
The algorithm stops if there is no improvement in the
objective function for a sequence of consecutive
generations of length "Stall generations".
5. Stall time limit.
The algorithm stops if there is no improvement in the objective
function during an interval of time in seconds equal to "Stall time
limit.

33. Methods of termination
techniques.
Best Individual - A best individual convergence
criterion stops the search once the minimum fitness
in the population drops below the convergence value.
This brings the search to a faster conclusion,
guaranteeing at least one good solution.
Worst Individual - Worst individual terminates the
search when the least fit individuals in the population
have fitness less than the convergence criteria.
Sum of Fitness - The search is considered to have
satisfaction converged when the sum of the fitness in
the entire population is less than or equal to the
convergence value in the population record.
Median Fitness - Here at least half of the individuals
will be better than or equal to the convergence value,
which should give a good range of solutions to
choose from.

34. Thank you!