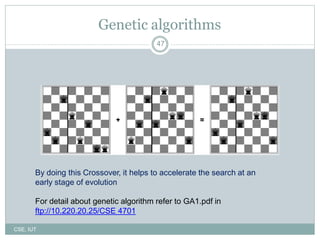
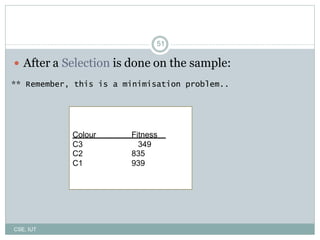
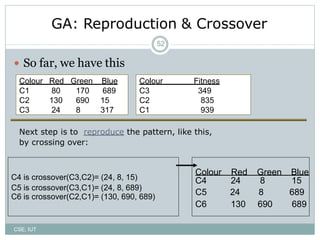
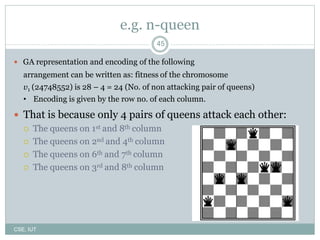
The document describes genetic algorithms, which are inspired by biological evolution. It discusses how genetic algorithms work by starting with a random population that undergoes selection, crossover, and mutation to generate new solutions. The population evolves over multiple generations as higher-fitness solutions are more likely to be selected for reproduction and combination with other solutions. This evolutionary process can help search large problem spaces to find optimal or near-optimal solutions.

1. Genetic Algorithm

2. 40
states
(often encoded as a string of 0s and 1s)
better states.
crossover, and mutation
Genetic/ Evolutionary algorithms
 Developed by John Holland in 1975
 inspired by biological mutation & evolution
 stochastic (means non-deterministic) search techniques
based on the mechanism of natural selection and genetics
 A successor state is generated by combining two parent
 Start with k randomly generated states (population)
 A state is represented as a string over a finite alphabet
 Evaluation function (fitness function). Higher values for
 Produce the next generation of states by selection,
CSE, IUT

3. 43
“Select The Best, Discard The Rest”
 fitness function is upto user (problem specific)-
means to evaluate the potential of a candidate in
the population. e.g. for a binary representation
fitness function could be:
 f(i) = ∑i f(i) ;where i is from 1 to l (l=total length of the sequence)
 And in the selection step, the probability of getting
selection for a candidate is:
 Prob i = f(i) / ∑i f(i)
CSE, IUT

4. 44
Encoding
The process of representing the solution in the form of a string that
conveys the necessary information.
 Binary Encoding – Most common method of encoding.
Chromosomes are strings of 1s and 0s and each position in the
chromosome represents a particular characteristic of the problem.
Permutation Encoding – Useful in ordering problems such as the
Traveling Salesman Problem (TSP). Example. In TSP, every
chromosome is a string of numbers, each of which represents a city to
be visited.
 Value Encoding – Used in problems where complicated values, such
as real numbers, are used and where binary encoding would not suffice.
CSE, IUT

5. 45
e.g. n-queen
 GA representation and encoding of the following
arrangement can be written as: fitness of the chromosome
v1 (24748552) is 28 – 4 = 24 (No. of non attacking pair of queens)
• Encoding is given by the row no. of each column.
 That is because only 4 pairs of queens attack each other:
 The queens on 1st and 8th column
 The queens on 2nd and 4th column
 The queens on 6th and 7th column
 The queens on 3rd and 8th column
CSE, IUT

6. 46
Genetic algorithms
 Fitness function: number of non-attacking pairs of queens
(min = 0, max = 8c2 excluding same pair = 28)
 24/(24+23+20+11) = 31%

 23/(24+23+20+11) = 29% etc
 Here single point crossover & mutation occurred
CSE, IUT

7. 41
Genetic/ Evolutionary algorithms
 Outline of the Basic Genetic Algorithm
1 [Start] Generate random population of n chromosomes (suitable solutions for the
problem)
2 [Fitness] Evaluate the fitness f(x) of each chromosome x in the population
3 [New population] Create a new population by repeating following steps until the new
population is complete
 [Selection] Select two parent chromosomes from a population according to their
fitness (the better fitness, the bigger chance to be selected)
 [Crossover] With a crossover probability cross over the parents to form a new
offspring (children). If no crossover was performed, offspring is an exact copy of
parents.
 [Mutation] With a mutation probability mutate new offspring at each locus (position
in chromosome).
 [Accepting] Place new offspring in a new population (keep population size constant)
4 [Replace] Use new generated population for a further run of algorithm
5 [Test] If the end condition is satisfied, stop, and return the best solution in current
population
 [Loop] Go to step 3
CSE, IUT

8. 41
Genetic/ Evolutionary algorithms
CSE, IUT

9. 47
Genetic algorithms
By doing this Crossover, it helps to accelerate the search at an
early stage of evolution
For detail about genetic algorithm refer to GA1.pdf in
ftp://10.220.20.25/CSE 4701
CSE, IUT

10. 48
Another Example
(Assignment 1: Deadline 15 Feb, 2018)
 Data population: RGB colours
 Aim: to obtain darkest colour represented by
(0, 0, 0)
 This is a minimisation problem, i.e. a good
colour is one that fits for (colour) --> 0.
 We now tabulate our data as shown
CSE, IUT

11. 49
 Start at a random pattern like this:
Colour Red Green Blue
C1 80 170 689
C2 130 690 15
C3 24 8 317
where
Fitness for (C1) = 80 + 170 + 689 = 939
Fitness for (C2) = 130 + 690 + 15 = 835
Fitness for (C3) = 24 + 8 + 317 = 349
CSE, IUT

12. 50
Fitness (C2) = 130 + 690 + 15 = 835
C1
 Start at a random pattern like this:
Colour Red Green Blue
C1 80 170 689
C2 130 690 15
C3 24 8 317
FITTEST
PLACED TOP
C3
Fitness (C1) = 80 + 170 + 689 = 939
C2
Fitness (C3) = 24 + 8 + 317 = 349
CSE, IUT

13. 51
 After a Selection is done on the sample:
** Remember, this is a minimisation problem..
Colour Fitness
C3 349
C2 835
C1 939
CSE, IUT

14. 52
C4 24 8 15C4 is crossover(C3,C2)= (24, 8, 15)
C6 is crossover(C2,C1)= (130, 690, 689)
GA: Reproduction & Crossover
 So far, we have this
Colour Red Green Blue Colour Fitness
C1 80 170 689 C3 349
C2 130 690 15 C2 835
C3 24 8 317 C1 939
Next step is to reproduce the pattern, like this,
by crossing over:
Colour Red Green Blue
C5 is crossover(C3,C1)= (24, 8, 689)
C5 24 8 689
C6 130 690 689
CSE, IUT

15. 53
 perform mutation, and we have
C7 is obtained by mutating(4) =(24, 8, 13)
C8 is obtained by mutating(5) =(25, 9, 689 )
C9 is obtained by mutating(6) =(128, 688, 689)
Colour Red Green Blue
New population of C7 24 8 13
3 chromosomes C8 25 9 689
C9 128 688 689
CSE, IUT

16. 54
Conclusion (up to “mutation” to get a new data set)
 Some solutions have improved (after first iteration):
Getting better rather fast
Slightly improved of the answer
Fitness for C7 = (24 + 8 + 13) = 45
Fitness for C8 = (25 + 9 + 689) = 743
Fitness for C9 = (128 + 688 + 689 ) = 1505
If the process is iterated, population will converge to
have fitness near to zero (colour) --> 0.
Continue..............
CSE, IUT