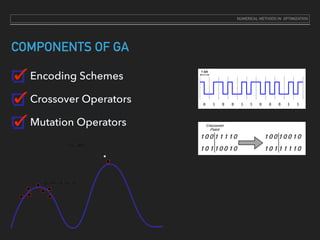
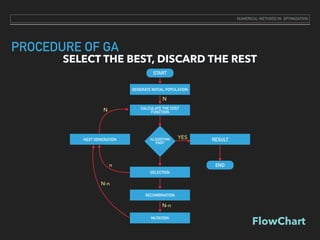
This document discusses genetic algorithms and their use for optimization problems. It begins by defining genetic algorithms as search and optimization techniques based on Darwin's principle of natural selection. It then outlines the components and working of genetic algorithms, including encoding potential solutions as chromosomes, selecting chromosomes based on their fitness, and generating new solutions through crossover and mutation of parents. The document provides an example problem of using genetic algorithms to generate mathematical expressions that equal a target value.

1. GENETIC ALGORITHM
FOR OPTIMIZATION
FETHİ CANDAN
ANIL ERDİNÇ TÜFEKÇİ
İSMAİL HANCI

2. NUMERICAL METHODS IN OPTIMIZATION
OUTLINE
▸ What are the Genetic Algorithms (GA)
▸ Characteristics of GA
▸ Darwin’s Principle of Natural Selection
▸ Working of GA
▸ Components of GA
▸ Uniqueness of GA
▸ Procedure of GA
▸ Example

3. WHAT ARE THE GENETIC ALGORITHMS
Genetic Algorithms are search and optimization techniques
based on Darwin’s Principle of Natural Selection.
NUMERICAL METHODS IN OPTIMIZATION

4. HISTORY OF GA
▸ 1950 : Alan Turing proposed a “Learning Machine”
▸ 1957 : Alex Fraser published simulation of artificial
selection of organisms
▸ 1960 : Hans-Joachim Bremermann published a
series of papers in the 1960s that also adopted a
population of solution to optimization problems,
undergoing recombination, mutation, and
selection. Bremermann's research also included the
elements of modern genetic algorithms.
▸ 1975 : J.H.Holland, Adaptive in Natural and
Artificial Systems.
NUMERICAL METHODS IN OPTIMIZATION

5. CHARACTERISTICS OF GA
▸ Stochastic in nature and less likely to get caught in local minima, so
mostly used for global optimization problems
▸ Applies to both continuous and discrete optimization problems
▸ Parallel-Search procedure that can be implemented on parallel
processing machines for speeding operations
▸ Heuristic method based on ‘Survival of the fittest’
▸ Useful when search space very large or too complex for analytic
treatment
NUMERICAL METHODS IN OPTIMIZATION

6. DARWIN’S PRINCIPLE OF NATURAL SELECTION
The basic principles formulated by Darwin:
1.The strongest survive and tips die (Natural Selection)
2.The new individual is obtained by crossing and there is
mutation
NUMERICAL METHODS IN OPTIMIZATION

7. WORKING GA
▸ GA encodes each point in a parameter space into a binary bit
called chromosome
▸ Each point is associated with a fitness function
▸ Gene pool is a population of all such points
▸ In each generation GA constructs a new population using
genetic operators
Crossover
Mutation
NUMERICAL METHODS IN OPTIMIZATION

8. COMPONENTS OF GA
Encoding Schemes
Crossover Operators
Mutation Operators
NUMERICAL METHODS IN OPTIMIZATION

9. STOCHASTIC OPERATORS
▸ Selection : Replicates the most successful solutions found
in a population at a rate proportional to their relative
quality.
▸ Recombination : Decomposes two distinct solution and
then randomly mixes their parts to form new solutions.
▸ Mutation : Randomly pertubs a candidate solution.
NUMERICAL METHODS IN OPTIMIZATION

10. UNIQUENESS OF GA
▸ Works with a coding of the parameter set, not the
parameter themselves
▸ Search for a population of point and not single point
▸ Use objective function information and not derivatives or
other auxiliary knowledge
NUMERICAL METHODS IN OPTIMIZATION

11. PROCEDURE OF GA
FlowChart
SELECT THE BEST, DISCARD THE REST
START
GENERATE INITIAL POPULATION
CALCULATE THE COST
FUNCTION
ALGORITHM
END?
SELECTION
RECOMBINATION
MUTATION
NEXT GENERATION RESULT
END
N
N-n
n
N-n
N
YES
NUMERICAL METHODS IN OPTIMIZATION

12. EXAMPLE
• A simple GA application
• Problem : Reach a target value with simple mathematical calculations.
• We have a target value such as 5, 37, 72.8, 231.38, etc.
• We have numbers { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }.
• We have operators { +, -, *, / }
• Totally we have 14 (10 + 4) different elements.
• We call each of one as GENE.
• A combination of GENEs, becomes a CHROMOSOME.
NUMERICAL METHODS IN OPTIMIZATION

13. ▸ We have to encode all of these different genes
▸ As a general attitude, we use binary bits
▸ Binary bits string
▸ The number of different elements that can be encoded:
▸ We have to chose bit number n so as to have enough space for
encoding all our different
NUMERICAL METHODS IN OPTIMIZATION

14. We can encode our elements as such:
NUMERICAL METHODS IN OPTIMIZATION

15. ▸ Problem (Mathematical Calculations) can be formulated differently
▸ Prob1 : use each number ones
▸ Prob2 : use each operator ones
▸ Prob3 : use each number ones, but there is no restriction about
operators
▸ Prob4 : use operator ones, but there is no restriction about numbers
▸ There may be Restrictions on number of elements or Gene. It defines the
length of chromosomes.
▸ Chromosome Length = Gene Length x Number of Genes
NUMERICAL METHODS IN OPTIMIZATION

16. Target
Genes
Chromosome
NUMERICAL METHODS IN OPTIMIZATION

17. ‣ We need to decide some parameters beforehand.
‣ Later according to performance, we have to change these
parameters to improve the performance considering our
restrictions such as
‣ Convergence ratio
‣ Computation number
‣ Computation types
‣ Storage, RAM, time, error tolerance (fitness score and target)…
NUMERICAL METHODS IN OPTIMIZATION

18. GA DESIGN PARAMETERS
‣ Number of POPULATION
‣ Length of CHROMOSOME
‣ Value and type of CROSSOVER
‣ Value of MUTATION RATE
‣ Number of GENERATIONS (stop criteria)
‣ Type of SELECTION
NUMERICAL METHODS IN OPTIMIZATION

19. ‣ Population (parents, fathers and mothers)
‣ Population number can be 500, 20.000, or 1.000.000
‣ We create randomly
NUMERICAL METHODS IN OPTIMIZATION

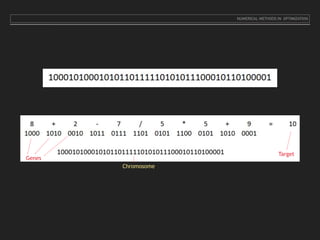
20. ‣ We test each population member for a possible solution to the problem.
‣ We decode each gene with the order.
‣ Calculate the result mathematically ( 8 + 5 – 3 / 2 *4 / 7 = 2.857)
‣ We need to define a Fitness Score for each member of population in
every generation.
‣ It is normalized to [0 , 1].
NUMERICAL METHODS IN OPTIMIZATION

21. ▸ Fitness Score Calculation or Fitness Function
▸ There can be different calculations
▸ One of them is
|Target Value - Result|
1_____________________
NUMERICAL METHODS IN OPTIMIZATION

22. ‣ After assigning a Fitness Score to each population, we have to
eliminate weak ones as nature does due to Darwin’s Natural
Selection Principle
‣ We need a Selection Pattern
‣ One method is Roulette Wheel
NUMERICAL METHODS IN OPTIMIZATION

23. ‣ We define a crossover pattern.
‣ In nature, we have dominant and recessive genes.
‣ We model with random numbers.
‣ The aim of crossover is to sustain different members, chormosomes or solution
variables.
‣ If the same population we cannot find the solution.
‣ We have to mix population by Crossover
NUMERICAL METHODS IN OPTIMIZATION

24. ‣ We define a mutatation pattern
‣ As it is also rare in nature, we have low mutation ratio
‣ The aim of mutation is sustain different members as well
NUMERICAL METHODS IN OPTIMIZATION

25. THANKS FOR LISTENING… ANY QUESTIONS ?
NUMERICAL METHODS IN OPTIMIZATION