Basic MATLAB-Presentation.pptx

Presentation on Base MATLAB®
Premanand S
Assistant Professor
newgen.anand@gmail.com
+91 9443917210

What is MATLAB ?
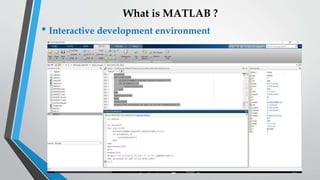
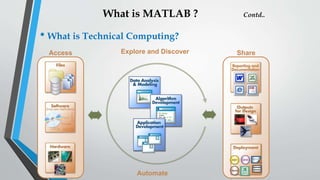
• Interactive development environment

What is MATLAB ? Contd..
• Technical computing language-
- Millions of engineers and scientists worldwide use MATLAB®.
- To analyse and design the systems and products.
• It is used for,
-Machine learning, -Signal processing,
-Image processing, - Computer vision,
-Communications, -Computational finance,
-Control design, - Robotics.

Data Analysis and Visualization-

• Algorithm Development

• Application Deployment

• What is Technical Computing?
Explore and Discover
Automate
Access Share

• The basic arithmetic operators are
+ - * / ^
• The symbol ^ is used to get exponents (powers): 2^4=16.
For e.g. 2 + 3/4*5
ans =
5.7500.
Que. Is this ans for 2+(3/4)*5 or 2+3/(4*5) ?
MATLAB works according to the priorities:
1. quantities in brackets,
2. powers 2 + 3^2 ⇒2 + 9 = 11,
3. * /, working left to right (3*4/5=12/5),
4. + -, working left to right (3+4-5=7-5),

03-08-2022 04:28 14
MATLAB recognizes several diﬀerent kinds of numbers

03-08-2022 04:28 15
The format — how MATLAB prints numbers —is controlled
by the “format” command.
Type help format for full list.
The command
>>format compact

03-08-2022 04:28 17
(1) 3-2^4 ans = -13.
(2) ans*5 ans =-65.
The result of the ﬁrst calculation is labelled “ans” by MATLAB and is used
in the second calculation where its value is changed.
• We can use our own names to store numbers:
(1) x = 3-2^4 ; x = -13
(2) y = x*5 ; y =-65
These are examples of assignment statements: Values are assigned to
variables. Each variable must be assigned a value before

03-08-2022 04:28 18
Legal names of variables consist of any combination of letters and
digits, starting with a letter.
These are allowable: NetCost, Left2Pay, x3, X3, z25, c5.
These are not allowable: Net-Cost, 2pay, %x, @sign
Use names that reﬂect the values they represent.
If you wish to do arithmetic with complex numbers Both i and j have
the value √−1 unless you change them

03-08-2022 04:28 19
Exercise:
In each case ﬁnd the value of the expression in MATLAB and explain
precisely the order in which the calculation was performed.
i) -2^3+9
ii) 2/3*3
iii) 3*2/3
iv) 3*4-5^2*2-3
iv) 3*4-5^2*2-3
v) (2/3^2*5)*(3-4^3)^2 vi) 3*(3*4-2*5^2-3)

03-08-2022 04:28 21
Trigonometric Functions
Function known to MATLAB are sin, cos, tan and their arguments
should be in radians.
The inverse trig functions are called asin, acos, atan The result is in
radians.

03-08-2022 04:28 22
Other Elementary Functions:
• These include sqrt, exp, log, log10.
• exp(x) denotes the exponential function exp(x) = ex.
• The inverse function is log.

03-08-2022 04:28 24
These come in two flavors (1) Row vectors (2) Column Vectors.
(1) Row vectors
• Lists of numbers separated by either commas or spaces.
• The number of entries is known as the “length” of the vector.
• The entries are often referred to as “elements” or “components”
• The entries must be enclosed in square brackets.
Vectors

03-08-2022 04:28 25
• We can do certain arithmetic operations with vectors of the same
length.
• A vector may be multiplied by a scalar (a number), or
added/subtracted to another vector of the same length.
• The operations are carried out element wise.
Vectors contd..

03-08-2022 04:28 26
The Colon Notation:
• This is a shortcut for producing row vectors:
• More generally a : b : c produces a vector of entries starting with the
value a, incrementing by the value b until it gets to c.
Extracting Bits of a Vector
• We can extract any bit of the vector.

03-08-2022 04:28 27
Column Vectors
• These have similar constructs to row vectors. When deﬁning
them, entries are separated by ; or “newlines”
• So column vectors may be added or subtracted provided that they
have the same length.
• We can convert a row vector into a column vector (and vice
versa) by a process called transposing—denoted by ’.

03-08-2022 04:28 28
Defining Complex Vector
• If x is a complex vector, then x’ gives the complex conjugate
transpose of x.
• The variable i has a numeric value.

03-08-2022 04:28 30
• Example: Plot a graph of y = sin 3πx for 0 ≤ x ≤ 1.
We do this by sampling the function at a suﬃciently large number of
points and then joining up the points (x, y) by straight lines. Suppose
we take N + 1 points equally spaced a distance h apart:

03-08-2022 04:28 31
Plotting—Titles & Labels:
To put a title and label the axes we use- title, xlabel & ylabel.
Grids:
A dotted grid may be added by
- grid
- grid off
Line Styles & Colors:
The default is to plot solid lines.
Hold
To stop the window being cleared:
>> plot(x,y,’w-’), hold
>> plot(x,y,’gx’), hold off

03-08-2022 04:28 32
Subplot
The graphics window may be split into an m × n array of smaller
windows into which we may plot one or more graphs.

Products, Division & Powers of Vectors

03-08-2022 04:28 34
Scalar Product (*)
The scalar product is deﬁned by multiplying the corresponding elements
together and adding the results to give a single number (scalar).
For example, if u = [10, −11, 12], and v =
𝟐𝟎
−𝟐𝟏
−𝟐𝟐
then n = 3 and
uv = 10 × 20 + (−11) × (−21) + 12 × (−22) = 167
We can perform this product in MATLAB by
u = [ 10, -11, 12], v = [20; -21; -22]

03-08-2022 04:28 35
Dot Product (.*)
• If u and v are two vectors of the same type (both row vectors or both column
vectors).
𝑢. 𝑣 = [𝑢1𝑣1 𝑢2𝑣2 … … 𝑢𝑛𝑣𝑛 ]
• The result is a vector of the same length. Thus, we simply multiply the
corresponding elements of two vectors.

03-08-2022 04:28 36
Example: Tabulate the function y = xsinπx for x = 0, 0.25, . . . , 1

03-08-2022 04:28 37
Dot Division of Arrays (./)
• In MATLAB, the operator ./ is deﬁned to give element by element division.
• It is therefore only deﬁned for vectors of the same size and type.
Dot Power of Arrays (.^)
• However, a neater way is to use the .^ operator:

03-08-2022 04:28 39
Example:
Draw graphs of the functions
i) 𝑦 =
sin 𝑥
𝑥
ii) 𝑢 =
1
(𝑥−1)2 − 𝑥
iii) 𝑣 =
𝑥2+1
𝑥2−4
iv) 𝑤 =
(10−𝑥)1/3−2
(4−𝑥2)1/2
for 0 ≤ x ≤ 10.

Matrices—Two–Dimensional
Arrays

03-08-2022 04:28 42
Size of a matrix:
• We can get the size (dimensions) of a matrix with the command size
• For e.g. size(A), size(x)

03-08-2022 04:28 43
Transpose of a matrix:
• Transposing a vector changes it from a row to a column vector and
vice versa.
• Idea: The 1st row becomes the 1st column, and so on.
>> D, D’
>> size(D), size(D’)

03-08-2022 04:28 44
Special Matrices:
• MATLAB provides a number of useful built–in matrices of any desired size.
• ones(m, n) gives an m × n matrix of 1’s,
>> P = ones(2,3)
• zeros(m, n) gives an m× n matrix of 0’s,
>> Z = zeros(2,3)
0 0 0
0 0 0
>> Z = zeros(size(P’))
ans =
0 0
0 0
0 0
The second command illustrates how we can construct a matrix based on the size of an
existing one. Try ones(size(D)).

03-08-2022 04:28 45
The Identity Matrix:
• The n × n identity matrix is a matrix of zeros except for having ones along
its leading diagonal (top left to bottom right).
Diagonal Matrices
• A diagonal matrix is similar to the identity matrix except that its
diagonal entries are not necessarily equal to 1.
Building Matrices:
• It is often convenient to build large matrices from smaller ones:

03-08-2022 04:28 46
Extracting Bits of Matrices
• We may extract sections from a matrix in much the same way as for a vector.
• Each element of a matrix is indexed according to which row and column it
belongs to.
• The entry in the ith row and jth column is denoted mathematically by Ai, j and, in
Matlab, by A(i,j).

03-08-2022 04:28 48
Loops
• If operation demands same operation to repeat no of times we use loop.
• Example: Draw graphs of sin(nπx) on the interval −1 ≤ x ≤ 1 for n = 1, 2, . . . , 8.
We could do this by giving 8 separate plot commands but it is much easier
to use a loop. The simplest form would be

03-08-2022 04:28 49
1) for a = 10:20
fprintf('value of a: %dn', a);%Display text variable
end
2) for a = 1.0: -0.1: 0.0;% for continuous elements.
disp(a)
end
3) for a = [24,18,17,23,28]
disp(a)
end
Create a script file and type the following code

03-08-2022 04:28 51
• MATLAB represents true and false by means of the integers 0 and 1.
true = 1, false = 0
• If at some point in a calculation a scalar x, say, has been assigned a value, we
may make certain logical tests on it:
x == 2 is x equal to 2?
x ~= 2 is x not equal to 2?
x > 2 is x greater than 2?
x < 2 is x less than 2?
x >= 2 is x greater than or equal to 2?
x <= 2 is x less than or equal to 2?

Function m–ﬁles
03-08-2022 04:28 52

03-08-2022 04:28 53
These are a combination of the ideas of script m–files and mathematical
functions.
The main steps to follow when defining a Matlab function are:
1. Decide a name for the function, making sure that it does not conflict
with a name that is already used by Matlab.
2. The first line of the file must have the format:
function [list of outputs] = function name(list of inputs)
3. For our example, the output (A) is a function of the three variables
(inputs) a, b and c so the first line should read
function [A] = area(a, b, c)

03-08-2022 04:28 54
4. Document the function.
5. Lines should be preceded by % which signify that they are comment lines
that will be ignored when the function is evaluated.
6. Finally include the code that deﬁnes the function.

03-08-2022 04:28 56
Execution:
Inputs:
a, b, c: Lengths of sides
Output:
A: area of triangle
Usage:
Area = area(define the value of a, b & c);

Simulink
• Simulink is a software package for modeling,
simulating, and analyzing dynamical systems
•Block diagram editing
•Nonlinear simulation
•Hybrid (continuous and discrete) models
•Asynchronous (non-uniform sampling) simulation
•Fully integrated with MATLAB, MATLAB toolboxes and
block sets.

Simulink
• Accurately design, implement, and test:
• Control systems
• Signal Processing systems
• Communications systems
• Embedded systems
• Physical systems
• other Dynamical systems

03-08-2022 04:28 61
www.mathworks.com
support
Documentation
https://in.mathworks.com/academia/student_center/tutorials.html?s_tid=acmain_st-pop-
tut_gw_bod

1
Presentation on MATLAB
Suraj Gawande
Engineer-Technical Support - Mathworks

What is MATLAB?
 High-level language
64

What is MATLAB?
 Interactive development environment
65

What is MATLAB?
 Interactive development environment
 Used for:
– Numerical computation
– Data analysis and visualization
– Algorithm development and programming
– Application development and deployment
66

Technical Computing Workflow
Reporting and
Documentation
Outputs for Design
Deployment
Share
Explore & Discover
Data Analysis
& Modeling
Algorithm
Development
Application
Development
Software
Hardware
Access
Files
Code & Applications
Automate 67

Accessing Data from MATLAB
 Files
– Excel, text, or binary
– Audio and video, image
– Scientific formats and XML
Explore & Discover Share
Access
68

 Files
– Excel, text, or binary
– Audio and video, image
– Scientific formats and XML
 Web Services
– JSON, CSV, and image data
– Financial Datafeeds (Datafeed T
oolbox)
Access
69

 Applications and languages
– C/C++, Java, FORTRAN
– COM, .NET
, shared libraries
– Databases (Database Toolbox)
Access
70

 Applications and languages
– C/C++, Java, FORTRAN
– COM, .NET
, shared libraries
– Databases (Database Toolbox)
 Measurement hardware
– Data acquisition hardware (Data Acquisition T
oolbox)
– Stand-alone instruments and devices
(Instrument Control T
oolbox)
Access
71

Data Analysis and Visualization in MATLAB
 Built-in engineering and
mathematical functions
– Interpolation, filtering,
smoothing, Fourier analysis
 Extensive plotting capabilities
– 2-D, 3-D, and volume visualization
– T
ools for creating custom plots
Access
72

Expanding the Capabilities of MATLAB
 MathWorks add-on tools for:
– Math, statistics, and optimization
– Control system design and analysis
– Signal processing and communications
– Image processing and computer vision
– Parallel computing and more…
Access
73

Symbolic Math Toolbox
• Perform symbolic math computations.
• Integration & Differentiation
• Simplification, Substitution, and Solving
• Linear Algebra
• Plotting Analytical Function
• Interactive Computations in the MATLAB Live Editor
74

Curve Fitting Toolbox
• Let x = [x1,x2,x3……xn] & y = [y1,y2,y3……yn].
• It means equation of the curve will satisfy to these data points.
• The process of drawing the most approximate curve for a given data points
is called as curve fitting.
75

76
Goodness of Fit (Statistics Parameter Model)
• After fitting data, you should evaluate the goodness of fit.
• Curve Fitting Toolbox™ software supports these goodness-of-fit statistics
for parametric models:
1. The sum of squares due to error (SSE)
2. R-square
3. Adjusted R-square
4. Root mean squared error (RMSE)

77
Statistics & Machine Learning Toolbox
• Cluster Analysis
Unsupervised learning techniques to find natural groupings and patterns in
data
• Regression
Linear, generalized linear, nonlinear, and nonparametric techniques for
supervised learning
• Classification
Supervised learning algorithms for binary and multiclass problems

78
• Dimensionality Reduction and Feature Extraction
PCA, factor analysis, feature selection, feature extraction, and more.
• Box Plots
Compare data distributions.
• Distribution Plots
Visually determine data distributions.

79
• Box Plots
Compare data distributions.

Machine Learning
• Concept: In fig. 1 below
Fig 1 : Concept of Machine Learning

Supervised Learning
• It is a type of machine learning algorithm.
• Each example is a pair of an input data & desire output values.
Fig. 2 Process of Supervised Learning
Input Data
Predefined
Output Data
Learning
Algorithm
Hypothesis
/ Model
Prediction or
Classification

Un-Supervised Learning
• Type of machine learning algorithm.
Fig. 3 Process of Un-Supervised Learning
Input Data
Un-supervised Machine
Learning Algorithm Output

2
Cluster Analysis
Fig 4. Cluster Analysis

85
Fuzzy Logic Toolbox
Fuzzy Logic Toolbox™ provides functions, apps, and a Simulink® block for
analyzing, designing, and simulating systems based on fuzzy logic.

86
Fuzzy Logic Toolbox
The product guides you through the steps of designing fuzzy inference
systems.
Functions are provided for many common methods, including fuzzy clustering
and adaptive neurofuzzy learning.

87
Image Processing Toolbox
1. Color Thresholder
Manipulate color component of the image.
2. Image Acquisition
Specify parameter & acquire image or video.
3. Image Segmentator
Separate Region of Interest (ROI)
3. Region Analyzer
Analyze the segmented region with various parameter.

88
Computer Vision Toolbox
1. Camera Calibrator –
estimate geometric parameter of single camera.
2. Stereo Camera Calibrator –
Estimate geometric parameter of stereo camera.

Signal Processing Toolbox
• Signal Generation and Preprocessing
1. Resampling Signals
2. Signal Smoothing
3. Outlier Removal
4. Detrending
5. Aligning Signals with Different Start Times
6. Signal Generation

• Measurements and Feature Extraction (Time Domain Analysis)
1. Signal Statistics
1. Pulse and Transition Metrics
2. Peak Analysis
3. Envelope Extraction
4. Finding a Signal in a Measurement

Measurements and Feature Extraction (Frequency Domain Analysis)
1. Harmonic Distortion
2. Spurious-Free Dynamic Range (SFDR)
3. Power, Bandwidth and Frequencies
4. Data Reduction and Reconstruction using Walsh-Hadamard Transform.

Digital and Analog Filters
1. Filter Design Gallery
2. FIR Filter Design
3. IIR Filter Design
4. Filter Design and Analysis Tool (FDATool)
5. Filter Visualization Tool (FVTool)
6. Digital Filtering

1
Thank You
Suraj Gawande
Engineer-Technical Support - Mathworks

Thank You
newgen.anand@gmail.com
+91 9443917210

Basic MATLAB-Presentation.pptx

More Related Content

Similar to Basic MATLAB-Presentation.pptx

Recently uploaded

Basic MATLAB-Presentation.pptx

Editor's Notes