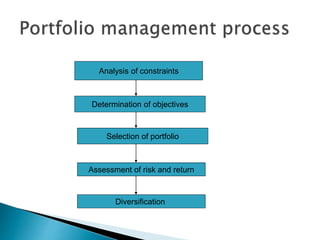
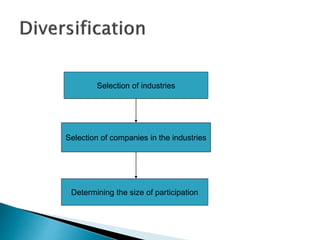
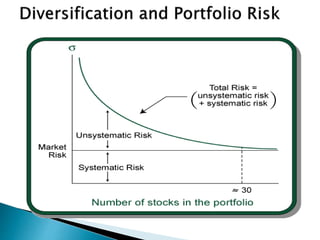
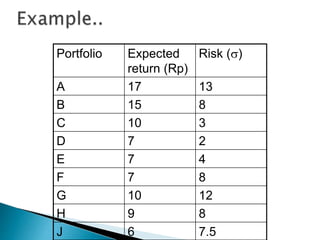
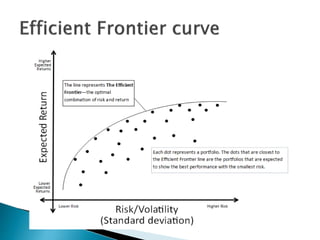
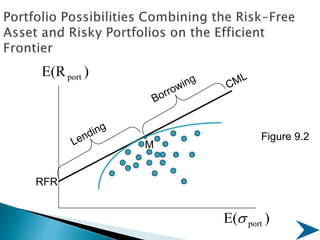
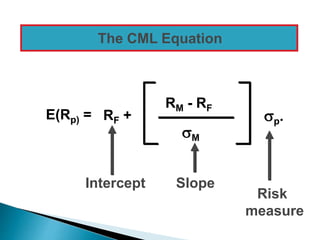
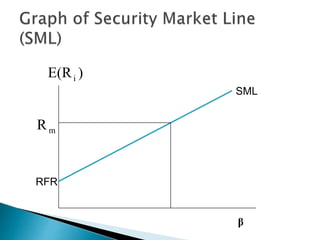
The document discusses portfolio management and the capital asset pricing model (CAPM). It covers key aspects of portfolio construction including diversification, risk and return analysis, and asset selection. It also explains key concepts of the CAPM such as the security market line (SML), capital market line (CML), beta, and the relationship between risk and expected return. The assumptions and limitations of the CAPM are also outlined.

1. The process of blending together the broad
asset classes so as to obtain optimum return
with minimum risk

2. Analysis of constraints
Determination of objectives
Selection of portfolio
Assessment of risk and return
Diversification

3. Selection of industries
Selection of companies in the industries
Determining the size of participation

4.  Portfolio risk can be reduced by
diversification
 The assets may vary from stocks to different
types of bonds
 The portfolio may consist of securities of
different industries
 Different assets are added to the portfolio,
the total risk tends to decrease.

5.  Vast diversification
 Purchase of poor performers
 Information inadequacy
 High research cost

6. Graph:

7. Assumptions
 The individual investor estimates risk on the
basis of variability of returns. Investor’s
decision is solely based on the expected
return and variance of returns only.
 For a given level of risk, investor prefer
higher return to lower return. Likewise, for a
given level of return investors prefers lower
risk than higher risk.

8.  Portfolio expected return: The expected
return on a portfolio is simply the weighted
average of the expected returns on the
individual securities in the portfolio.
 Portfolio risk: It is measured by the variance
or standard deviation and is not the weighted
average of the risks of the individual
securities in the portfolio
 For calculation of portfolio risk we need
information on weighted individual security
risks and weighted comovements between
returns of securities included in the portfolio

9.  A set of optimal portfolios that offers the
highest expected return for a defined level of
risk or the lowest risk for a given level of
expected return.
 Optimal portfolios that comprise the efficient
frontier tend to have a higher degree of
diversification than the sub-optimal ones,
which are typically less diversified.

10. Portfolio Expected
return (Rp)
Risk ()
A 17 13
B 15 8
C 10 3
D 7 2
E 7 4
F 7 8
G 10 12
H 9 8
J 6 7.5

12.  Utility is the satisfaction of the investor from
the portfolio return
 An ordinary investor assumed to receive
greater utility from higher return
 The investor gets more satisfaction or utility
in X+1 than from X rupee.

13.  Risk averse: Rejects a fair gamble because the
disutility of the loss is greater for him than
the utility of gain.
 Risk neutral: He is indifferent to whether a
fair gamble is undertaken or not
 Risk seeking: He would select a fair gamble.
The expected utility of investment is higher
than the expected utility of not investing.

14.  Investor has to consider not only risky assets
but also risk free assets and he should be
able to borrow and lend money at a given
rate of interest is called as leveraged
portfolio.

15.  The assumption of risk-free asset is essential
to the economy.
 The standard deviation of the risk-free asset’s
return is zero because the return is certain.
 The risk-free rate should equal the expected
long run growth rate of the economy with an
adjustment for short-term liquidity.
 The covariance and correlation of the risk-free
asset with any other asset or portfolio will
always equal zero.

16. E(Rp)
p
M
Efficient
Frontier
B
A
Lending
Borrowing
CML
RF

17.  The benefit of diversification arises when the
correlation between the two securities is less
than 1.
 When the securities are perfectly positively
correlated (ρ = 1), the diversification does not
reduce risk.
 When the securities are perfectly negatively
correlated (ρ = -1), diversification results in
maximum risk reduction
 In this case the risk can be reduced to zero,
by choosing the weights suitably.

18. The required rate of return of an asset is
having linear relationship with asset’s
beta(undiversifiable or systematic risk)

19. 1. An individual seller or buyer cannot affect
the price of a stock.
2. Investors can borrow or lend any amount
of money at the risk-free rate of return
3. All investors have homogeneous
expectations; that is, they estimate
identical probability distributions for
future rates of return.
4. All investments are infinitely divisible,
which means that it is possible to buy or
sell fractional shares of any asset or
portfolio.

20. 5. There are no taxes or transaction costs
involved in buying or selling assets.
6. There is no inflation or any change in
interest rates, or inflation is fully
anticipated.
7. Investors make their decisions only on the
basis of the expected returns deviations
and covariance's of all pairs of securities.
8. Unlimited quantum of short sales is
allowed. Any amount of shares an
individual can sell short.

21.  It is assumed that the investor could borrow
or lend any amount of money at risk less
rate of interest.
 When this opportunity is given they can mix
risk free assets with the risky assets in a
portfolio to obtain a desired rate of risk-
return combination.
 The expected return on the combination of
risky and risk free combination is

22.  When a risk-free asset is added to the
feasible set, investors can create portfolios
that combine this asset with a portfolio of
risky assets.
 The straight line connecting RF with M, the
tangency point between the line and the
old efficient set, becomes the new efficient
frontier.
What impact does RF have on
the efficient frontier?

23. )
E( port

)
E(Rport
Figure 9.2
RFR
M

24.  The Capital Market Line (CML) is all linear
combinations of the risk-free asset and
Portfolio M.
 Portfolios below the CML are inferior.
◦ The CML defines the new efficient set.
◦ All investors will choose a portfolio on the CML.
What is the Capital Market Line?

25. E(Rp) = RF +
Slope
Intercept
p.
The CML Equation
RM - RF
M
Risk
measure

26.  The expected rate of return on any
efficient portfolio is equal to the risk-free
rate plus a risk premium.
 The optimal portfolio for any investor is
the point of tangency between the CML
and the investor’s indifference curves.
What does the CML tell us?

27.  The CML gives the risk/return relationship
for efficient portfolios.
 The Security Market Line (SML), also part of
the CAPM, gives the risk/return relationship
for individual stocks.
What is the Security Market Line (SML)?

28.  The measure of risk used in the SML is the
beta coefficient of company.
 The SML equation:
Ri = RF + (RM-Rf) βi
The SML Equation

29. )
E(Ri
RFR
m
R
SML
β

30. Compare the required rate of return to the
expected rate of return for a specific risky
asset using the SML over a specific
investment horizon to determine if it is an
appropriate investment
Independent estimates of return for the
securities provide price and dividend
outlooks

31.  The CAPM focuses on the market risk,
makes the investors to think about riskiness
of the assets
 The CAPM has been useful in the selection
of securities and portfolios
 In the CAPM one can find out the expected
returns for a firm’s security
 It is a useful tool for financial analysis
 The inputs of CAPM keeps changing, so
CAPM model is also subject to criticism

32.  Based on the law of one price. Two items
that are the same cannot sell at different
prices
 If they sell at a different price, arbitrage will
take place in which arbitrageurs buy the good
which is cheap and sell the one which is
higher priced till all prices for the goods are
equal

33.  The investors have homogenous expectations
 The investors are risk averse and utility
maximizers
 Perfect competition prevails in the market
and there is no transaction cost.

34.  In APT, the assumption of investors utilizing
a mean-variance framework is replaced by
an assumption of the process of generating
security returns.
 APT requires that the returns on any stock
be linearly related to a set of indices.
 In APT, multiple factors have an impact on
the returns of an asset in contrast with
CAPM model that suggests that return is
related to only one factor, i.e., systematic
risk

35.  While all assets may be affected by growth
in GNP, the impact will differ.
 Which firms will be affected more by the
growth in GNP?
 The APT assumes that, in equilibrium, the
return on a zero-investment, zero-
systematic risk portfolio is zero, when the
unique effects are diversified away:
 E(ri) = 0 + 1bi1 + 2bi2 + … + kbik