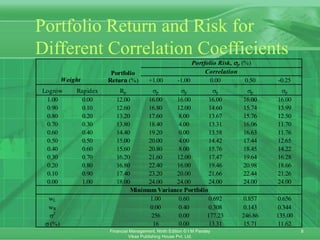
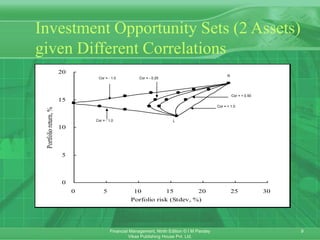
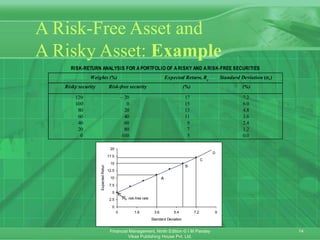
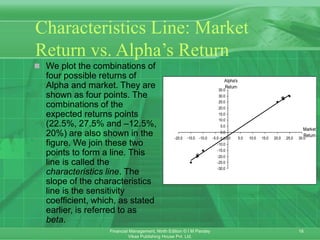
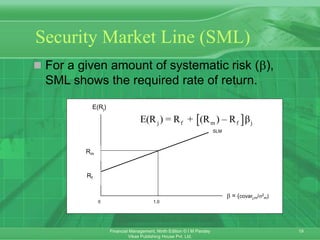
This chapter discusses portfolio theory and asset pricing models. It introduces concepts such as portfolio risk and return, systematic and unsystematic risk, the efficient frontier, and the capital asset pricing model (CAPM). CAPM holds that the expected return of an asset is determined by its sensitivity to non-diversifiable market risk (beta) and the expected market return. The chapter also covers the arbitrage pricing theory, which attributes an asset's return to multiple systematic factors rather than just one market factor.