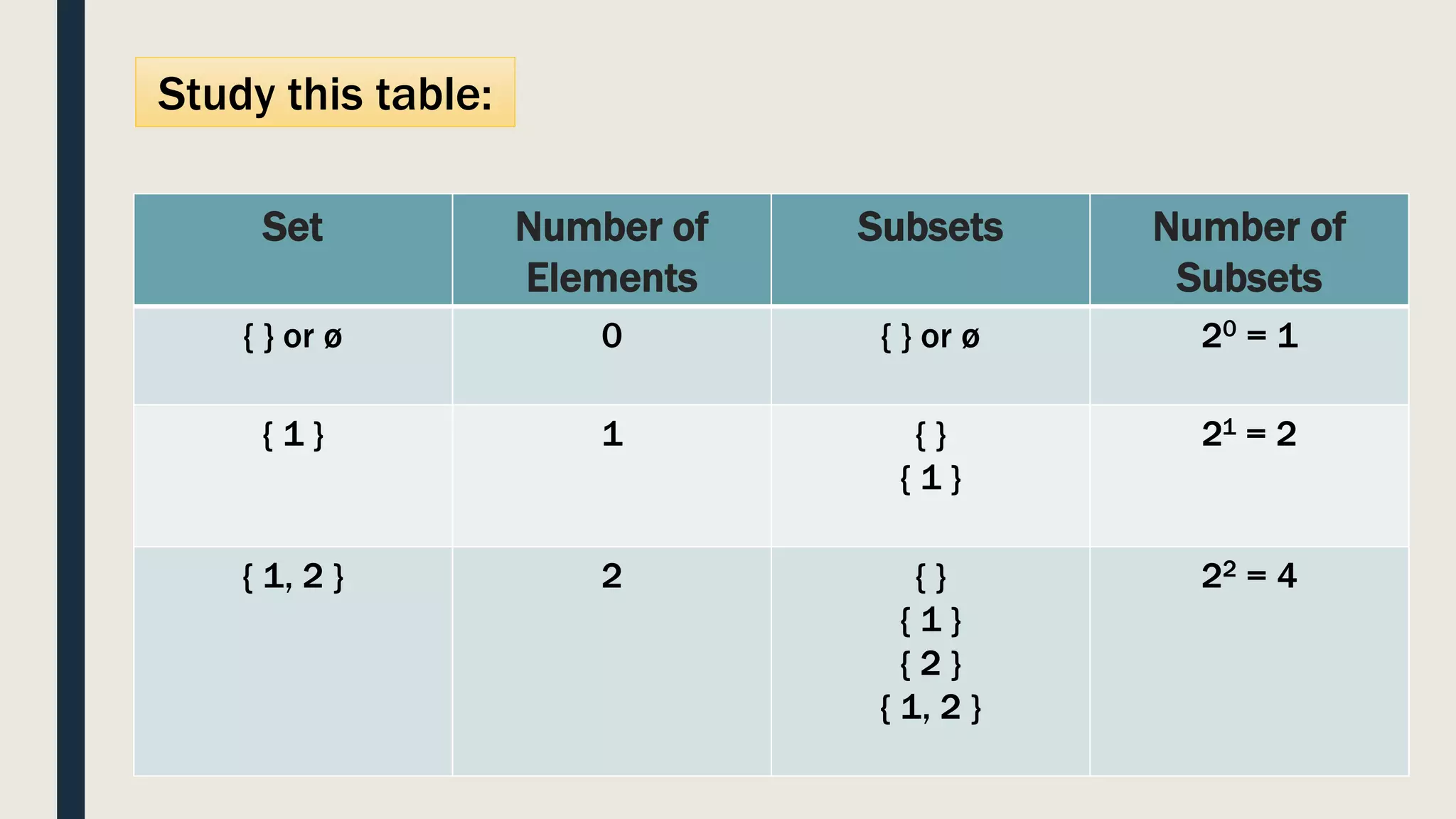
A subset is a set that contains elements of another set. A proper subset contains some but not all elements of the original set. There are symbols to denote different subset relationships: ⊂ for proper subset, ⊆ for subset, ⊃ for proper superset, and ⊇ for superset. The number of subsets of a set with n elements is 2n. The empty set is a subset of all sets, and every set is a subset of itself.

2. Subsets
A subset is made up of components of another set. If every member of Set A
is also a member of Set B, then Set A is said to be a subset B and denoted by A
⊆ B meaning, “ A is contained in B”. If A is a subset of B, but not equal to B, then
A is a proper subset of B which is denoted by A ⊂ B.
Proper subset is a subset which is not the same as the original set itself.
The following symbols are used for subsets.
⊂ - “is a proper subset of”
⊃ - “is a proper superset of”
⊆ - “is a subset of”
⊇ - “is a superset”
⊄ - “is not a subset of”

3. Proper subset and proper superset relationship.
■ The symbol ⊂ is used to denote proper subset and its inverse ⊃ is
used to denote proper superset relationship.
■ Examples:
1. Let A = {1, 2, 3 } and B = {1, 2, 3, 4, 5}
thus, A ⊂ B and B ⊃ A
2. Let C = { 2, 4, 6, 8, 10} and D = {x / x is a counting number less than 15}
then, C ⊂ D and D ⊃ C

4. Subset and superset relationship
■ The symbol ⊆ is used to denote subset and its inverse ⊇ is used
to denote a superset relationship.
■ Examples:
1. Let M = {1, 3, 5, 7, 9} and N = {1, 3, 5, 7, 9}
then, M ⊆ N and N ⊇ M
2. Let R = { 2, 4, 6, 8 10 } and S = {x / x is the first five even number}
then, R ⊆ S and S ⊇ R

5. Let’s Learn More!
Let G = {0, 2, 4, 6, 8, 10}
H = {2, 6, 10}
I = {2, 5, 8, 10}
J = {6, 10, 2}
A = is an empty set
The following statements are true.
1. H ⊂ G because every element of H is also an element of G.
2. I ⊄ G (read as I is not a subset of G) because one element of I,
which is 5 is not an element of G.
3. J ⊆ H because every element of J is also an element of H.

6. The empty set is always a subset of any set.
So, we write ø ⊂ A or { } ⊂ A.
Moreover, every set is a subset of itself. We write A ⊆ A.
Example:
Let A = { 2, 4}. Can you list all the subsets of A?
The null set / empty set is a subset of A.
A is a subset of itself.
The other subsets of A are {2} and {4}
So, the subsets of A are { }, {2}, {4}, and {2, 4}. There are 4 subsets of A.

7. Study this table:
Set Number of
Elements
Subsets Number of
Subsets
{ } or ø 0 { } or ø 20 = 1
{ 1 } 1 { }
{ 1 }
21 = 2
{ 1, 2 } 2 { }
{ 1 }
{ 2 }
{ 1, 2 }
22 = 4

8. { 1, 2, 3 } 3 { }
{ 1 }
{ 2 }
{ 3 }
{ 1, 2 }
{ 1, 3 }
{ 2, 3 }
{ 1, 2, 3 }
23 = 8
If A has n elements, then it has 2n subsets.

9. Thank You!