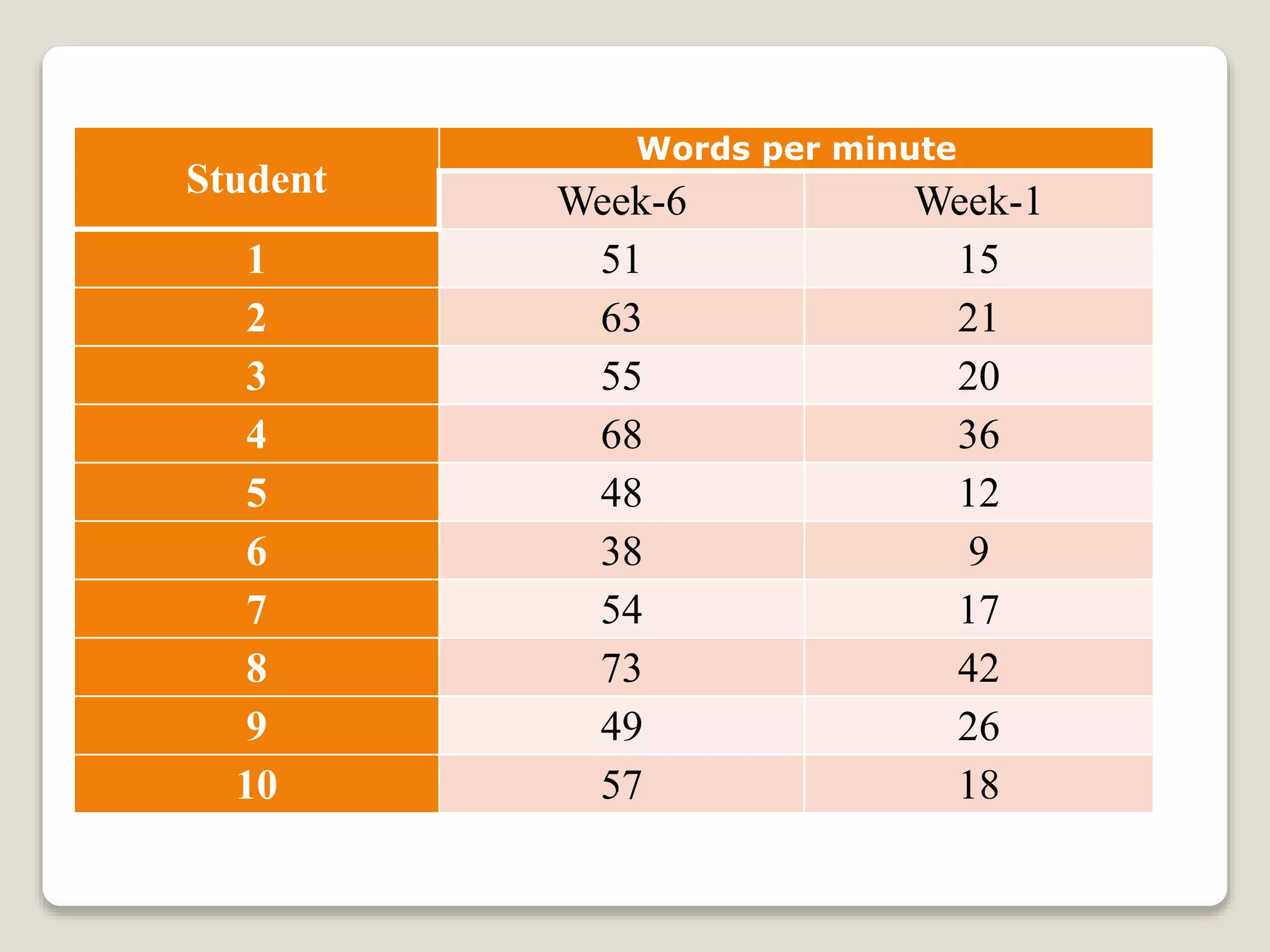
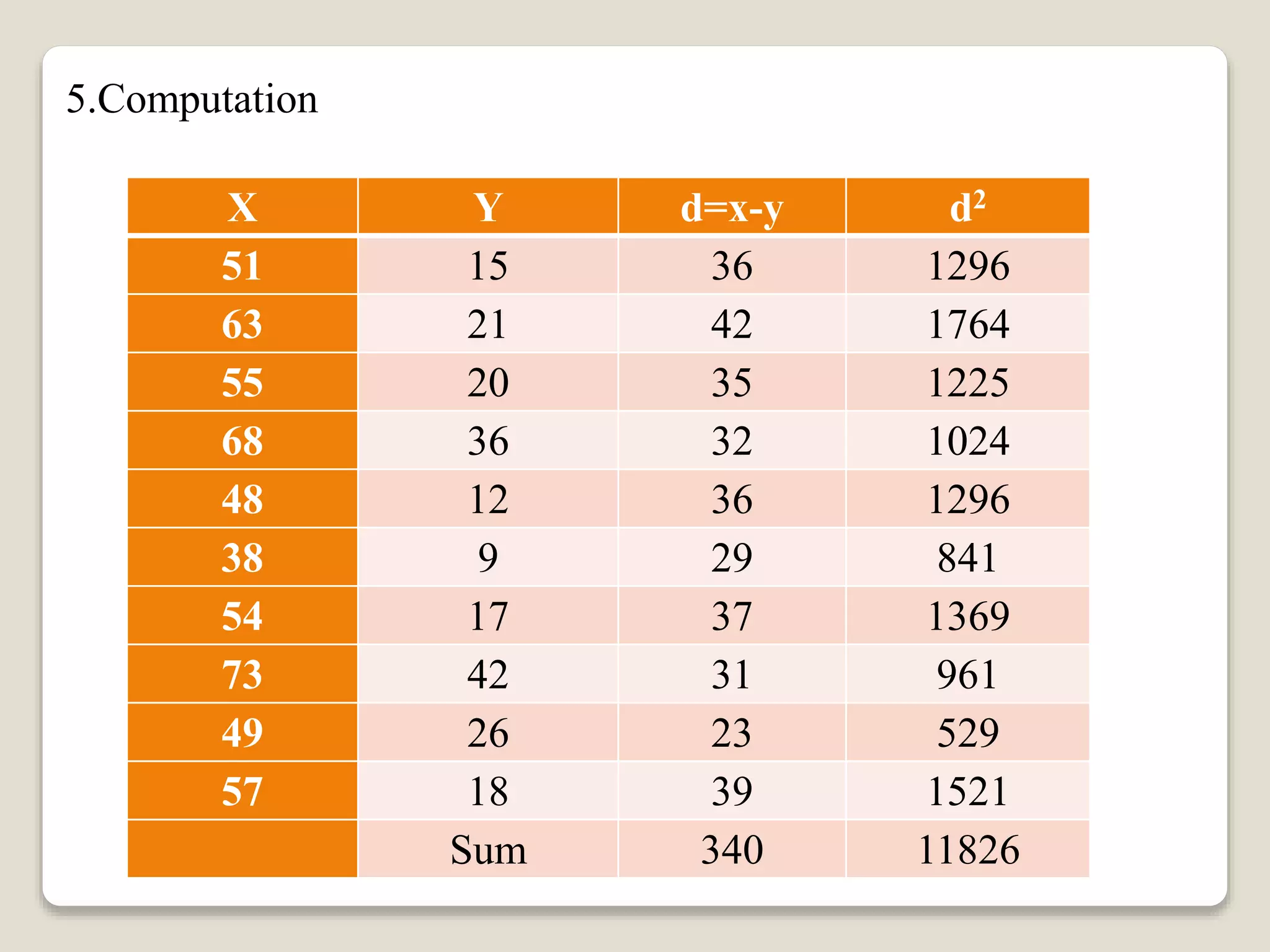
This document discusses paired t-tests and provides an example problem. It introduces paired t-tests as a statistical test used to compare the means of two related groups or measurements on the same item to determine if there is a significant difference. The example problem tests the hypothesis that students' average typing speed increased by over 30 words per minute after completing a typing course, using a paired t-test with a sample of 10 students' pre-and post-course typing speeds. The calculated t value is compared to the critical value to determine whether to reject the null hypothesis.

1. HYPOTHESIS TESTING
PART-IV
PAIRED OBSERVATIONS
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Paired t-test
A paired t-test is a statistical test that compares the means of two
related groups to determine if there is a significant difference
between the two groups or if you have two measurements on the
same item, person or thing. Paired t-test is also known as a
dependent or correlated t-test.
Example-1
In-charge of an institute wants to measure the increase in typing
speed for students. Typing tests were taken at the end of the first
week and at the end of the course (4th week).
Example-2
Weights of children before and after a feeding.
Example-3
10 students were placed on a special diet, The result weight before
diet and after diet.

3. Test Concerning paired mean
Example-3
The Director of an institute wants to measure the
increase in typing speed for students who have
completed their course. She selected a random sample
of 10 students. Typing tests were taken at the end of
the first week and at the end of the course(sixth week).
Test the hypothesis that the average student will
increase in typing speed by over 30 words per minute
between weeks one and six. Use α = 0.05.

4. Student
Words per minute
Week-6 Week-1
1 51 15
2 63 21
3 55 20
4 68 36
5 48 12
6 38 9
7 54 17
8 73 42
9 49 26
10 57 18

5. 1.Hypothesis H0: 𝜇 𝐷 = 30
H1: 𝜇 𝐷 ˃ 30
2.Level of significance α = 0.05
3.Test statistic
4.Critical Region
In case of upper tail test i.e. H1 𝑖𝑠 ˃.
Reject H0, if 𝑡 𝑐𝑎𝑙 ≥ 𝑡𝑡𝑎𝑏
Where 𝑡𝑡𝑎𝑏 = 𝑡 𝛼 , 𝑛−1 = 𝑡0.05, 10−1 = 𝑡0.05,9=1.833
𝑡 𝑐𝑎𝑙 ≥ 1.833
D
d
d
t
s
n


 –0– 1.833
Solution:

6. X Y d=x-y d2
51 15 36 1296
63 21 42 1764
55 20 35 1225
68 36 32 1024
48 12 36 1296
38 9 29 841
54 17 37 1369
73 42 31 961
49 26 23 529
57 18 39 1521
Sum 340 11826
5.Computation

7.  
 
2 2
1
n d d
sd
n n
 


 2
10(11826) 340
5.44
10(10 1)
sd

 

34 30
5.44
10
2.33
t
t
cal



6.Conclusion: Reject H0.