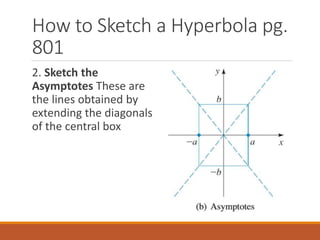
This document discusses hyperbolas and how to sketch them. It defines a hyperbola as the set of points where the difference between the distances to two fixed foci is a constant. It provides the equations of horizontal and vertical hyperbolas with their vertices, asymptotes, and foci. Finally, it outlines the four steps to sketch a hyperbola: 1) sketch the central box, 2) draw the asymptotes, 3) plot the vertices, and 4) sketch each branch approaching the asymptotes.

1. 11.3 Hyperbolas
pg. 799

2. Geometric Definition of a
Hyperbola pg. 799
A hyperbola is the set of
all points in the plane,
the difference of whose
distances from two fixed
points 𝐹1 and 𝐹2 is a
constant. These two
fixed points are the foci
of the hyperbola

3. Hyperbola with center at the
Origin pg. 800 (horizontal)
Equation
𝑥2
𝑎2 −
𝑦2
𝑏2 = 1 𝑎 > 0, 𝑏 > 0
Vertices
(±𝑎, 0)
Transverse Axis
Horizontal, length 2𝑎
Asymptotes
𝑦 = ±
𝑏
𝑎
𝑥
Foci
±𝑐, 0 , 𝑐2 = 𝑎2 + 𝑏2

4. Hyperbola with center at the
Origin pg. 800 (vertical)
Equation
𝑦2
𝑎2 −
𝑥2
𝑏2 = 1 𝑎 > 0, 𝑏 > 0
Vertices
(0, ±𝑎)
Transverse Axis
Vertical, length 2𝑎
Asymptotes
𝑦 = ±
𝑎
𝑏
𝑥
Foci
0, ±𝑐 , 𝑐2 = 𝑎2 + 𝑏2

5. How to Sketch a Hyperbola pg.
801
1. Sketch the Central
Box This is the rectangle
centered at the origin,
with sides parallel to the
axis, that crosses one
axis at ±𝑎 and the other
at ±𝑏

6. How to Sketch a Hyperbola pg.
801
2. Sketch the
Asymptotes These are
the lines obtained by
extending the diagonals
of the central box

7. How to Sketch a Hyperbola pg.
801
3. Plot the Vertices
These are the two 𝑥-
intercepts or the two 𝑦-
intercepts
4. Sketch the Hyperbola
Start at the vertex, and
sketch a branch of the
hyperbola, approaching
the asymptotes. Sketch
the other branch in the
same way