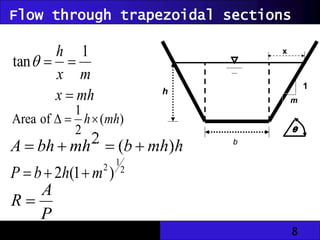
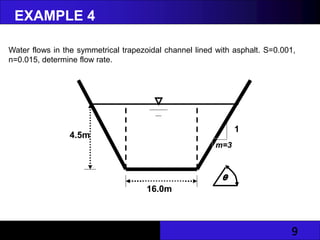
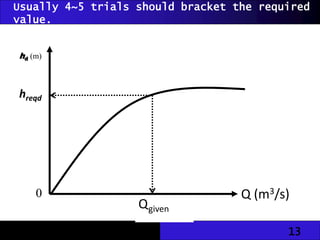
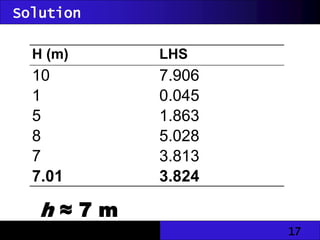
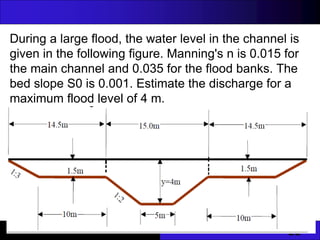
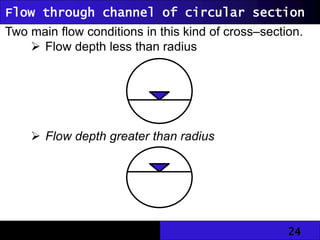
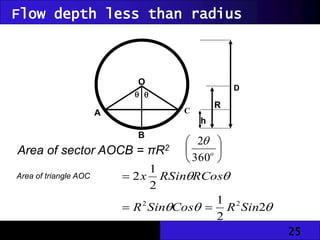
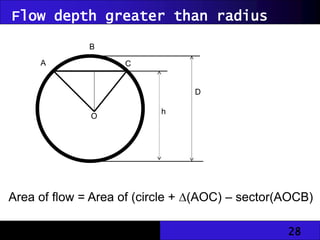
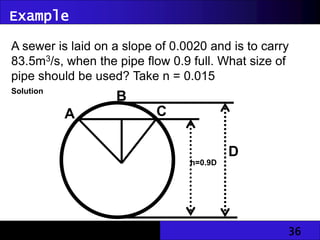
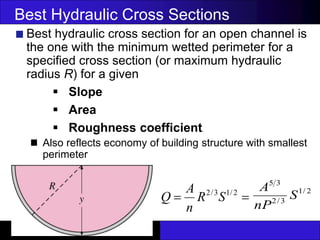
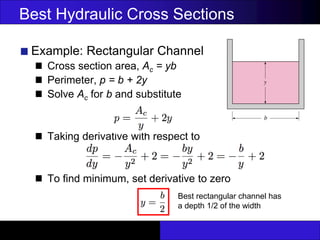
The document discusses hydraulic engineering concepts related to open channel flow, including turbulent and laminar flow characteristics, freeboard design, and methods for calculating flow rates based on given dimensions and parameters. It details various design problems encountered in open channels, provides examples, and covers calculations for different channel shapes such as rectangular, trapezoidal, and circular. Various formulas, including Manning's equation, are presented to determine flow characteristics in different scenarios.

1. CE 356
HYDRAULIC ENGINEERING
Dr. Kwaku Amaning Adjei
Department of Civil Engineering
KNUST
Kumasi

2. 2
Open Channel Uniform Flow Formulas
 Flow in most channels is turbulent.
 Laminar flow in open channels is very rare.
b
c
t
T
D
h
θ
Free board
T=Top width of the channel; t=width of water surface for depth h; h= flow
depth in channel; D=Depth of channel after free board is added; b=bottom
width; c=length of wetted sides of channel; θ= angle b/n sloping side and the
horizontal

3. 3
Freeboard
 The vertical distance from the top of the channel
(retaining banks) to the water surface (highest
anticipated) at the design condition.
 It should be sufficient to prevent waves or
fluctuation in the water surface from overflowing
the sides.
 No universal rule for the determination of the
freeboard.
 However, freeboards varying from 5% to 30% of
the depth of flow are commonly used in design.

4. 4
Some recommended values for freeboard
Channel flow
rate (m3/s)
2~10 1~2 0.5~1.0 <0.5
Recommended
freeboard (m)
0.4~0.6 0.35 0.25 0.15

5. 5
Hydraulic Design of Open Channels
There are two main types of design
problems encountered in open channel flow
studies.
Given the depth, determine flow rate
Given the flow rate, determine depth

6. 6
Flow through rectangular sections
h
b
h
h
b
P
2





b
h
hb
A 
h
b
bh
P
A
R
2




7. 7
Water flows in a rectangular concrete open channel of slope 0.0028, bed width
12.0m, and flow depth 2.5m. If n=0.013, determine flow velocity and flow rate.
m
P
A
R 765
.
1
5
.
2
0
.
12
5
.
2
0
.
12
5
.
2






2
/
1
3
/
2
1
S
R
n
v  s
m/
945
.
5
013
.
0
)
0028
.
0
(
)
765
.
1
(
1 2
/
1
3
/
2



s
VA
Q /
3
m
178
945
.
5
12
5
.
2 




Solution
Given S = 0.0028, n=0.013
EXAMPLE 3
12.0 m
2.5
m

8. 8
h
mh
b
mh
bh
A )
(
2 



2
1
2
)
1
(
2 m
h
b
P 


θ
h
b
m
1
m
x
h 1
tan 


mh
x 
)
(
2
1
of
Area mh
h


Flow through trapezoidal sections
P
A
R 
x

9. 9
EXAMPLE 4
Water flows in the symmetrical trapezoidal channel lined with asphalt. S=0.001,
n=0.015, determine flow rate.
θ
4.5m
16.0m
m=3
1

10. 10
Solution 4
Given S = 0.001, n = 0.015, m = 3
h
mh
b
mh
bh
A )
(
2 



2
1
2
)
1
(
2 m
h
b
P 


A= (16 + 3 x 4.5) x 4.5 = 132.75 m2,
P = 44.46 m
m
987
.
2


P
A
R

11. 11
s
m
S
R
n
A
AV
Q
/
297
.
580
015
.
0
)
001
.
0
(
)
987
.
2
(
8
.
132
3
2
/
1
3
/
2
2
/
1
3
/
2






Solution 4

12. 12
Graphical Method
Assume values of h and calculate A, P, R and then
Q.
The two values of h that bracket the given Q should
also bracket the value of hrequired
h (m) A (m2) P (m) R (m) Q (m3/s)
h1 A1 P1 R1 Q1
h2 A2 P2 R2 Q2
‘ ‘ ‘ ‘ ‘
‘ ‘ ‘ ‘ ‘
hn An Pn Rn Qn

13. 13
Usually 4~5 trials should bracket the required
value.
0
hreqd
hd (m)
Q (m3/s)
Qgiven

14. 14
Determine the height required for a rectangular
channel 20m wide laid on a slope of 0.0001 transport
water at the rate of 240 m3/s? Take n = 0.015.
Example 5
Solution
Employing the Manning's Formula
2
1
3
2
1
S
AR
n
Q 
h
P
h
A
2
20
20




15. 15
  2
1
3
2
0001
.
0
2
20
20
20
240 







h
h
n
h
 
01
.
0
2
20
20
12
3
2








h
h
n
h
3
2
2
20
20
015
.
0
1200 







h
h
h
Solution

16. 16
3
2
2
20
20
18 







h
h
h
h
h
h
h
h
h
h
2
20
818
.
3
2
20
20
37
.
76
2
20
20
18
2
5
2
5
2
3
2
3












Solution

17. 17
H (m) LHS
10 7.906
1 0.045
5 1.863
8 5.028
7 3.813
7.01 3.824
h ≈ 7 m
Solution

18. 18
How wide must a rectangular channel be constructed
in order to carry 500m3/s of water at a depth of 6m on
a slope of 0.0004 and n = 0.010?.
Example 6
Solution
Employing the Manning's Formula
b
h
b
P
b
bh
A






12
2
6
b
b
R


12
6

19. 19
2
1
3
2
S
R
n
A
Q 
 
























b
b
b
b
b
b
b
b
b
12
6
957
.
268
12
6
667
.
41
0004
.
0
12
6
01
.
0
6
500
2
3
3
2
2
1
3
2
Solution 6

20. 20
b
b


12
82
.
44
2
5
Assumed b LHS
10 14.37
20 55.9
15 32.27
18 45.82
17 41.08
17.8 44.857
b ≈ 17.8 m
Solution 6

21. 21
Flow through Compound Channels
A compound channel may be defined as a
channel in which various sub areas have
different flow properties.
 Surface roughness, n,
 Flow area, A.
 A natural river/stream having over bank (flood plain)
flow during a flood is a typical example of a
compound channel.
In analyzing flow through a compound channel
the conveyance (K) is found to be of great help.

22. 22
During a large flood, the water level in the channel is
given in the following figure. Manning's n is 0.015 for
the main channel and 0.035 for the flood banks. The
bed slope S0 is 0.001. Estimate the discharge for a
maximum flood level of 4 m.

23. 23
Solution
Split the section into subsections (1), (2) and
(3) and apply Manning’s equation to each
one in turn and then sum the discharges.

24. 24
Flow through channel of circular section
Two main flow conditions in this kind of cross–section.
 Flow depth less than radius
 Flow depth greater than radius

25. 25
Flow depth less than radius
h
R
D
C
O
B
A

Area of sector AOCB = πR2

C






o
360
2
Area of triangle AOC





2
2
1
2
1
2
2
2
Sin
R
Cos
Sin
R
RCos
RSin
x




26. 26
Area of flow = Area of sector – Area of
triangle


 2
2
1
360
2 2
0
2
Sin
R
R
A 







The perimeter






 0
360
2
2

R
P

27. 27
The hydraulic radius















0
2
0
2
360
2
2
2
2
1
360
2





R
Sin
R
R
P
A
Rh














0
45
2
90




 RSin
R
S
R
n
A
Q h
3
2


28. 28
Flow depth greater than radius
A
B
h
D
C
Area of flow = Area of (circle + (AOC) – sector(AOCB)
O

29. 29








 o
R
Sin
R
R
360
2
2
2
1
flow
of
Area 2
2
2 



Perimeter = Perimeter of (circle – sector)
= 2R - 2R 





o
360
2







 0
90
2

R

















0
0
2
2
2
90
2
360
2
2
2
1






R
R
Sin
R
R
P
A
Rh

30. 30
































0
0
0
45
4
90
2
2
90
2
2
360
2
2
2
2












R
RSin
R
R
RSin
R
Rh
S
R
n
A
Q h
3
2


31. 31
EXAMPLE
A circular sewer 1m in diameter conveys a discharge
of water at a depth of 0.2m. If the sewer is laid at a
slope of 1 in 500 find the rate of flow. Take C= 60
C
O
B
A

0.2 m

32. 32
Solution
0
1
1
13
.
53
5
.
0
3
.
0













 
 

Cos
R
h
R
Cos

Area of flow = 

 2
2
1
180
2
0
2
Sin
R
R 






= 0.2319 – 0.12 = 0.1119m2
Perimeter of flow = 





0
360
2
2

R
= 0.928m

33. 33
Hydraulic radius Rh = m
P
A
1206
.
0
928
.
0
1119
.
0


500
1206
.
0
1119
.
0
60 


 S
R
CA
Q h
= 0.1124m3/s

34. 34
Example
The depth of water in a circular brick lined conduit
1.8m in diameter is to be 1.5m and the flow rate
2.16 x 105 m3/day. Find the gradient of the conduit.
Take C = 67.
Solution
0
1
1
19
.
48
9
.
0
6
.
0







 
 

Cos
R
R
h
Cos

Area of flow = 






 0
2
2
2
180
2
2
1 


 R
Sin
R
R
= 2.5457 + 0.4025 – 0.6735
= 2.2747m2

35. 35
Perimeter P 






 0
180
1
2

R = 4.133m
Hydraulic Radius Rh =
133
.
4
2747
.
2
= 0.55m
From Q = RS
AC
2042
1
10
8964
.
4
55
.
0
4489
17
.
5
25
.
6
4
2
2
2








R
C
A
Q
S

36. 36
Example
A sewer is laid on a slope of 0.0020 and is to carry
83.5m3/s, when the pipe flow 0.9 full. What size of
pipe should be used? Take n = 0.015
Solution
A
B
h=0.9D
D
C

37. 37
Area of flow = 






 0
2
2
2
360
2
2
2
1 


 R
Sin
R
R
2
D
R 
2
2
2
2
0
2
0
2
2
2
7448
.
0
12
.
0
6248
.
0
2
8
180
1
4
720
2
8
4
D
D
D
Sin
D
D
D
Sin
D
D
A




























0
1
1
87
.
36
5
.
0
4
.
0
5
.
0
5
.
0
9
.
0













 
 

Cos
D
D
D
Cos


38. 38
Perimeter,
D
D
R
P
50
.
2
180
1
180
2
0
0





















D
D
D
P
A
Rh 298
0
50
2
7448
0 2
.
.
.



     
53
.
266
3323
.
0
565
.
88
0002
.
0
298
.
0
7448
.
0
015
.
0
1
5
.
83
3
8
3
8
2
1
3
2
2
3
2




D
D
D
x
D
x
S
R
n
A
Q

39. 39
D D8/3
8 256
9 350.466
8.5 300.92
8.2 273.42
8.1 264.62
m
1
.
8

D

40. 40
Exercise: A 50cm diameter concrete pipe on a slope of
0.002 is to be used for conveying water of a flow rate of
0.04m3/s. If n=0.013, determine the flow depth.
Example

41. Best Hydraulic Cross Sections
Best hydraulic cross section for an open channel is
the one with the minimum wetted perimeter for a
specified cross section (or maximum hydraulic
radius R) for a given
 Slope
 Area
 Roughness coefficient.
Also reflects economy of building structure with smallest
perimeter

 2
/
1
3
/
2
S
R
n
A
Q
2
/
1
3
/
2
3
5
S
nP
A

42. Best Hydraulic Cross Sections
Example: Rectangular Channel
Cross section area, Ac = yb
Perimeter, p = b + 2y
Solve Ac for b and substitute
Taking derivative with respect to
To find minimum, set derivative to zero
Best rectangular channel has
a depth 1/2 of the width

43. 43
For a trapezoidal section the area of flow is given as
2
mh
bh
A 

mh
h
A
b 


)
1
(
2 2
m
h
b
P 


  )
(
1
2 2
h
f
m
h
mh
h
A
P 




Q will be largest when the perimeter is smallest









 2
1
2 m
h
mh
h
A
dh
d
dh
dP

44. 44
2
2
1
2 m
m
h
A
dh
dP





Substitute  h
mh
b
A 
 into
dh
dP
2
2
2
1
2 m
m
h
mh
bh
dh
dP










 


2
1
2
2 m
m
h
b






45. 45
For minimum value,
0

dh
dP
 
m
m
h
b


 2
1
2
- Best hydraulic section ratio of
width to depth
best
h
b



46. 46
  )
(
1
2 2
m
f
m
m
h
b
best
best








m.
only
of
Function
m 0 0.25 0.5 0.75 1.00 1.25 1.50 1.75 2.00 2.50 3.00
2 1.56 1.24 1.00 0.83 0.70 0.61 0.53 0.47 0.39 0.32
best

e.g. for m=0, rectangular cross section
best
 = 2 =
h
b
 b = 2h

47. 47
Question
Which channel is the best ? (with the
same n, So)