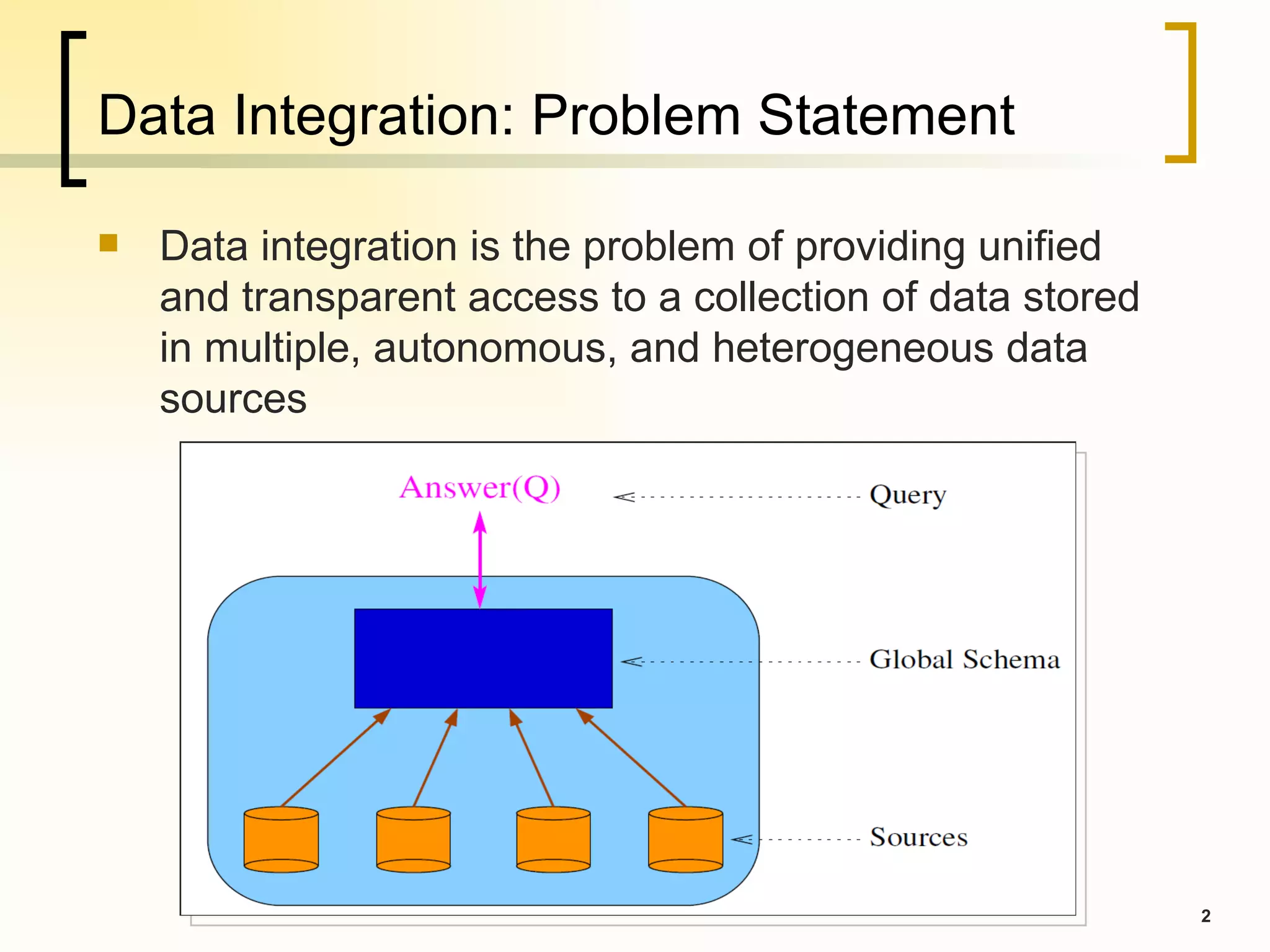
Data integration involves providing unified access to data stored across multiple heterogeneous data sources. There are several data integration architectures including data warehouses, virtual mediators, and peer-to-peer integration. Key challenges in data integration include modeling the global schema, source schemas, and mappings between them, as well as reformulating queries over the global schema to retrieve answers from the source schemas. Languages for modeling schema mappings include GAV, LAV, and GLAV, with different advantages for query reformulation and modularity when new sources are added.

1. Data Integration Techniques and Languages Validation of Mappings

2. Data Integration: Problem Statement Data integration is the problem of providing unified and transparent access to a collection of data stored in multiple, autonomous, and heterogeneous data sources

3. Integration Architectures Distributed databases Data sources are homogeneous databases under the control of the distributed database management system. Multidatabase or federated databases Data sources are autonomous, heterogeneous databases. (Mediator-based) data integration Access through a global schema mapped to autonomous and heterogeneous data sources. Two approaches: Virtual Mediator Data Warehouse Peer-to-peer data integration Network of autonomous systems mapped one to each other, without a global schema.

4. Data Warehouse Architecture Data source Data source Data source (Relational?) database (warehouse) User queries OLAP / Decision support/ Data mining Extract, Transform, Load (ETL)

5. (Virtual) Mediator Architecture Data source wrapper Data source wrapper Data source wrapper Sources can be: relational, hierarchical (IMS), structured files, web sites. Mediator: User queries Mediated schema Data source catalog Reformulator Optimizer Execution engine

6. Warehousing Vs. Virtual Advantages of warehousing: Typically more efficient No need to touch sources at query time Query processing is “traditional” Advantages of Virtual: Up-to-date data Easier to set up (can do it incrementally) Applicable in broader contexts

7. P2P Data Integration Architecture Q Q1 Q3 Q2

8. Main problems in data integration How to construct the global schema. How to discover mappings between sources and global schema. Data extraction, cleaning, and reconciliation. How to process updates expressed on the global schema and/or the sources How to model the global schema, the sources, and the mappings between the two. How to answer queries expressed on the global schema. How to optimize query answering.

9. The Data Integration Modeling Problem How to model the global schema: data model constraints How to model the sources: data model (conceptual and logical level) access limitations data values (common vs. different domains) How to model the mapping between global schemas and sources. How to verify the quality of the modeling process.

10. The Query Reformulation Problem Given: A query Q posed over the mediated schema Descriptions of the data sources Find: A query Q’ over the data source relations, such that: Q’ provides only correct answers to Q, and Q’ provides all possible answers from to Q given the sources. This process heavily depends on the approach adopted for modeling the data integration system.

11. Languages for Schema Mapping Modeling Mediated Schema Source Source Source Source Source GAV Q Q’ Q’ Q’ Q’ Q’ LAV GLAV

12. Global-as-View (GAV) Mediated schema defined as a set of views over the data sources S1 Movie (MID, title ) MovieDetails (MID, director , genre , year ) S2 MovieGenres ( title , genre ) S3 MovieDirectors ( title , dir ) S4 MovieYears ( title , year ) Movie(title,director,year,genre)  S2.MovieGenres(title,genre), S3.MovieDirectors(title,director), S4.MovieYears(title,year) Movie(title,director,year,genre)  S1.Movie(MID,title), S1.MovieDetais(MID,director, genre,year) Movie: title, director, year, genre

13. GAV: Formalization A set of expressions of the form: or G i : relation in mediated schema : query over source relations closed-world assumption open-world assumption

14. Local-as-View (LAV) Data sources defined as views over mediated schema S5 MovieGenres ( title , genre ) S6 ActorDirectors ( actor , director ) S5.MovieGenres(title, genre)  Movie(title, director, year, genre) S6.ActorDirectors(actor, director)  Movie(title, director, year, genre), Actors(title, actor), year ≥ 1980 Movie: title, director, year, genre Actors: title, name

15. LAV: Formalization A set of expressions of the form: or S i : source relation : query over mediated schema closed-world assumption open-world assumption

16. GAV vs LAV Not modular Addition of new sources changes the schema mapping Can be awkward to write mediated schema without loss of information Query reformulation easy Often reduces to view unfolding (polynomial) Can build hierarchies of mediated schemas Best when Few, stable, data sources well-known to the mediator (e.g. corporate integration) Modular--adding new sources is easy Very flexible--power of the entire query language available to describe sources Reformulation is hard Involves answering queries only using views (can be intractable) Best when Many, relatively unknown data sources possibility of addition/deletion of sources

17. Query Reformulation in GAV: Example Source Schemas: S1: {Movie(MID,title), MovieDetails(MID, director, genre, year)} S2: {Cinemas(location, movie, startTime)} Mediated Schema: Movie(title, director, genre, year)  S1.Movie(MID,title), S1.MovieDetails(MID, director, genre, year) Plays(movie, location, startTime)  S2.Cinemas(location, movie, startTime) Query over mediated Schema: Q(title, location, startTime)  Movie(title, x, ‘comedy’, y), Plays(title, location, startTime), starTime > 20h F 1 F 2

18. Query Reformulation in GAV: Example (cont.) Q(t, l, s)  Movie(t, x, ‘comedy’, y), Plays(t, l, s), s > 20h Q(t, l, s)  S1.Movie(MID, t), S1.MovieDetails(MID, x, ‘comedy’, y) , Plays(t, l, s), s > 20h Q(t, l, s)  S1.Movie(MID, t), S1.MovieDetails(MID, x, ‘comedy’, y), S2.Cinemas(l, t, s) , s > 20h unfolding F 1 unfolding F 2

19. Query Reformulation in LAV: Example Movie(MID, title,year,genre) Director(MID, director) Actor(MID, actor) Mediated Schema S1.Comedies(m,t,y)  …… Movie(m, t, y, ‘comedy’), …… y ≥ 1950 S2.Diractors(m,d)  ……. Director(m, d), Actor(m, d) Q(t,y,d)  Movie(m,t,y, ‘comedy’), y ≥ 1950, Director(m,d), Actor(m,d) Q’(t,y,d)  S1.Comedies(m,t,y), S2.Diractors(m,d) Answering Queries Using Views Algorithm

20. Answering Queries Using Views (AQUV) Given: Query Q View definitions: V 1 ,…,V n Find : A query Q’ that is a rewriting of Q that refers only to the view and interpreted predicates Def. Q’ is an equivalent rewriting of Q using V 1 ,…,V n if Q’  Q , i.e. Q’ ⊑ Q and Q’ ⊒ Q When Q, V 1 ,…,V n are conjunctive, finding the equivalent rewriting is NP-complete Need only consider rewritings of query length or less

21. Maximally-Contained Rewritings Given: Query Q Rewriting query language L View definitions: V 1 ,…,V n Def. Q’ is a maximally-contained rewriting of Q given V 1 ,…,V n and L if : Q’  L, Q’ ⊑ Q , and there is no Q’’ in L such that Q’ ⊏ Q’’ ⊑ Q More appropriate semantics for mapping definitions under open-world assumption

22. AQUV Algorithms Bucket Algorithm Inverse rules algorithm MiniCon Algorithm All three produce maximally-contained rewritings in L = UCQ for Q, V 1 ,…,V n in CQ CQ: Conjunctive Queries UCQ: Union of CQ’s

23. Bucket Algorithm Create a bucket for each subgoal g i in the query Q . Fill each bucket with view atoms that contribute to g i (see next slide for further detail) Create rewritings Q j ’ from the cartesian product of the buckets. Discard those rewritings such that: Q j ’ ⋢ Q, and it is not possible to add interpreted atoms such that the resulting rewriting is contained in Q .

24. To decide whether a view V should be in the bucket of a subgoal g of Q , consider each of the subgoals v i in V and do the following Terminology: C ( Q ), C ( V ): the interpreted atoms (e.g. >, ≥) of Q , V θ h(V ) : the same as θ but restricted to the head variables in V If A = p (a 1 ,…,a k ,…a n ), then A [k] = a k Filling the Bucket for each v i n V if there is a unifier θ such that θ ( g ) = θ ( v i ) then if ( is_satifiable ( θ h(V ) ( C ( Q ))  θ h(V ) ( C ( V )) and  j is_varible ( g [j]) and  k head ( Q )[k] == g [j]  is_varible ( v i [j]) and  m v i [j] == head ( V )[m] then insert θ ( head ( V )) into the bucket of g end for each

25. Bucket Algorithm: Example View atoms that can contribute to g 1 : V 1 (ID,year), V 2 (ID,A’), V 4 (ID,D’,year) g 1 g 2 g 3

26. Bucket Algorithm: Example (cont.) V 3 (ID,amount) cannot contribute to g 2 : amount ≥ $200M  amount  $50M V 4 (ID,D’,year) V 2 (ID,amount) V 2 (ID,A’) V 4 (ID,Dir,Y’) V 1 (ID,Y’) V 1 (ID,year) g 3 g 2 g 1

27. Bucket Algorithm: Example (cont.) V 1 and V 4 are mutually disjoint… V 4 (ID,D’,year) V 2 (ID,amount) V 2 (ID,A’) V 4 (ID,Dir,Y’) V 1 (ID,Y’) V 1 (ID,year) g 3 g 2 g 1

28. The Inverse Rules Algorithm Given: Query Q View definitions: V 1 ,…,V n Return where each is an inverse rule for V j

29. The Inverse Rules Algorithm: Example Q(D,A)  Director(T, D), Actor(T, A) V 1 (T, Y, D)  Movie(T, Y, ‘comedy’), Director(T, D) V 2 (T, A)  Movie(T, Y, G), Actor(T, A) f1(T, A) , f2(T, A) : Skolem functions Movie(T, Y, ‘comedy’)  V 1 (T, Y, D) Director(T, D)  V 1 (T, Y, D) Movie(T, f 1 (T, A) , f 2 (T, A) )  V 2 (T, A) Actor(T, A)  V 2 (T, A) Q’ = Q 

30. Global-Local-as-View (GLAV) S7 Movies ( MID , title ) MovieDetais ( MID , dir, year ) Q 1 G (t,d,y)  Movie(t, d, ‘comedy’, y), y ≥ 1970 Q S7 (t,d,y)  Movies(i, t), MovieDetais(i, d, y) Movie: title, director, year, genre Q S7 (t,d,y)  Q 1 G (t,d,y)

31. GLAV: Formalization A set of expressions of the form: or closed-world assumption open-world assumption Q G : query over mediated schema Q S : query over data sources

32. Query Reformulation in GLAV Given a query Q posed over the mediated schema a set of queries (views) over the mediated schema a set of queries (views) over source schema a set of GLAV formulas of the form Find a rewriting Q’ over source schemas as follows: Obtain Q 1 by rewriting Q using views Create Q 2 by replacing in Q 1 Obtain Q’ by unfolding in Q 2

33. References A. Y. Halevy. Answering queries using views: A survey . The VLDB Journal, 10. Springer, 2001 M. Lenzerini. Data Integration: A Theoretical Perspective .In Proceedings of PODS’02. ACM, 2002

34. Validation of Mappings between Schemas Guillem Rull Carles Farré Ernest Teniente Toni Urpí

35. Motivation All techniques for building mappings are semi-automatic Building a mapping always requires feedback from a human engineer The engineer needs to validate the mapping That means checking if the mapping satisfies the needs and requirements Few work has been done about validating mappings

36. Purpose Our goal is to validate mappings Allowing the engineer to ask whether the mapping satisfies or not certain desirable properties Applying DB schema-validation techniques Reformulating the mapping desirable properties in terms of the problem of query liveliness checking Using our CQC Method to run the query liveliness tests

37. Initial Setting We consider mappings between two relational schemas. We see a mapping as a set of GLAV formulas M = (F, A, B) denotes a mapping between schemas A and B with the set of formulas F. Each mapping formula in F takes one of the following forms: Q A = Q B Q A  Q B where Q A is a query over schema A, and Q B is a query over schema B.

38. Our Approach: Sketch Define a set of desirable properties of mappings. Reformulate these properties in terms of checking whether a certain query is lively. A query is lively if it admits a non-empty extension. Use the CQC method to perform the liveliness tests.

39. Mapping Properties in terms of Query Liveness Define a new schema S that combines the two mapped schemas. Mapped schemas: A = (DR A , IC A ), B = (DR B , IC B ) Schema S = (DR A  DR B , IC A  IC B ) Make mapping M explicit by means of additional integrity constraints Schema S = (DR A  DR B , IC A  IC B  IC M ) Define a query Q over S such that Desirable mapping property holds for M if and only if Q is lively over S

40. Mapping Properties We have looked for already identified desirable properties of mappings in the literature We have considered two of the properties identified in: Jayant Madhavan, Philip A. Bernstein, Pedro Domingos, Alon Y. Halevy: Representing and Reasoning about Mappings between Domain Models. AAAI/IAAI 2002: 80-86 These properties are: Mapping Inference Query Answerability

41. Mapping Properties We have defined a new property: Mapping Losslessness It is an extension of query answerability Allows us to obtain useful validation information in those cases when query answerability is not useful. We have also considered the property: Mapping Satisfiability (two variants: strong and weak)

42. Mapping Inference Checks whether a given mapping formula is inferred from the other formulas in the mapping. More formally, checks whether every pair of consistent instances that satisfies the mapping already satisfies the given formula.

43. Mapping Satisfiability Strong Satisfiability Checks whether there is a pair of instances that satisfies all mapping formulas in a non-trivial way. Weak Satisfiability Checks whether there is a pair of instances that satisfies at least one mapping formula in a non-trivial way.

44. Query Answerability Checks if the two mapped schemas provide the same answer to a given query More formally, Given a query Q defined over one of the mapped schemas, for instance, the schema A. It checks whether For every consistent instance D B of schema B, and for every pair of consistent instances D A , D A ’ of schema A that are mapped to D B , then Q(D A ) = Q(D A ’) Useless when mapping formulas are like Q A  Q B .

45. Mapping Losslessness Checks whether the mapping captures the information represented by a given query More formally, Let Q be a query over schema A Let M = (F, A, B) the mapping, where F = {V A 1 op V B 1 , …, V A N op V B N } For every consistent instance D B of schema B, and for every pair of consistent instances D A , D A ’ of A that are mapped to D B and such that V A 1 (D A )=V A 1 (D A ’),…, V A N (D A )=V A N (D A ’) , then Q(D A ) = Q(D A ’) It is applicable when formulas are like V A  V B . When mapping formulas are like V A = V B , mapping losslessness and query answerability are equivalent.

46. Example 1 referential constraint employee emp-id category happiness-degree category cat-id salary Schema A emp id salary Schema B queries: qA ( E , S )  employee ( E , C , H )  category ( C , S ) qB ( E , S )  emp ( E , S ) qA  qB

47. Example 1: Query Answerability vs Map. Losslessness Schema A = ( DR A , IC A ), where constraints IC A = { employee ( E , C , H )   S category ( C , S ) } and deductive rules DR A = { qA ( E , S )  employee ( E , C , H )  category ( C , S ) } Schema B = ( DR B ,  ), where deductive rules DR B = { qB ( E , S )  emp ( E , S ) }. Mapping M = ( F , A , B ), where formulas F = { qA  qB }. Query p ( E )  employee ( E , C , H ) Query Answerability does NOT hold: D B = {emp(0, 30), emp(1, 20)} D A = {employee( 0 , 0, 5), category(0, 30 )} D A ’ = {employee( 1 , 0, 5), category(0, 20 )} Mapping Losslessness holds: As all employees in A must have a category because of the referential constraint, query qA captures all employees.

48. Example 2: Mapping Losslessness Schema A = ( DR A , IC A ), where constraints IC A = { employee ( E , C , H )   S category ( C , S ) } and deductive rules DR A = { qA ( E , S )  employee ( E , C , H )  H > 5  category ( C , S ) } Schema B = ( DR B ,  ), where deductive rules DR B = { qB ( E , S )  emp ( E , S ) }. Mapping M = ( F , A , B ), where formulas F = { qA  qB }. Query p ( E )  employee ( E , C , H ) Mapping Losslessness does NOT hold: D B = {emp(0, 20)} D A = {employee(0, 0, 10), category(0, 20), employee(1, 1, 4), category(1, 30) } D A ’ = {employee(0, 0, 10), category(0, 20) , employee(2, 1, 4), category(1, 10) } qA(D A ) = qA(D A ’) = {qA(0, 20)} p(D A ) = {p(0, 20), p(1, 30)}  p(D A ’) = {p(0, 20), p(2, 10)}

49. Example 2: Map. Lossleness in terms of Query Liveliness Mapping M is lossless with respect to Q if and only if map_loss is not lively on this schema. Deductive rules: map_loss  p ( X )  ¬ p' ( X ) p ( E )  employee ( E , C , H ) qA ( E , S )  employee ( E , C , H )  H > 5  category ( C , S ) qB ( E , S )  emp ( E , S ) p' ( E )  employee' ( E , C , H ) qA' ( E , S )  employee' ( E , C , H )  H > 5  category' ( C , S ) DR A DR B DR A ' Constraints : employee ( E , C , H )   S category ( C , S ) employee' ( E , C , H )   S category' ( C , S ) qA ( X , Y )  qA' ( X , Y ) qA' ( X , Y )  qA ( X , Y ) qA ( X , Y )  qB ( X , Y ) IC A IC A ' IC L IC M

50. References J. Madhavan, P. A. Bernstein, P. Domingos, A. Y. Halevy: Representing and Reasoning about Mappings between Domain Models. AAAI/IAAI 2002: 80-86 G. Rull, C. Farré, E. Teniente, T. Urpí: Validation of mappings between schemas. Data & Knowledge Engineering 66(3): 414-437 (2008)