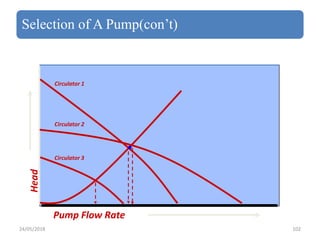
This document provides an overview of pumps and centrifugal pumps specifically. It begins with classifications of pumps, including rotodynamic, reciprocating, and rotary positive displacement pumps. It then focuses on centrifugal pumps, describing their main components like the impeller and casing. Centrifugal pumps are further classified based on flow direction and head. The working principle is explained using velocity diagrams and equations for pressure developed. Hydraulic analysis defines terms like static head and manometric head. Energy transfer in the impeller and pump efficiencies are also covered.