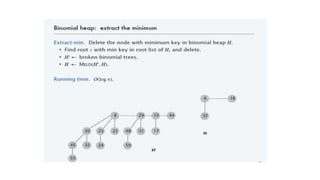
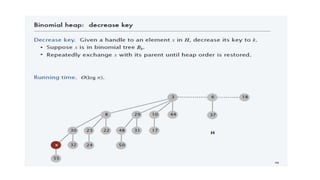
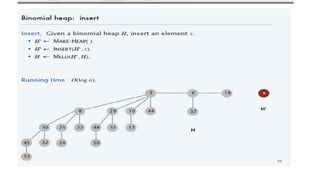
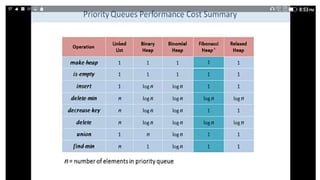
A Fibonacci heap is a data structure used to implement priority queues. It is composed of a collection of heap-ordered trees that store minimum priority elements. Each node stores a key-value and pointers to its parent and children. Operations like insertion, deletion, and decreasing key values are performed using cuts, melds, and tree rotations to maintain the heap properties. Fibonacci heaps support these operations in amortized O(1) time through techniques like lazy merging of trees and path compression. They are useful for graph algorithms like Dijkstra's and Prim's algorithms that require efficient priority queue operations.

1. BINOMIAL HEAP

2. • A Binomial Heap is a collection of Binomial Trees.
• a binomial heap is a heap similar to a binary heap but also supports
quick merging of two heaps.
• This is achieved by using a special tree structure. It is important as an
implementation of the mergeable heap abstract data type (also called
meldable heap), which is a priority queue supporting merge
operation.

3. Structure of a binomial heap
• A binomial heap is implemented as a set of binomial trees that satisfy
the binomial heap properties:
• Each binomial tree in a heap obeys the minimum-heap property: the
key of a node is greater than or equal to the key of its parent.
• Atmost one binomial tree whose root degree is ‘K’
• There can only be either one or zero binomial trees for each order,
including zero order.

4. Introduction to Binomial Tress
• A binomial heap is implemented as a collection of binomial trees
• A binomial tree of order k has 2k nodes, height k.
• It is an ordered tree
• It is set of binomial tree and Binomial Tree Bk is an ordered tree
• A binomial heap is implemented as a collection of binomial trees (compare with
a binary heap, which has a shape of a single binary tree), which are defined
recursively as follows:
• A binomial tree of order 0 is a single node
• A binomial tree of order k has a root node whose children are roots of binomial
trees of orders k−1, k−2, ..., 2, 1, 0 (in this order).

5. Properties of Binomial Tree Bk
1. Bktreehas2k
nodes
2. DegreeofrootisK
3. Height=k
4. ThereareexactlyK
CI nodesatdepthiwhereK
CI = K!
(K-i)!*I!

6. Implementation
• Because no operation requires random access to the root nodes of
the binomial trees, the roots of the binomial trees can be stored in a
linked list, ordered by increasing order of the tree.
Merge
As mentioned above, the simplest and most important operation
is the merging of two binomial trees of the same order within a
binomial heap.
1. As their root node is the smallest element within the tree, by
comparing the two keys, the smaller of them is the minimum key,
and becomes the new root node.
2. Then the other tree becomes a subtree of the combined tree. This
operation is basic to the complete merging of two binomial heaps

8. Insert
Inserting a new element to a heap can be done by simply creating a new heap
containing only this element and then merging it with the original heap.
Due to the merge, insert takes O(log n) time. However, across a series of n
consecutive insertions, insert has an amortized time of O(1) (i.e. constant).
Find minimum
• To find the minimum element of the heap, find the minimum among the roots of
the binomial trees. This can again be done easily in O(log n) time, as there are just
O(log n) trees and hence roots to examine.
Delete minimum
• To delete the minimum element from the heap, first find this element, remove it
from its binomial tree, and obtain a list of its subtrees. Then transform this list of
subtrees into a separate binomial heap by reordering them from smallest to largest
order.
• Then merge this heap with the original heap. Since each tree has at most log n
children, creating this new heap is O(log n). Merging heaps is O(log n), so the entire
delete minimum operation is O(log n).

9. Decrease key
• After decreasing the key of an element, it may become smaller than
the key of its parent, violating the minimum-heap property.
• If this is the case, exchange the element with its parent, and possibly
also with its grandparent, and so on, until the minimum-heap
property is no longer violated.
• Each binomial tree has height at most log n, so this takes O(log n)
time.

18. B TREE

19. Introduction
• In B-trees, internal (non-leaf) nodes can have a variable
number of child nodes within some pre-defined range. When
data is inserted or removed from a node, its number of child
nodes changes. In order to maintain the pre-defined range,
internal nodes may be joined or split.
• Because a range of child nodes is permitted, B-trees do not
need re-balancing as frequently as other self-balancing search
trees, but may waste some space, since nodes are not entirely
full. The lower and upper bounds on the number of child
nodes are typically fixed for a particular implementation

20. Cont..
• Each internal node of a B-tree will contain a number of keys.
The keys act as separation values which divide its sub trees.
For example, if an internal node has 3 child nodes (or
subtrees) then it must have 2 keys: a1 and a2. All values in the
leftmost subtree will be less than a1, all values in the middle
subtree will be between a1 and a2, and all values in the
rightmost subtree will be greater than a2.

21. Advantages of B-tree usage for databases
• The B-tree uses all of the ideas described above. In particular, a B-
tree:
• keeps keys in sorted order for sequential traversing
• uses a hierarchical index to minimize the number of disk reads
• uses partially full blocks to speed insertions and deletions
• keeps the index balanced with an elegant recursive algorithm
• In addition, a B-tree minimizes waste by making sure the interior
nodes are at least half full. A B-tree can handle an arbitrary number of
insertions and deletions.

22. Definition
• According to Knuth's definition, a B-tree of order m is a tree which
satisfies the following properties:
• Every node has at most m children.
• Every non-leaf node (except root) has at least ⌈m/2⌉ children.
• The root has at least two children if it is not a leaf node.
• A non-leaf node with k children contains k−1 keys.
• All leaves appear in the same level

23. B-trees and B+ trees

24. Motivation
• To have dynamic indexing structures that can evolve when records are
added and deleted
• Not the case for static indexes
• Would have to be completely rebuilt
• Optimized for searches on block devices
• Both B trees and B+ trees are not binary
• Objective is to increase branching factor (degree or fan-out) to reduce the
number of device accesses

25. B trees
• Generalization of binary search trees
• Not binary trees
• The B stands for Bayer (or Boeing)
• Designed for searching data stored on block-oriented devices

26. A very small B tree
Bottom nodes are leaf nodes: all their pointers
are NULL

27. In reality
In
tree
ptr
Key
Data ptr
In
tree
ptr
Key
Data ptr
In
tree
ptr
Key
Data ptr
In
tree
ptr
Key
Data ptr
In
tree
ptr
To
Leaf
7
To
leaf
16
To
Leaf
--
Null
Null
--
Null
Null

28. B+ trees
• Variant of B trees
• Two types of nodes
• Internal nodes have no data pointers
• Leaf nodes have no in-tree pointers
• Were all null!

30. Example B+-tree
9
5
1 3 5 6 30 40
9 16 17
16 30
 index node
 leaf/data node

31. B+ Tree
• Only leave node has record pointer
• No record pointer in every node
• Each leave node has copy of node
• It uses more spaces than B tree
• Internal Nodes stores only key values
• All leaf nodes ‘r’ are interconnected each other for fast
access
• Key is used to search the proper key
• B+ tree combines feature of ISAM and B tree.

32. B+ tree nodes
In
tree
ptr
Key
In
tree
ptr
Key
In
tree
ptr
Key
In
tree
ptr
Key
In
tree
ptr
Key
In
tree
ptr
Key
Data ptr
Key
Data ptr
Key
Data ptr
Key
Data ptr
Key
Data ptr
Key
Data ptr

33. Importance
• B Tree are used in file systems to allow quick random access
to an arbitrary block in a particular file. The basic problem is
turning the file block i address into a disk block (or perhaps
to a cylinder-head-sector) address.
• MS-DOS
• File Allocation Table (FAT)
• FAT12 file system

34. B+ trees are used by
• NTFS, ReiserFS, NSS, XFS, JFS, ReFS, and BFS file
systems for metadata indexing
• BFS for storing directories.
• IBM DB2, Informix, Microsoft SQL Server, Oracle 8,
Sybase ASE, and SQLite for table indexes

35. Disjoint set data structure

36. Introduction
• grouping n distinct elements into a collection of disjoint sets.
• No common elements in two different sets/
• A disjoint-set data structure maintains a collection S = {S1, S2, . . . ,Sk}
of disjoint dynamic sets. Each set is identified by a representative,
which is some member of the set.
• rule for choosing the representative, such as choosing the smallest
member in the set
• Set of elements partitioned into no of disjoint subset

37. Operations
• MAKE-SET(x) creates a new set whose only member (and thus
representative) is pointed to by x. Since the sets are disjoint, we
require that x not already be in a set.
• UNION(x, y) unites the dynamic sets that contain x and y, say Sx and
Sy, into a new set that is the union of these two sets.
• The two sets are assumed to be disjoint prior to the operation. The
representative of the resulting set is some member of Sx U Sy,
although many implementations of UNION choose the representative
of either Sx or Sy, as the new representative.
• FIND-SET(x) returns a pointer to the representative of the (unique) set
containing x.

38. Linked List representation of DJS
• Linked-list representations of two sets.
• One contains objects b, c, e, and h, with c as the representative, and
the other contains objects d, f, and g, with f as the representative.
• Each object on the list contains a set member, a pointer to the next
object on the list, and a pointer back to the first object on the list,
which is the representative.

40. Disjoint-set forests
• In a faster implementation of disjoint sets, we represent sets by
rooted trees, with each node containing one member and each tree
representing one set.
• The root of each tree contains the representative and is its own
parent
• As we shall see, although the straightforward algorithms that use this
representation are no faster than ones that use the linked-list
representation, by introducing two heuristics--"union by rank" and
"path compression“
• we can achieve the asymptotically fastest disjoint-set data structure
known, and improve the optimization also

41. We perform the three disjoint-set operations as follows. A MAKE-SET
operation simply creates a tree with just one node. We perform a FIND-SET
operation by chasing parent pointers until we find the root of the tree. The
nodes visited on this path toward the root constitute the find path

42. Heuristics to improve the running time
• The first heuristic, union by rank, is similar to the weighted-union
heuristic we used with the linked-list representation. The idea is to
make the root of the tree with fewer nodes point to the root of the
tree with more nodes.
• The second heuristic, path compression, is also quite simple and very
effective. we use it during FIND-SET operations to make each node
on the find path point directly to the root. Path compression does not
change any ranks.
• Analysis of union by rank with path compression O(m lg* n).

44. Discuss about
• Disjoint sets and operations
• Detecting the Cycle
• Graphical Representation
• Array Implementation
• Weighted union and collapsing find…

45. • Disjoint set operations
1. Make Set - c
2. FIND
3. UNION
• Detecting the Cycles
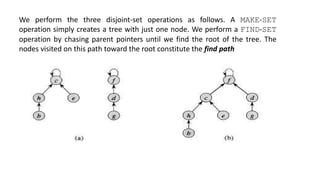
DSJ is useful for detecting the Cycle in undirected graph. Example Kruskal’s
Algorithm, If the set consist of elements in same sets, lets say cycle.
• Disjoint set using Sets
• Disjoint set using Graph representation [weighted Union, and Find
Collapsing]
• Disjoint set using Array
• Disjoint set using Rank and Path Compression

46. Fibonacci Heaps

47. Introduction
• Called a lazy data structure
• Delay work for as long as possible
• Collection of heap ordered Trees
• Each Tree is rooted but unordered
• It maintains pointer to minimum elements
• It set marked nodes
• Each node X has pointed p[X] to its parent and child [X] to one of its
children
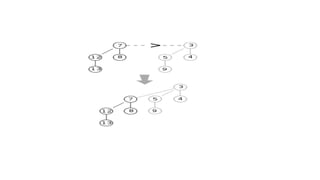
• Fibonacci heaps, in fact, are loosely based on binomial heaps
• Children are linked together represents by circular, doubly linked list.

48. Applications
• Graph Searching – Dijkstra’s Algorithm, Prim’s Algorithm
• Event Driven simulation - Queue
• Statistics- find largest and smallest values
• Graph Problems
• Computing Minimum spanning Trees
• Single source shortest path

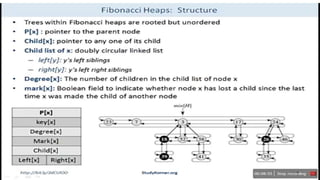
51. Properties and Notations used in Fibonacci
heaps
1. Set of Heap ordered trees
2. Maintain pointer to minimum element Properties
3. Set of marked nodes
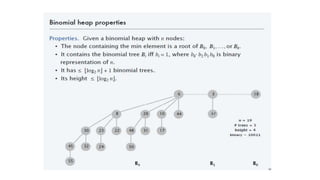
• n[H] = number of nodes in heap.
• degree/rank(x) = number of children of node x.
• degree/ rank(H) = max rank of any node in heap H. Notations
• trees(H) = number of trees in heap H.
• marks(H) = number of marked nodes in heap H.
• Min (H)= minimum key in heap

53. Amortized Potential function
• For the amortized running time analysis we use the potential method,
in that we pretend that very fast operations take a little bit longer
than they actually do .
• The amount of time saved for later use is measured at any given
moment by a potential function. The potential of a Fibonacci heap is
given by
•Ф ( H) = Trees (H) + 2 * Marks(H)

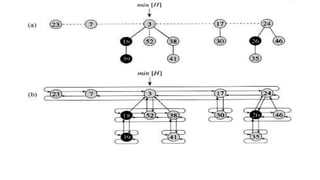
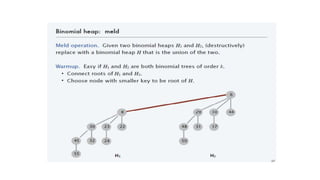
55. Create Fibonacci heaps
n[H] = 0 and min[H] = NIL; there are no trees in H.
Because t (H) = 0 and m(H) = 0, the potential of the empty Fibonacci
heap is Ф(H) = 0.
The amortized cost of MAKE-FIB-HEAP is thus equal to its O(1) actual
cost.
Steps:
1. Set of heap-ordered trees.
2. Maintain pointer to minimum element.
3. Set of marked nodes.

56. 1. Insert
Steps
• Create a new singleton tree.
• Add to root list; update min pointer (if necessary).
2. Merge / Linking Operation
• Linking operation. Make larger root be a child of smaller root.
3. Delete Min
Steps Delete min.
• Delete min; meld its children into root list; update min.
• Consolidate trees so that no two roots have same rank.
• Actual cost. O(rank(H)) + O(trees(H))
4. Decrease Key Steps
1. Decrease key of x.
2. Cut tree rooted at x, meld into root list, and unmark.
3. If parent p of x is unmarked (hasn't yet lost a child), mark it;
Otherwise, cut p, meld into root list, and unmark (and do so
recursively for all ancestors that lose a second child).