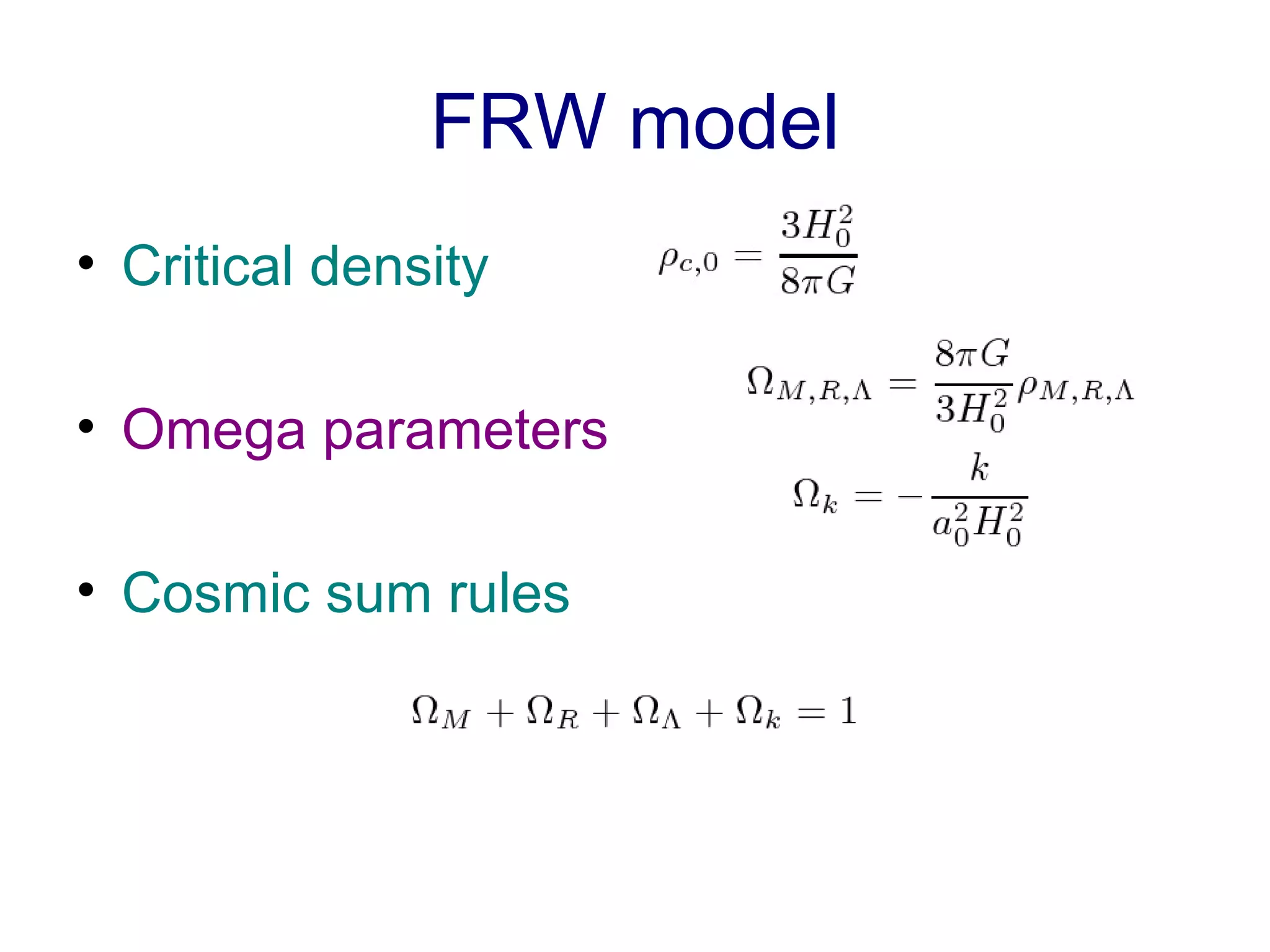
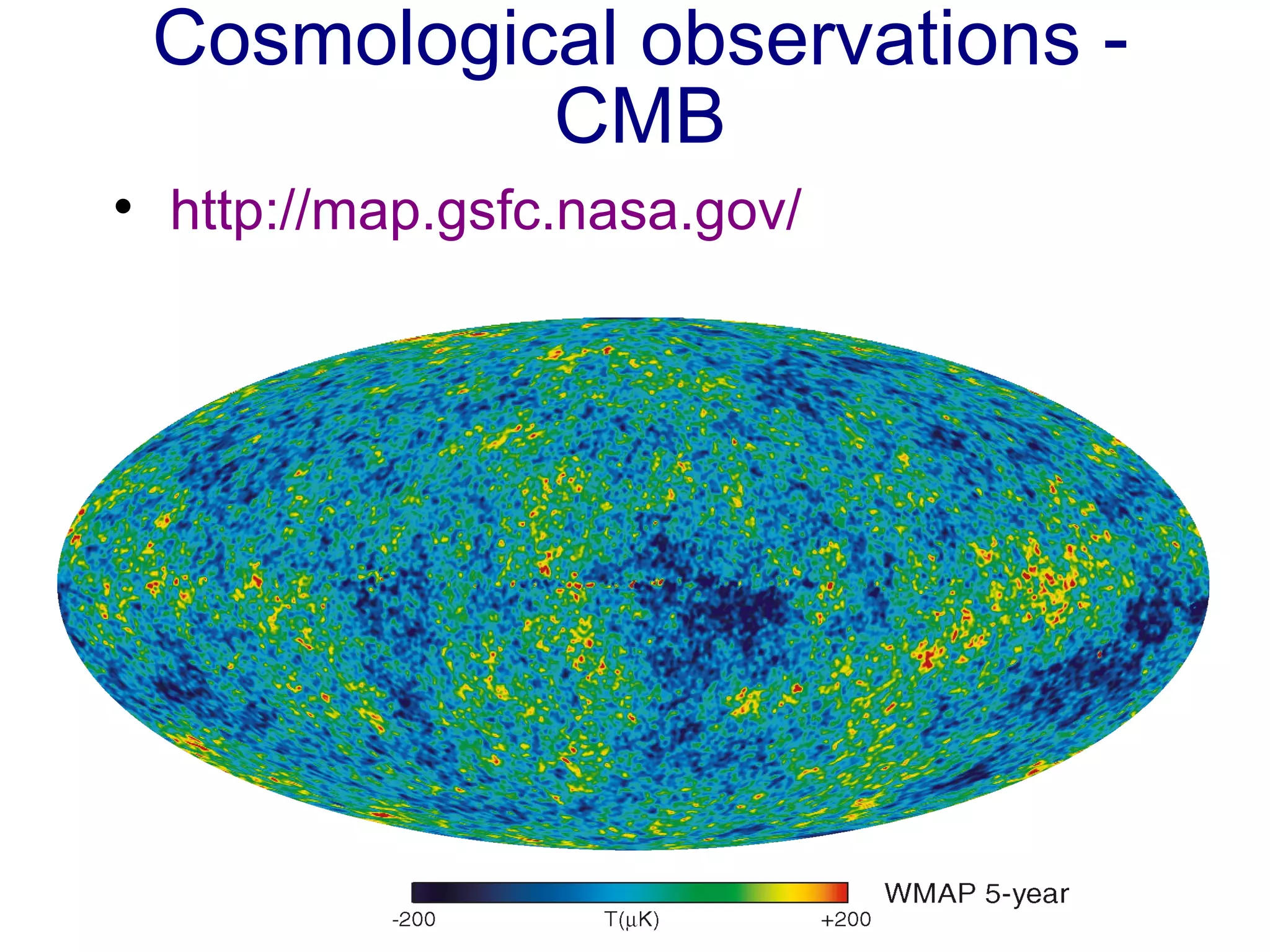
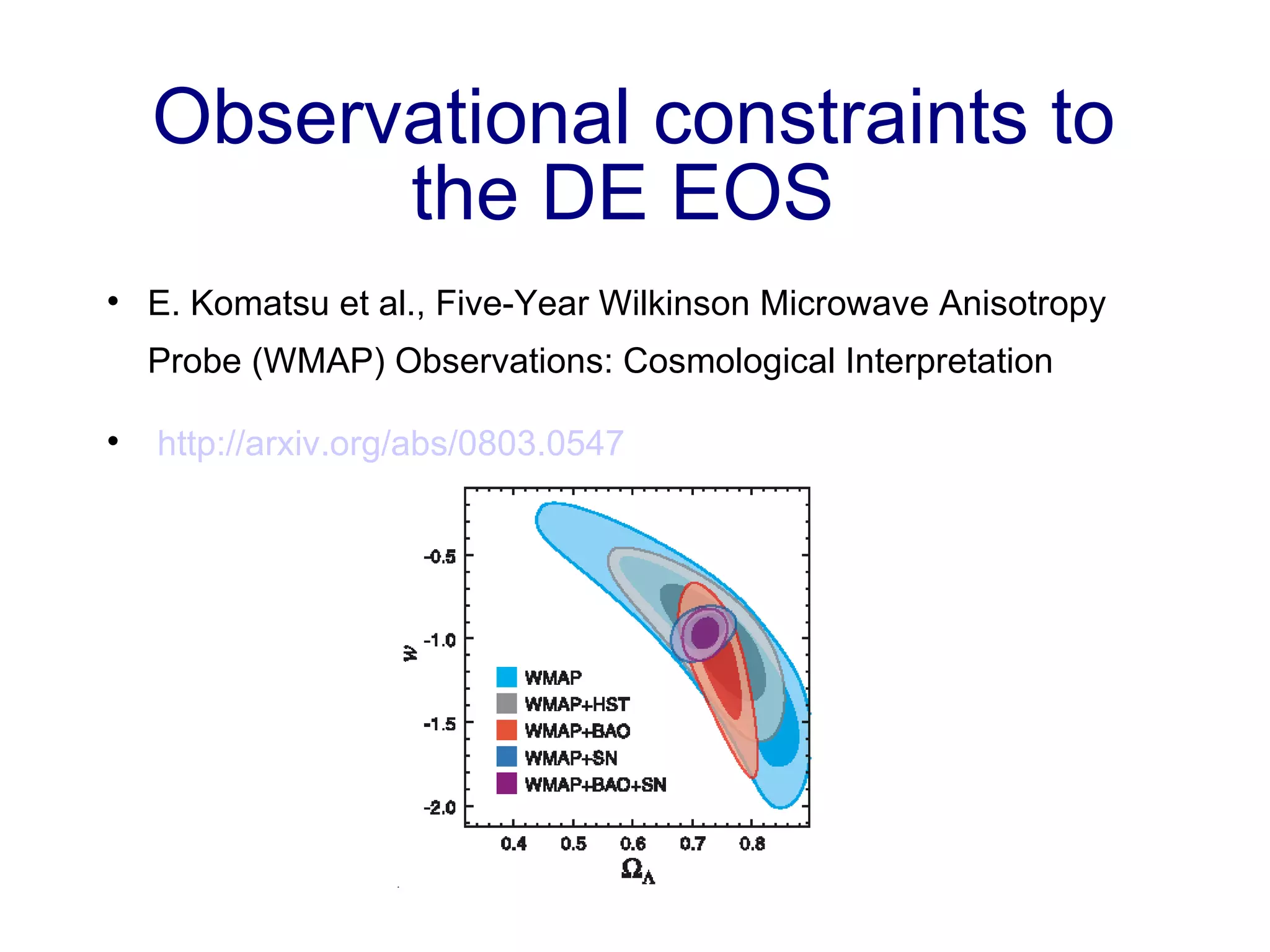
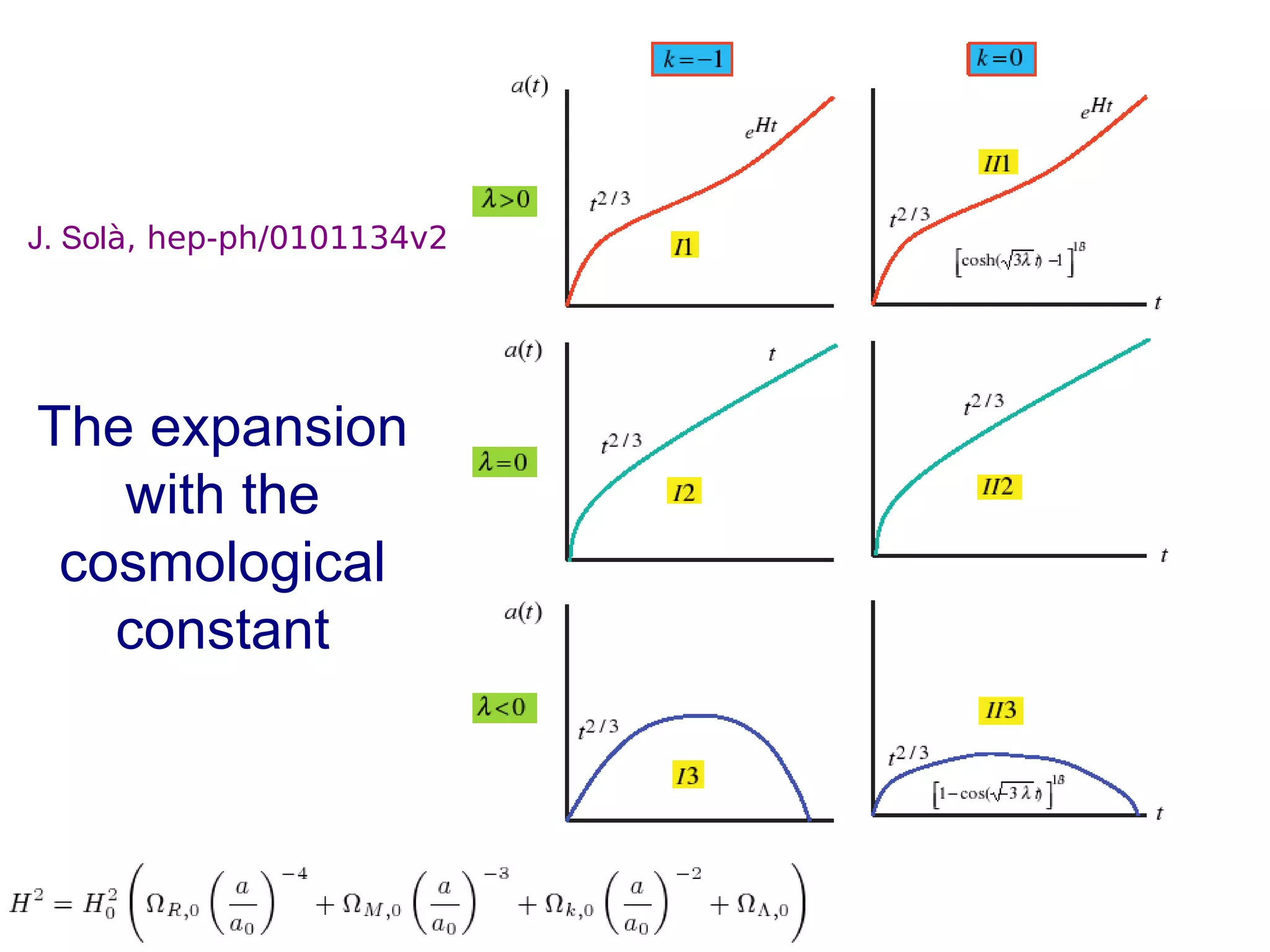
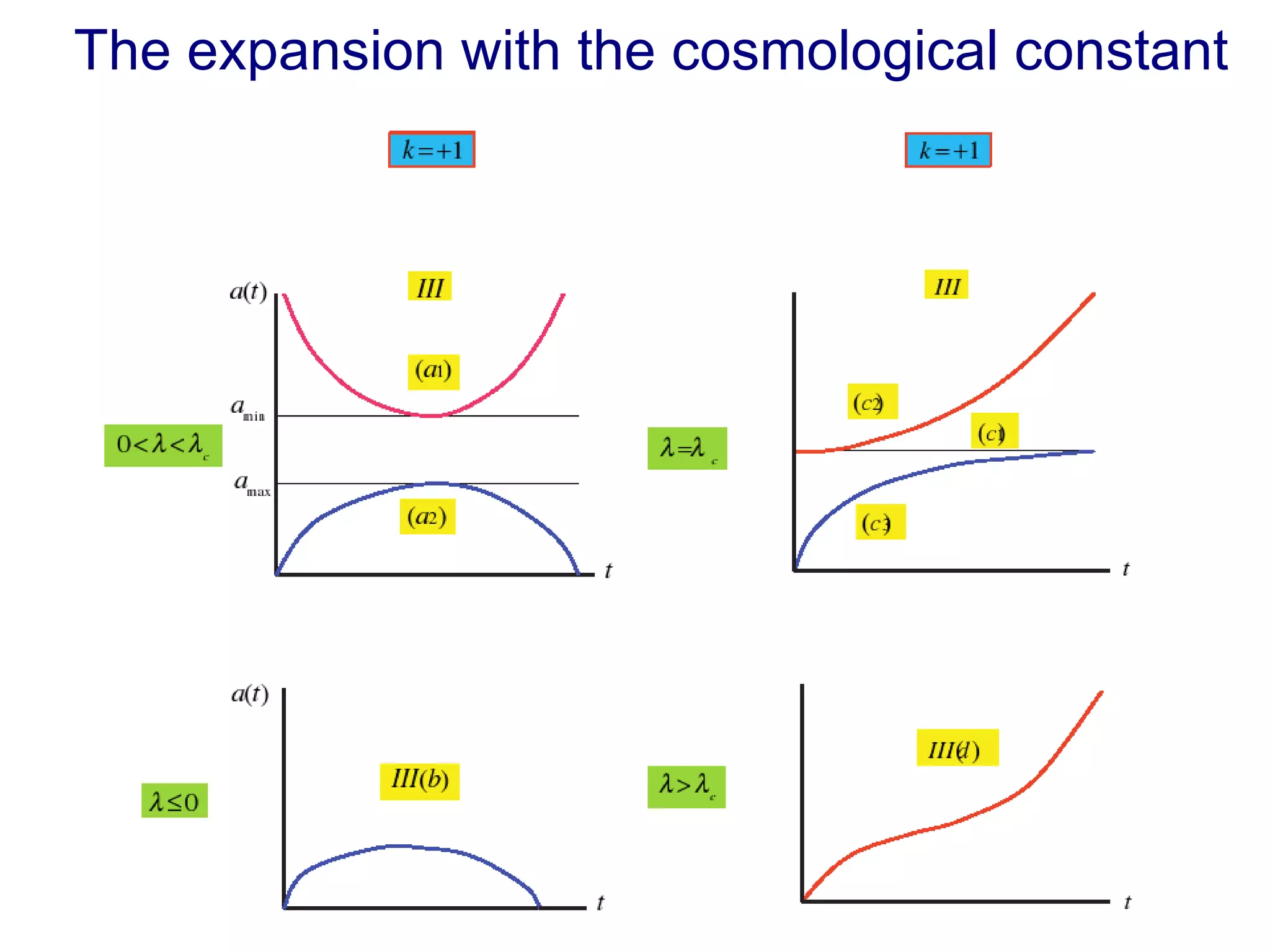
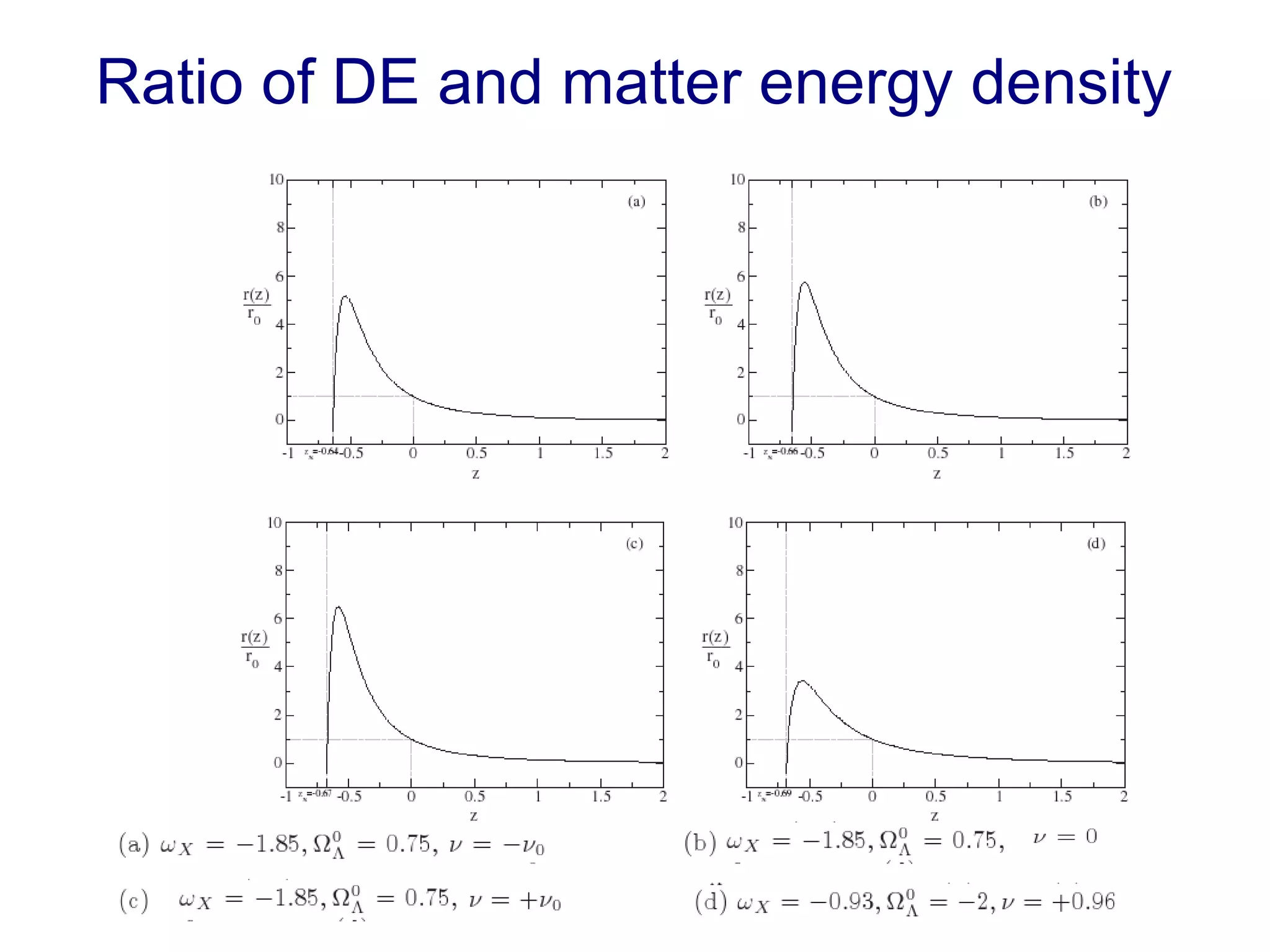
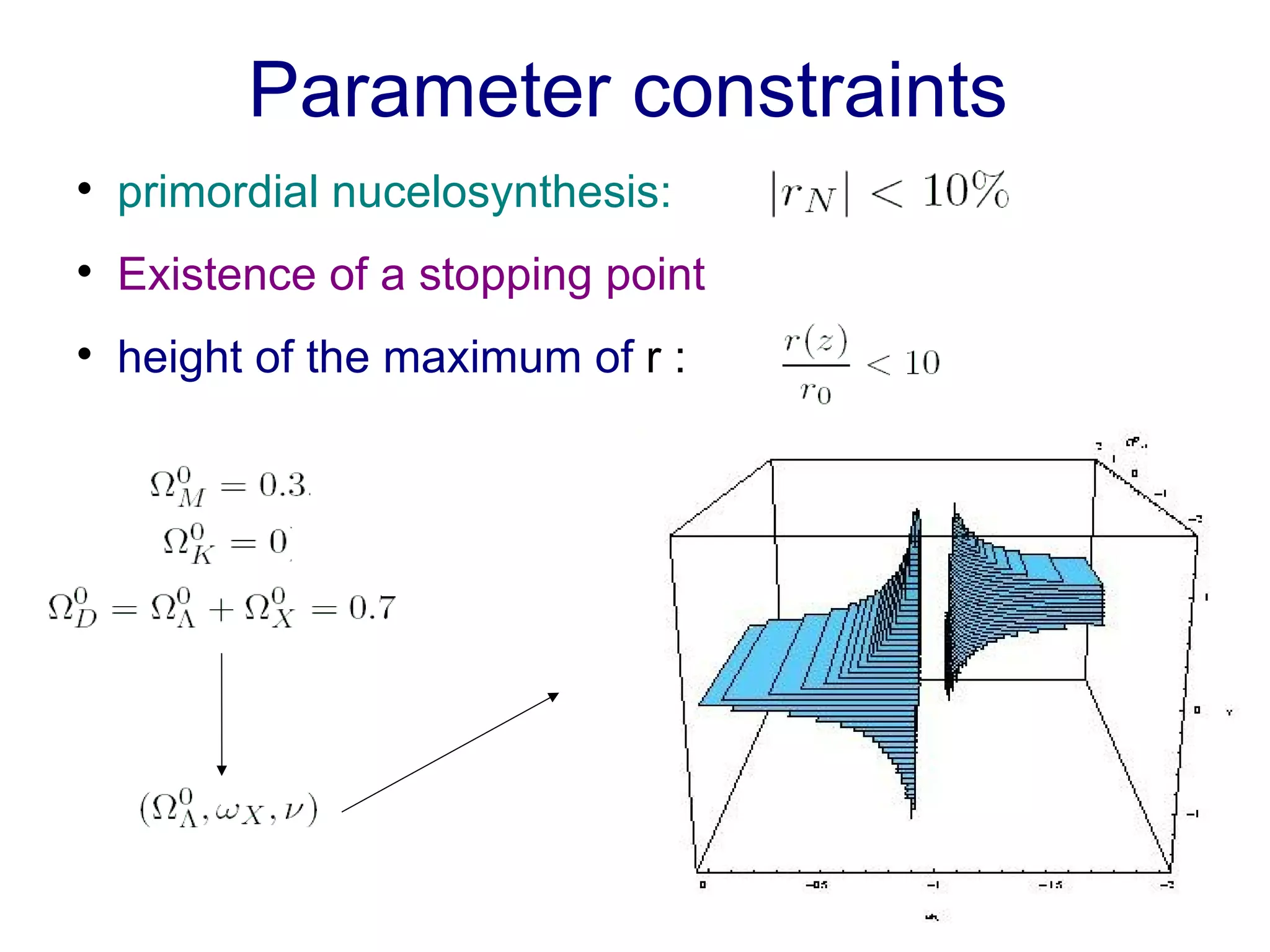
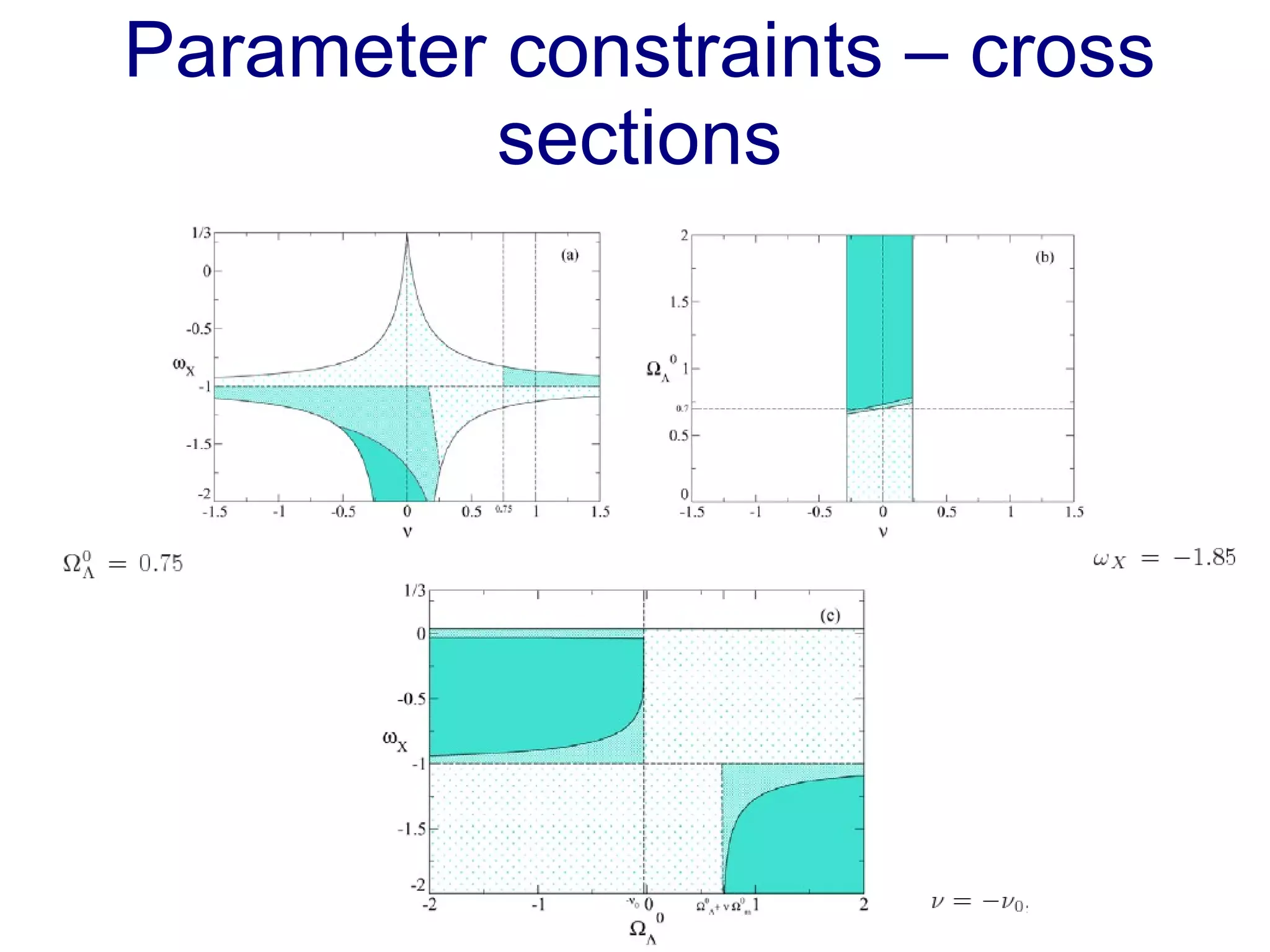
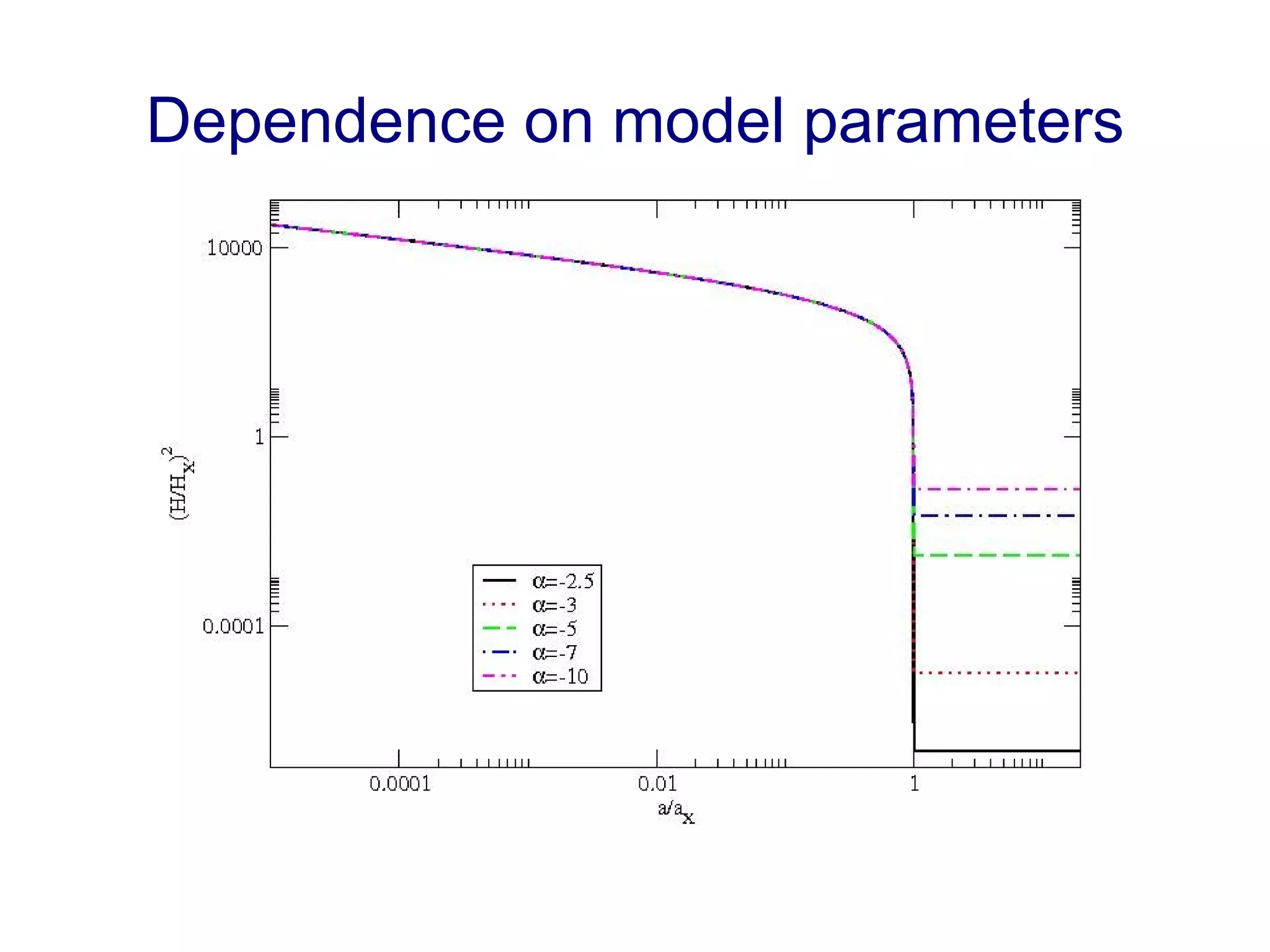
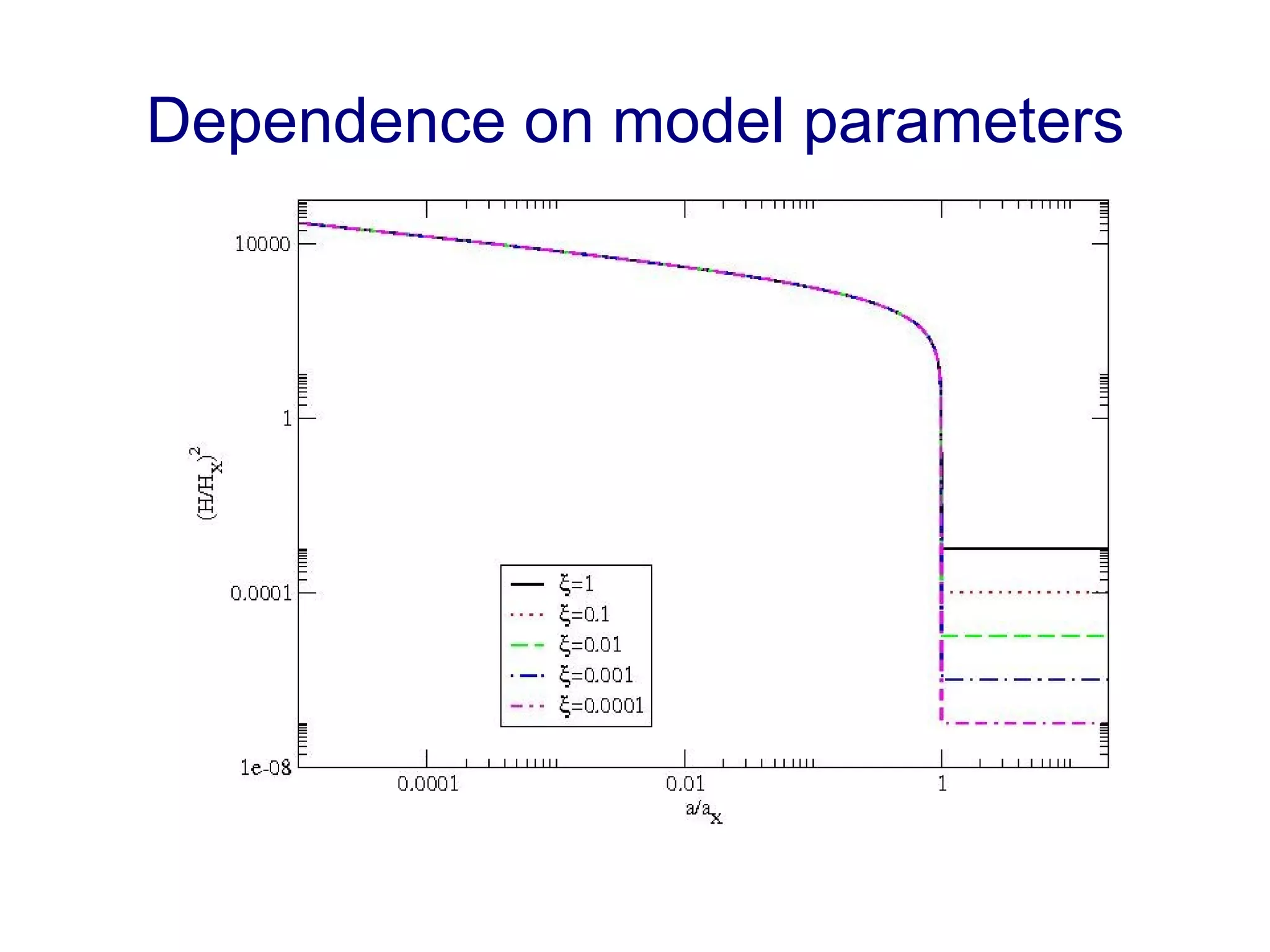
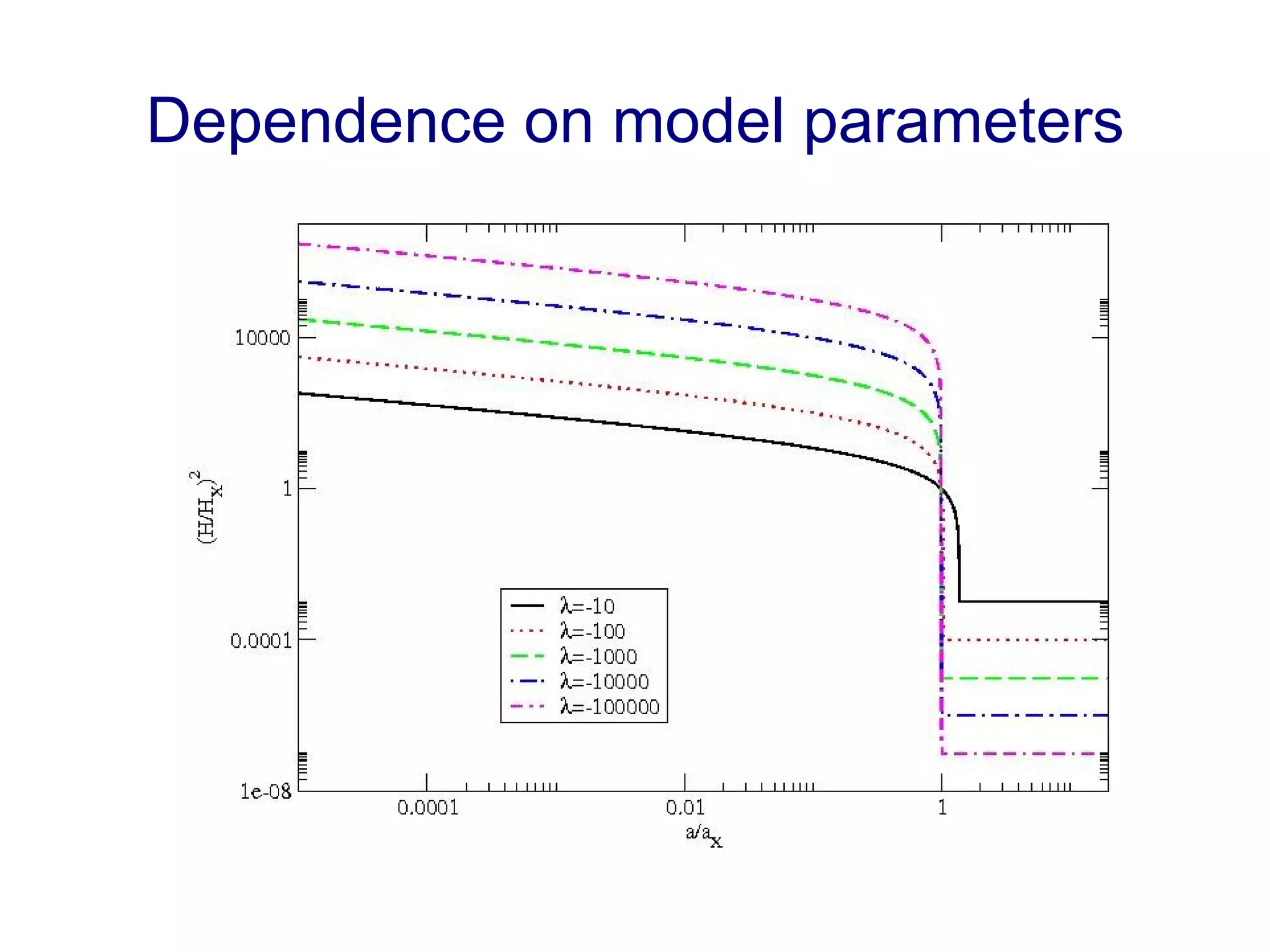
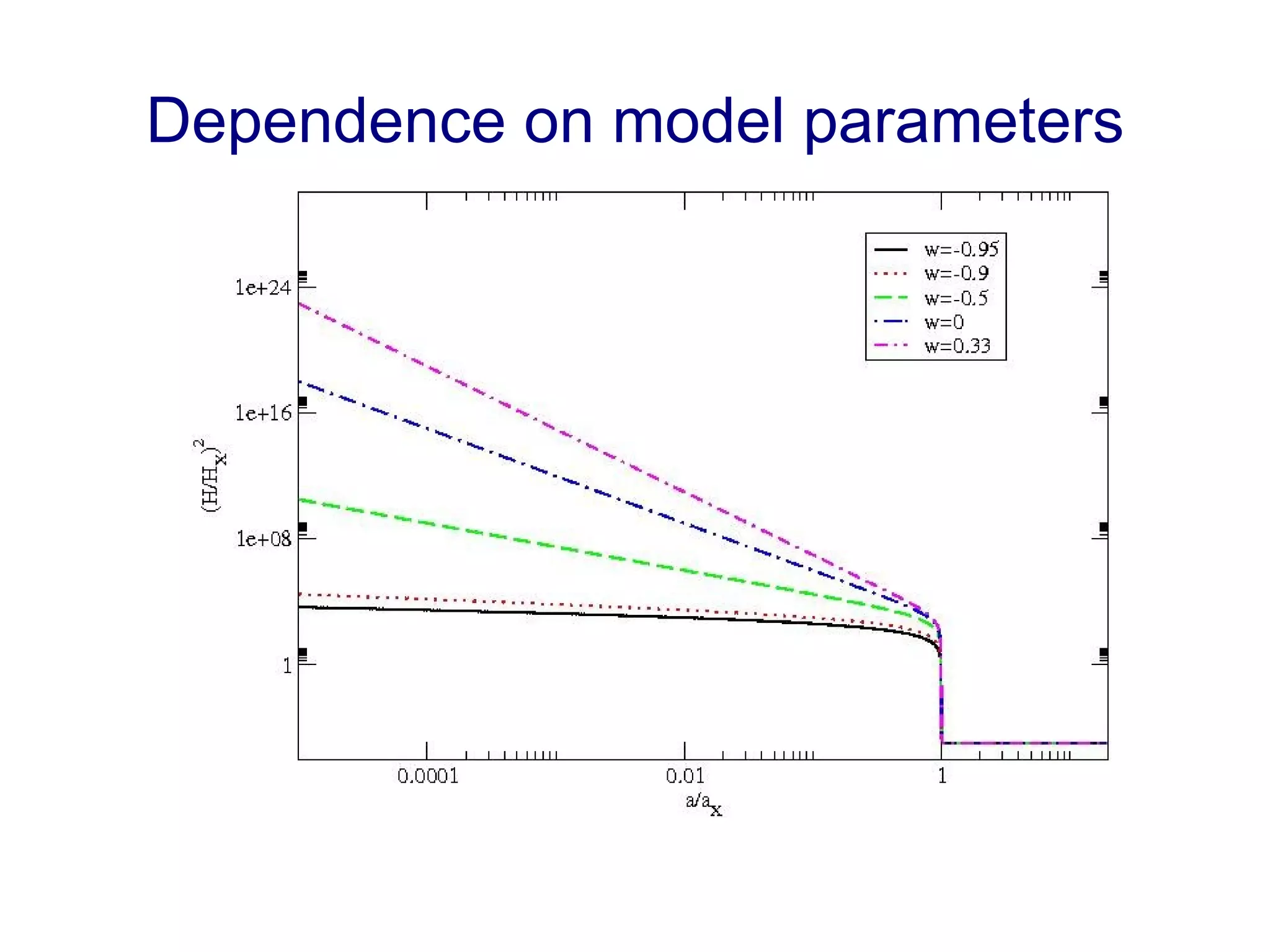
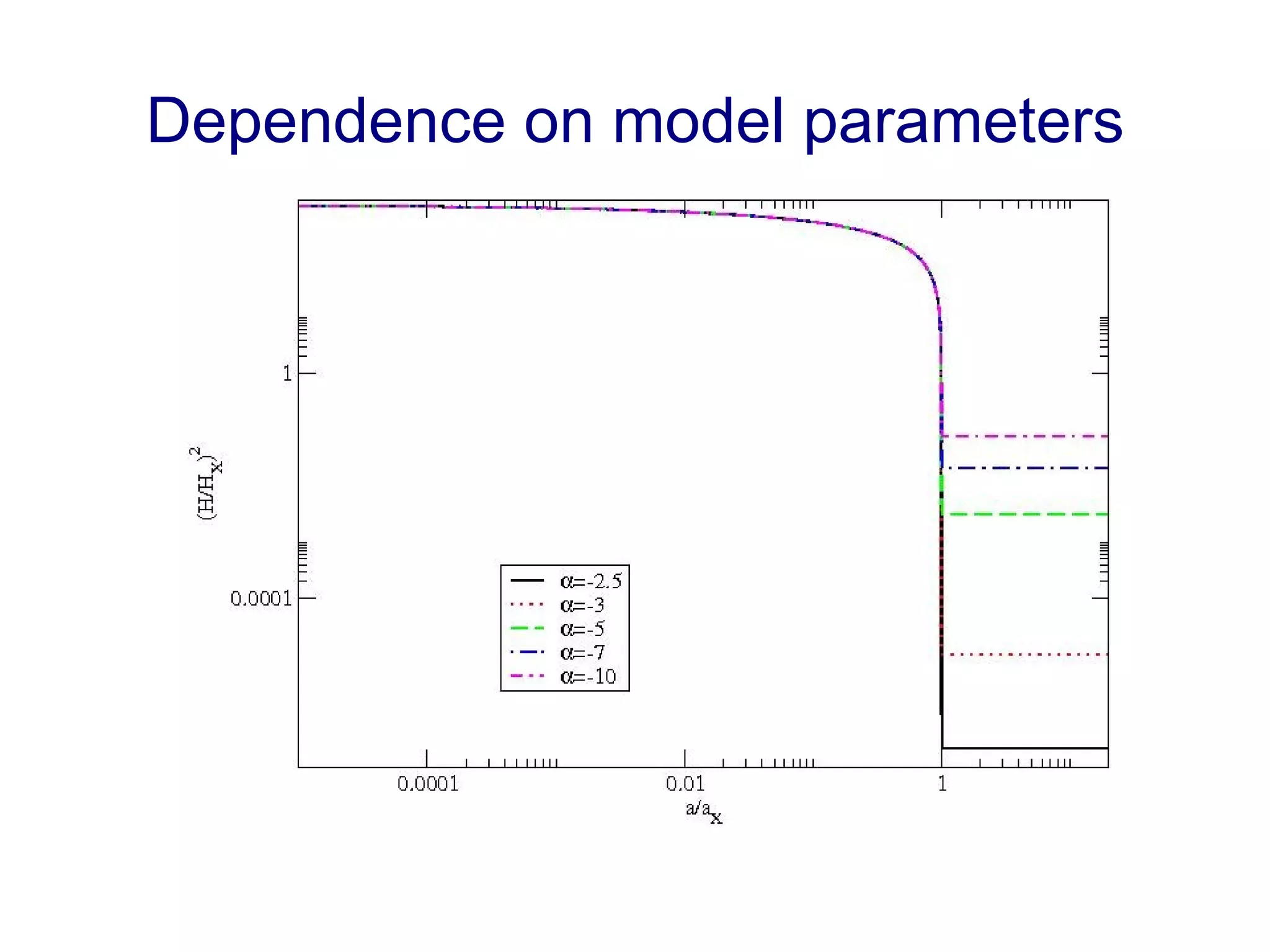
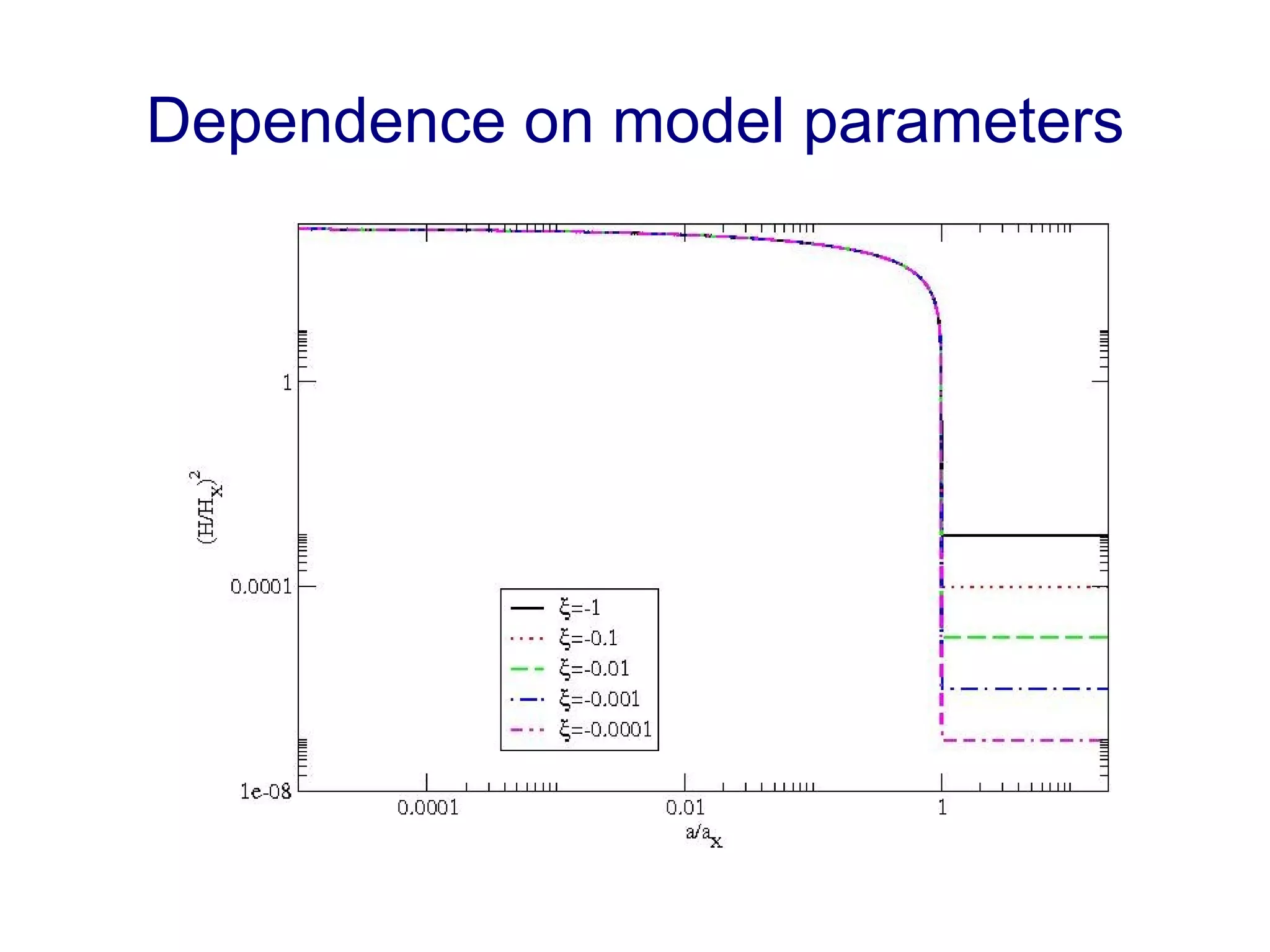
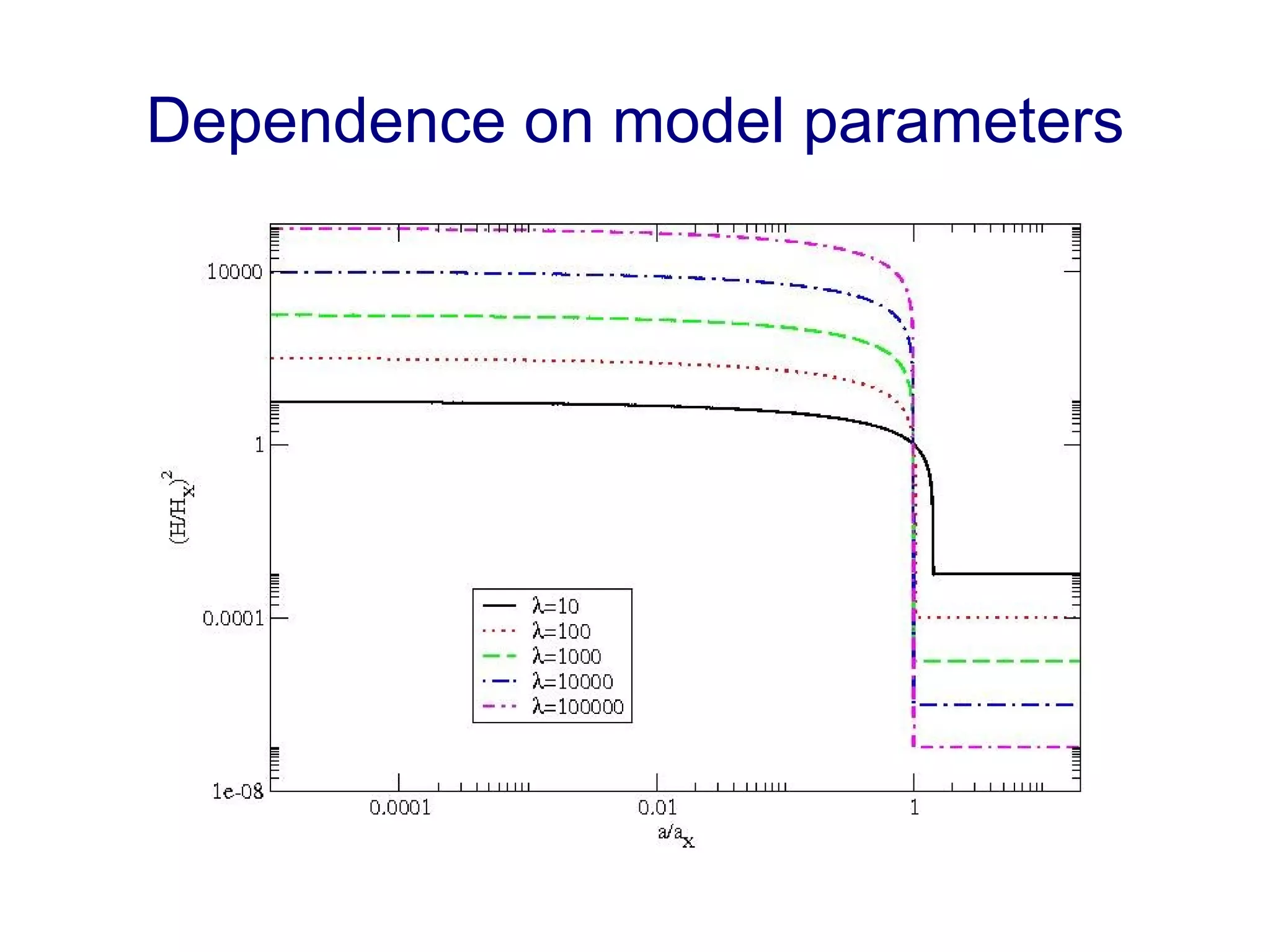
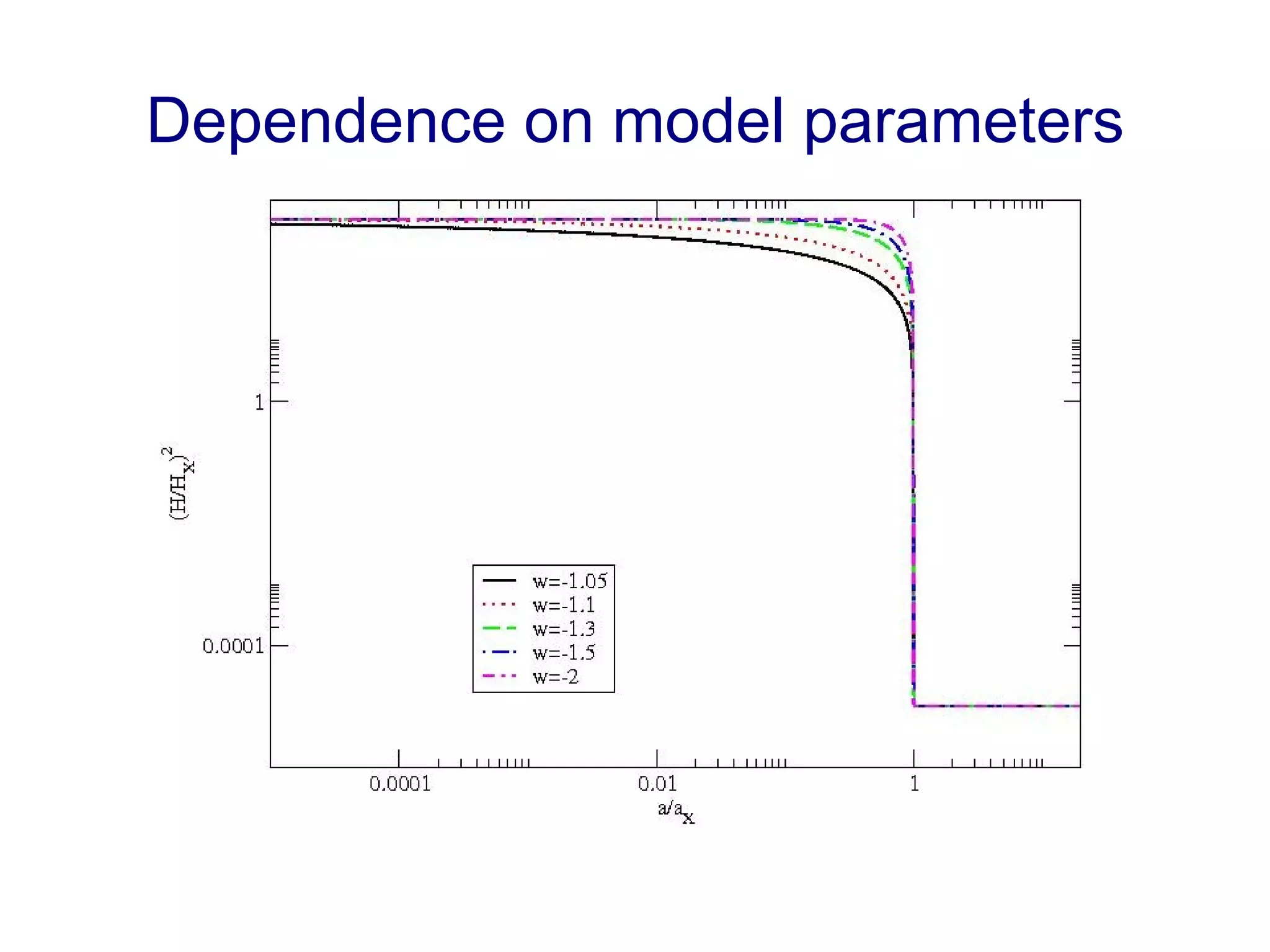
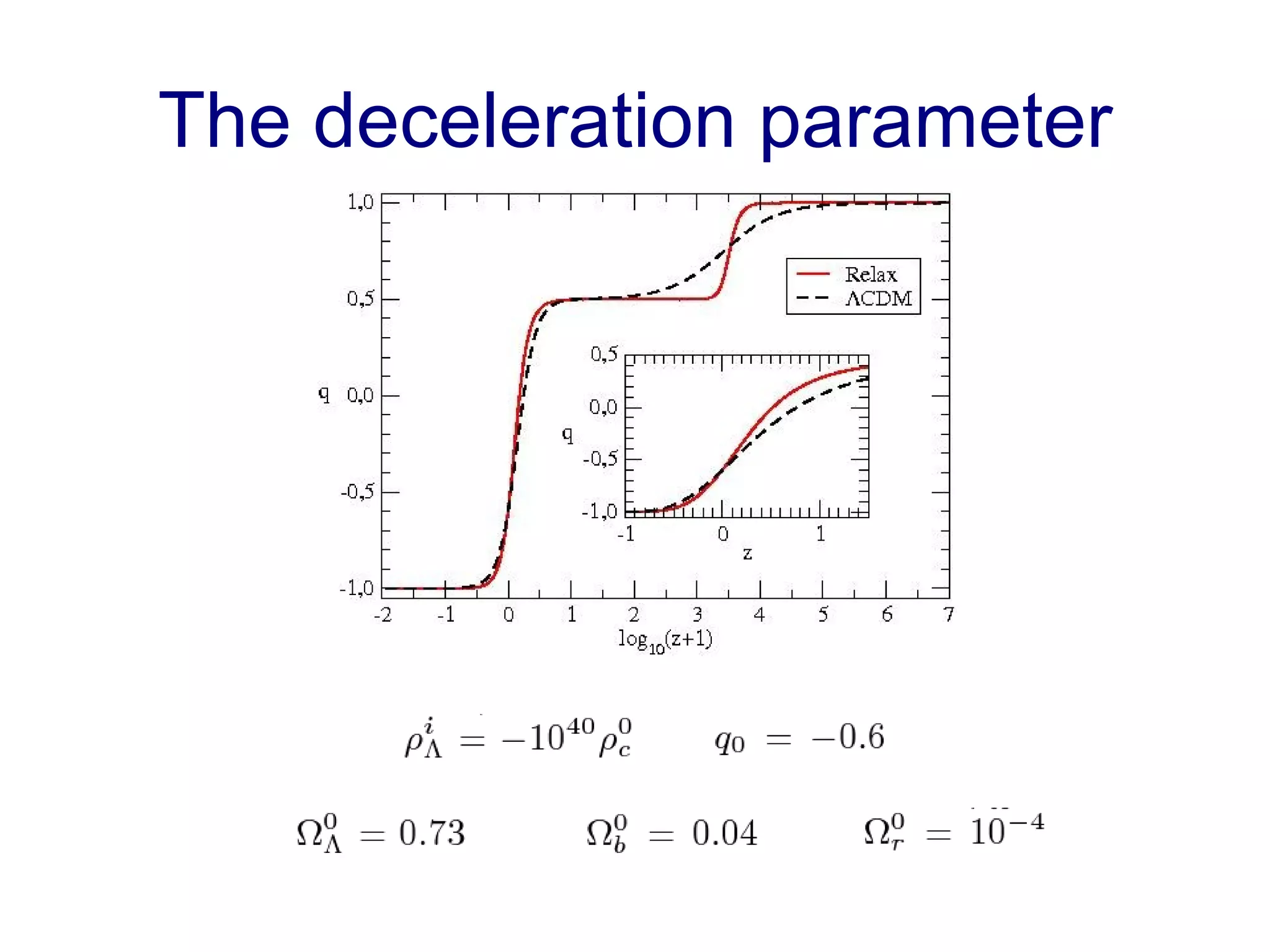
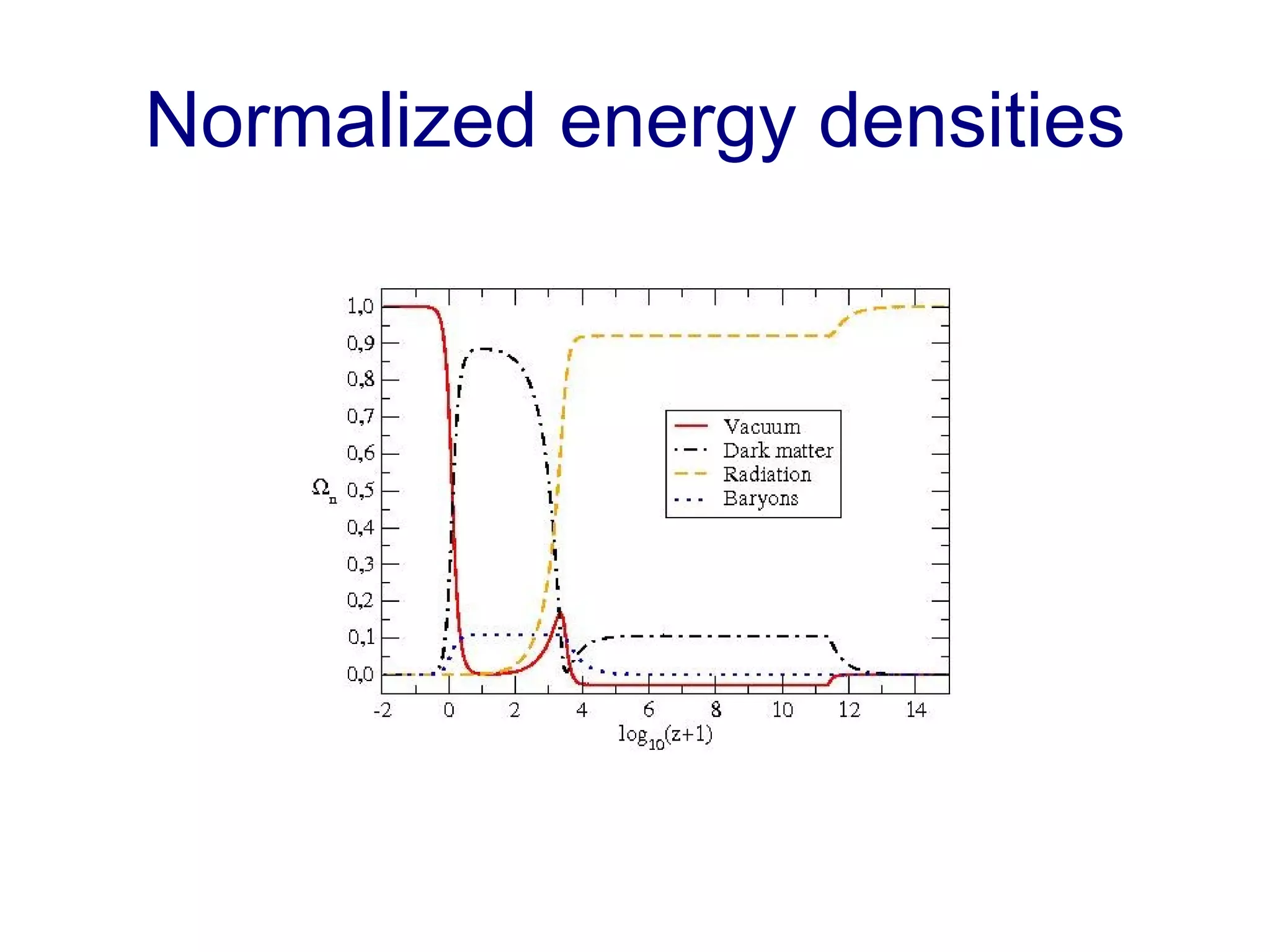
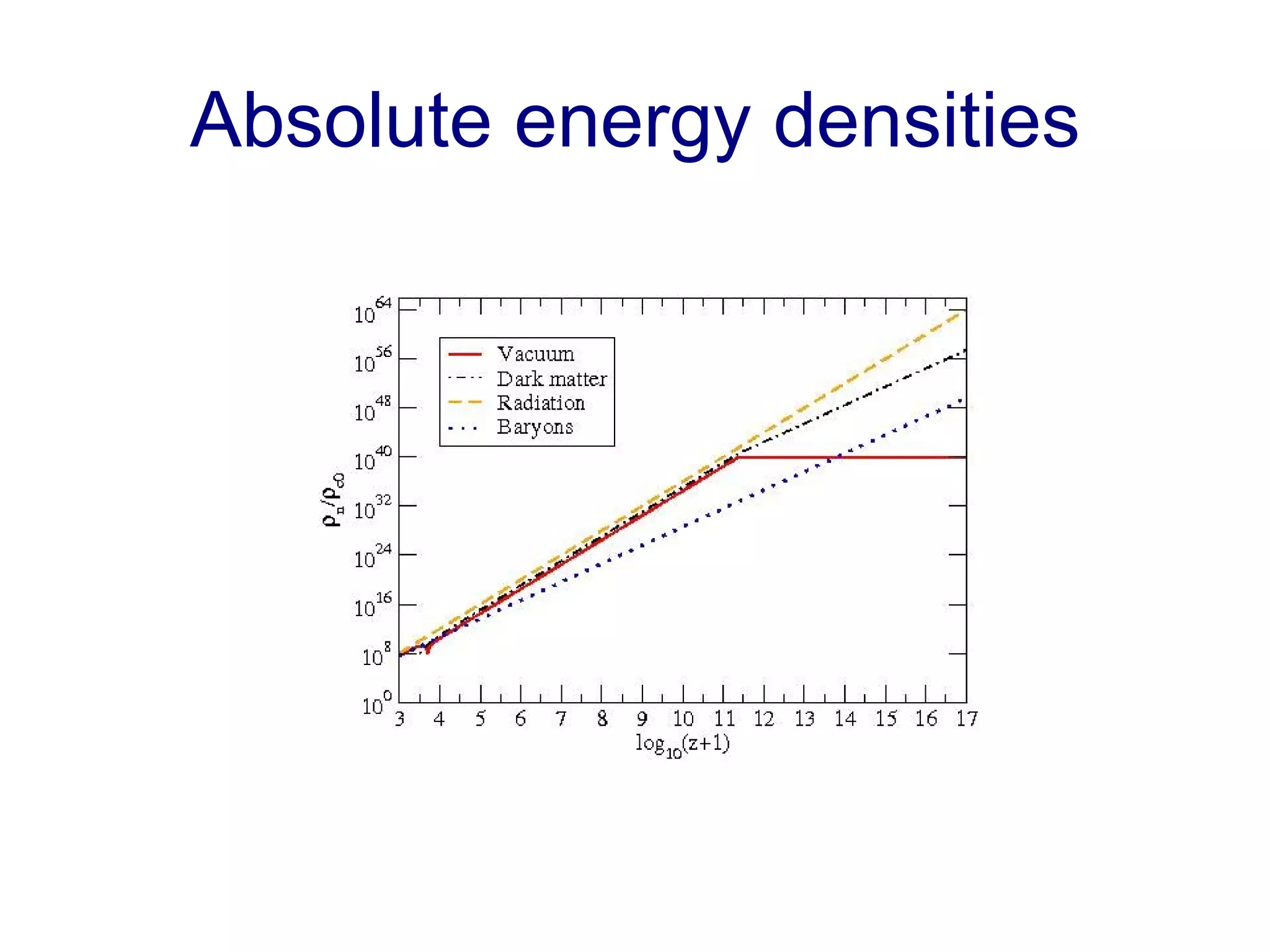
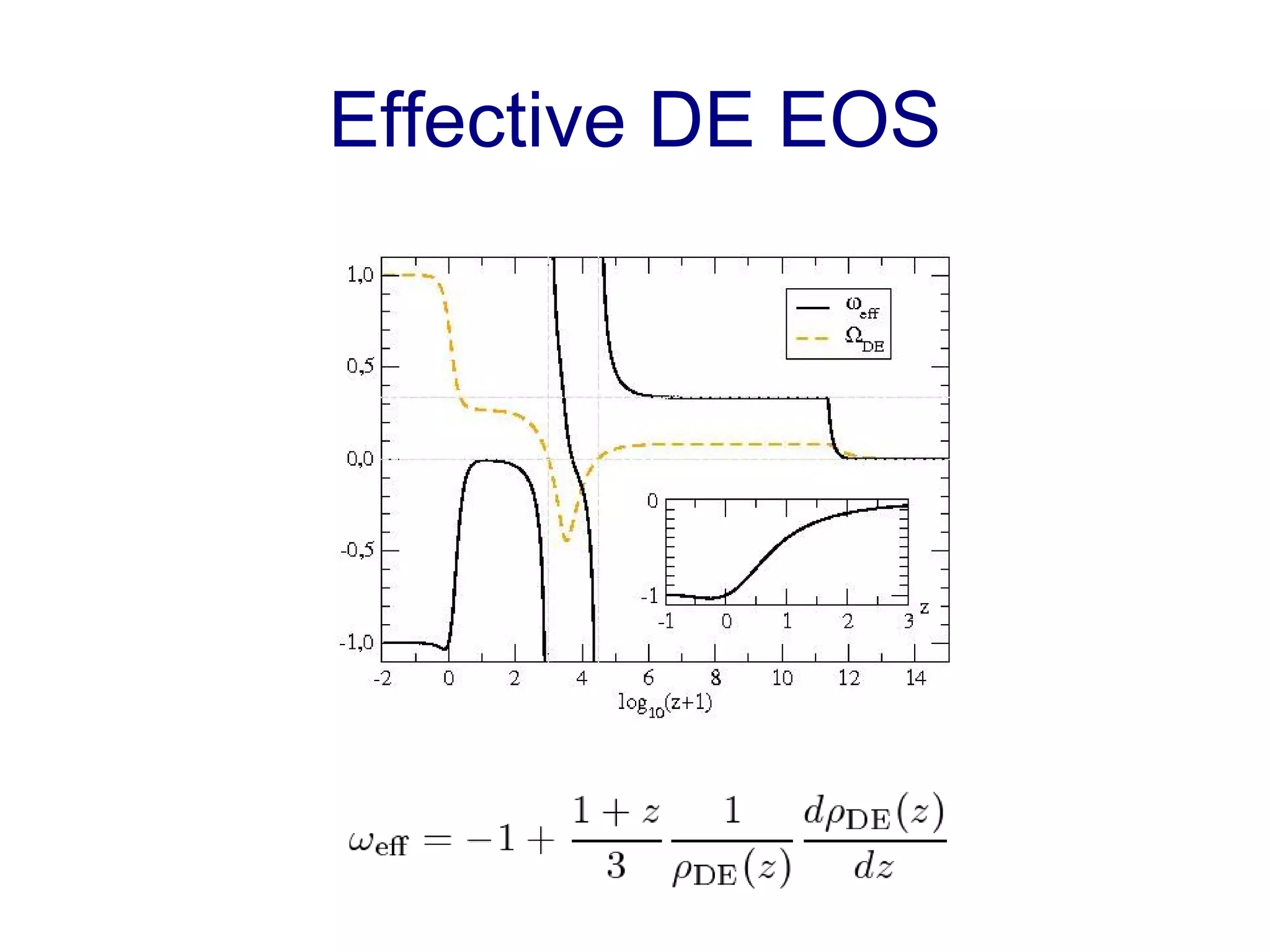
The document discusses the accelerated expansion of the universe and the cosmological constant problem, highlighting observational discoveries and theoretical challenges related to cosmic evolution. It reviews various cosmological models, observations such as supernovae and cosmic microwave background, and different approaches to resolving the cosmological constant problem. The interplay between dark energy, modifications to gravity, and other theoretical frameworks is explored, indicating ongoing debates and the need for precision cosmology to address these complex issues.

1. The accelerated expansion of the universe and the cosmological constant problem Spring Summer School on Strings Cosmology and Particles 31 March – 4 April 2009, Belgrade-Niš, Serbia Hrvoje Štefančić, Theoretical Physics Division, Ruđer Bošković Institute, Zagreb, Croatia

2. Big issues - observational and theoretical Present accelerated expansion of the universe – observational discovery The cosmological constant (vacuum energy) problem – theoretical challenge

3. Our concept of the (present) universe Evolution dominated by gravity the interactions governing the evolution of the universe have to have long range to be effective at cosmological distances matter is neutral at cosmological (and much smaller) scales General relativity Known forms of matter (radiation, nonrelativistic matter) Four dimensional universe

4. The observed universe Isotropic (CMB, averaged galaxy distribution at scales > 50-100 Mpc) Homogeneous – less evidence (indirect) – Copernican principle Homogeneous and isotropic – Cosmological principle Robertson-Walker metric !

5. Expansion of the universe Hubble (1929) – dynamical universe Cosmological redshift Standard forms of matter lead to decelerated expansion Inflation – early epoch of the accelerated expansion 1998 – universe accelerated (decelerated universe expected)

6. FRW model – theoretical description of the expansion Contents: cosmic fluids (general EOS) General relativity in 4D Friedmann equation Continuity equation (Bianchi identity - covariant conservation of energy-momentum tensor) Acceleration

7. FRW model Critical density Omega parameters Cosmic sum rules

8. Cosmological observations – mapping the expansion Standard candles (luminosity distance) Supernovae Ia, GRB Standard rulers CMB (cosmic microwave background) BAO (baryonic acoustic oscillations) Others (gravitational lensing...)

9. Supernovae of the type Ia Standard candles – known luminosity Binary stars – physics of SNIa understood Light curve fitting Luminosity distance – can be determined both observationally and theoretically SNIa dimming – signal of the accelerated expansion

10. Cosmological observations - SNIa http://imagine.gsfc.nasa.gov/docs/science/know_l2/supernovae.html http://www.astro.uiuc.edu/~pmricker/research/type1a/

11. Cosmological observations - CMB http://map.gsfc.nasa.gov/

12. Cosmological observations - LSS structure at cosmological scales (LSS) http://cas.sdss.org/dr5/en/tools/places/

13. Standard cosmological model (up to 1998) Destiny determined by geometry Interplay of spatial curvature and matter content ( Ω m + Ω k =1 ) Even EdS model advocated ( Ω m =1)

14. Spatial curvature COBE – spatial curvature is small. EdS must do the job (models with considerable Ω k are ruled out by the observation of CMB temperature anisotropies

15. SNIa observations (1998) Observations by two teams High z SN Search Team, Riess et al., http://cfa-www.harvard.edu/supernova//home.html Supernova Cosmology Project, Perlmutter et al., http://supernova.lbl.gov/ Λ CDM model – fits the data very well Measurement in the redshift range where the expansion of the universe is really accelerated or there is the transition from decelerated to accelerated expansion – “direct measurement”

16. CMB and BAO Influence to the determination of the acceleration – indirectly CMB – mainly through the distance to the surface of last scattering BAO – similarly

17. Combining observational data Degeneracies of cosmic parameters - different combinations of cosmic parameters may produce the same observed phenomena Removal of degeneracies – using different observations at different redshifts (redshift intervals) SNIa + WMAP + BAO – precision cosmology

18. Observational constraints to the DE EOS E. Komatsu et al., Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation http://arxiv.org/abs/0803.0547

19. Accelerated expansion In a FRW universe the observed signals strongly favor a presently accelerated expansion of the universe (and reject EdS model) Do we interpret the observational data correctly?

20. Classification of theoretical approaches ll R. Bean, S. Caroll, M. Trodden, Insights into dark energy: interplay between theory and observation. Rachel Bean ( Cornell U., Astron. Dept. ) , Sean M. Carroll ( Chicago U., EFI & KICP, Chicago ) , Mark Trodden ( Syracuse U. ) . Oct 2005. 5pp. White paper submitted to Dark Energy Task Force. http://arxiv.org/abs/astro-ph/0510059

21. Distorted signals and unjustified assumptions? Photons from SNIa convert to axions in the intergalactic magnetic field light signal dissipated Reduction in intensity confused for the effects of acceleration C. Csaki, N. Kaloper, J. Terning, Phys. Rev. Lett. 88 (2002) 161302 does not work (very interesting attempt – invokes more or less standard (or at least already known physics) connection with the phantom “mirage”

22. Distorted signals and unjustified assumptions? The influence of inhomogeneities (below 50-100 Mpc) Nonlinearity of GR in its fundamental form Solving Einstein equations in an inhomogeneous universe and averaging the solutions is not equivalent to averaging sources and solving Einsteins equations in a homogeneous universe No additional components (just NR matter) The acceleration is apparent The perceived acceleration begins with the onset of structure formation – very convenient for the cosmic coincidence problem The effect is not sufficient to account for acceleration, but is should be taken into considerations in precise determination of cosmic parameters

23. Distorted signals and unjustified assumptions? Inhomogeneities at scales above the Hubble horizon Underdense region Relinquishing the Copernican principle? Falsifiability? No additional components The effect of “super large scale structure”

24. Mechanism of the acceleration No acceleration in the “old standard cosmological model” Our (pre)concepts of the universe have to be modified Modifying contents – dark energy (+ DM) Modyfing gravity – modified (dark) gravity Modifying dimensionality – new (large) dimesions – braneworld models ... and combinations

25. Dark energy Acceleration by adding a new component – a dark energy component Key property – sufficiently negative pressure Physical realization of a negative pressure? Geometric effect (Lambda from the left side of Einstein eq.) Dynamics of scalar field - domination of potential energy over kinetic energy Corpuscular interpretation – unusual dispersion relation – energy decreasing with the size of momentum

26. Dark energy DE equation of state Dynamics of ρ d in terms of a w > -1: quintessence w = -1: cosmological term w < -1: phantom energy Multiple DE components Crossing of the cosmological constant barrier

27. Dark sector DE interacting with other cosmic components Interaction with dark matter Unification of dark matter and dark energy Chaplygin gas EOS scaling with a

28. DE models Cosmic fluid Scalar fields (quintessence, phantom) ... Effective description of other acceleration mechanisms (at least at the level of global expansion)

29. Λ CDM Benchmark model Only known concepts (CC, NR matter, radiation) small number of parameters The size of Λ not understood – cosmological constant problem(s) Problems with Λ CDM cosmology

30. Quintessence Dynamics of a scalar field in a potential Freezing vs. thawing models “ tracker field” models k-essence (noncanonical kinetic terms)

31. Phantom energy Energy density growing with time Big rip Stability Problems with microscopic formulation Instability to formation of gradients Effective description

32. Singularities New types of singularities Finite time (finite scale factor) singularities Sudden singularities

33. Modified gravity Modification of gravity at cosmological scales Dark gravity (effective dark energy) F(R) gravity – various formulations (metric, Palatini, metric-affine) Conditions for stability Stringent precision tests in Solar system and astrophysical systems

34. Braneworlds Matter confined to a 4D brane Gravity also exists in the bulk Dvali-Gabadadaze-Poratti (DGP) Different DGP models – discussion of the status! Phenomenological modifications of the Friedmann equation – Cardassian expansion

35. The cosmological constant Formally allowed – a part of geometry Introduced by Einstein in 1917 – a needed element for a static universe Pauli – first diagnosis of a problem with zero point energies Identification with vacuum energy – Zeldovich 1967 Frequently used “patch”

36. The expansion with the cosmological constant J. Sol à, hep-ph/0101134v2

37. The expansion with the cosmological constant

38. Contributions to vacuum energy Zero point energies – radiative corrections Bosonic Fermionic Condensates – classical contributions Higgs condensate QCD condensates ...

39. Zero point energies QFT estimates real scalar field spin j

40. Condensates Phase transitions leave contributions to the vacuum energy Higgs potential minimum at contribution to vacuum energy

41. The size of the CC Many disparate contributions Virtually all many orders of magnitude larger than the observed value ZPE - Planck scale “cutoff” ≈ 10 74 GeV 4 ZPE - TeV scale “cutoff” ≈ 10 57 GeV 4 ZPE - Λ QCD scale “cutoff” ≈ 10 -5 GeV 4 Higgs condensate ≈ - 10 8 GeV 4 m electron 4 ≈ 10 -14 GeV 4 The observed value

42. The “old” cosmological constant problem – the problem of size Discrepancy by many orders of magnitude (first noticed by Pauli for the ZPE of the electromagnetic field) Huge fine-tuning implied How huge and of which nature Numerical example: 10 120 1 -0.999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999 = 0.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001 Financial example Instability to variation of a single contribution (parameter)

43. The “old” cosmological constant problem Fundamental theoretical problem – the problem of the vacuum energy density All proposed solutions assume that the “old” CC problem is somehow solved Λ CDM model – CC relaxed to the observed value DE models and other models – CC is zero or much smaller in absolute value compared to the observed DE energy density Even should the future observations confirm the dynamical nature of DE or some other alternative acceleration mechanism, the “old” CC problem must be resolved

44. DE vs CC Raphael Bousso, “TASI lectures on the cosmological constant” “ If a poet sees something that walks like a duck and swims like a duck and quacks like a duck, we will forgive him for entertaining more fanciful possibilities. It could be a unicorn in a duck suit – who's to say! But we know that more likely, it's a duck.” Conditions for a mechanism solving the CC problem

45. Proposed solutions of the “old” CC problem Classification (closely following S. Nobbenhuis, gr-qc/0609011) Symmetry Back-reaction mechanisms Violation of the equivalence principle Statistical approaches

46. Symmetry Supersymmetry Scale invariance Conformal symmetry Imaginary space Energy -> - Energy Antipodal symmetry

47. Back-reaction mechanisms Scalar Gravitons Running CC from Renormalization group Screening caused by trace anomaly

48. Violation of the equivalence principle Non-local Gravity, Massive gravitons Ghost condensation Fat gravitons Composite gravitons as Goldstone bosons

49. Statistical approaches Hawking statistics Wormholes Anthropic Principle

50. The cosmic coincidence problem – the problem of timing Why the CC (DE) energy density and the energy density of (NR) matter are comparable (of the same order of magnitude) at the present epoch? A problem in a DE (CC) approach to the problem of accelerated expansion: DE (CC) energy density scale very differently with the expansion (if presently comparable they were very different in the past and will be very different in the future NR: ρ ~ a -3 DE: ρ ~ a -3(1+w) , slower than a -2 , CC: ~ 1 Also present in many approaches not based on DE

51. Possible solutions of the cosmic coincidence problem Naturally solved in (matter) back-reaction approaches “ tracker field” Oscillating DE model DE-DM interaction models (although problem still present in e.g. Chaplygin gas model) Composite DE model (LambdaXCDM model) Two interacting DE components: a (dynamical) cosmological term and an additional DE component (cosmon X) … .

52. Composite dark energy – Λ XCDM models ordinary matter (radiation and NR matter) separately conserved) Λ XCDM 1 : CT interacting with cosmon J. Grande, J. Sol à , H. Š., JCAP 0608 (2006) 011. Λ XCDM 2 : varaible CT i G, X concerved J. Grande, J. Sol à , H. Š., Phys. Lett . B645 (2007) 236.

53. Ratio of DE and matter energy density

54. Parameter constraints primordial nucelosynthesis: Existence of a stopping point height of the maximum of r :

55. Parameter constraints – cross sections

56. The CC relaxation mechansim Two component model (H.Š. Phys.Lett. B 670 (2009) 246) The inhomogeneous equation of state (S. Nojiri, S.D. Odintsov, Phys. Rev. D 72 (2005) 023003) The continuity equation

57. The model dynamics The dynamics of the Hubble parameter Notation Dynamics in terms of dimensionless parameters with the initial condition H X and a X in principle arbitrary

58. α < −1: the relaxation mechanism for the large cosmological constant The α = −3 case Closed form solution

59. case Late-time symptotic behavior Ʌ eff is small because | Ʌ | is large!

60. Dependence on model parameters

61. Dependence on model parameters

62. Dependence on model parameters

63. Dependence on model parameters

64. case Asymptotic behavior Late-time asymptotic behavior Ʌ eff is small because Ʌ is large!

65. Dependence on model parameters

66. Dependence on model parameters

67. Dependence on model parameters

68. Dependence on model parameters

69. Other parameter regimes For α > −1 the behavior is different The relaxation mechanism is not automatic

70. Fixed points, approach to de Sitter regime general dynamics Fixed point ⇒ Example: ⇒

71. General inhomogeneous EOS dynamics of the scaled Hubble parameter condition for the relaxation mechanism for a small h at late-time

72. Variable cosmological term Running CC Extended running CC Interaction with matter + put β n -> 0 Dynamics of the Hubble parameter

73. Variable cosmological term Late-time asymptotic behavior

74. f(R) modified gravity general dynamics specific example asymptotic de Sitter regime n=1

75. Important questions Abruptness of the transition The onset of the transition The connection to other eras of (accelerated) expansion Addition of other components and other cosmological (RD,MD) eras Cosmological coincidence problem Stability of the mechanism to perturbations Precision tests and the comparisons with the observational data astrophysical scales (e.g. solar system tests) cosmological scales (growth of inhomogeneities)

76. Summary of the relaxation mechanism properties The solution of the CC problem without fine-tuning for both signs of the CC The universe with a large CC has a small positive positive effective CC Ʌ eff is small because | Ʌ| is large Ʌ eff ~ 1/ | Ʌ| candidate physical mechanisms: modified gravity, (nonlinear) viscosity, quantum effects Exchanging “unnatural” parameters for some new (not too complicated) dynamics

77. Relaxing a large cosmological constant - adding matter and radiation F. Bauer, J. Sola, H. Š. arXiv:0902.2215 Components: variable cosmological term (containing a large constant term) dark matter baryons radiation Variable cosmological term and DM interact

78. The formalism The variable cosmological term Constructing f from general coordinate covariant terms Interaction with the DM component

79. ½ Model f=R Radiation domination (controlled by 1-q) transition to de Sitter regime (controlled by small H 2 ) abrupt transition removed RD phase introduced

80. The model Two terms dominated by different values of q and different powers of H Sequence of a RD, MD and de Sitter phases Realistic cosmological model with a relaxed CC

81. The deceleration parameter

82. Normalized energy densities

83. Absolute energy densities

84. Effective DE EOS

85. Conclusions The question of the mechanism of the acceleration of the universe still open The cosmological constant problem(s) – many proposed approaches – decisive arguments still to come The nexus of physics at many very different distance/energy scales Testing ground of the future theoretical, observational and experimental efforts