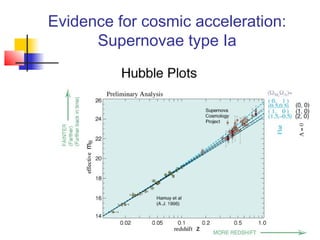
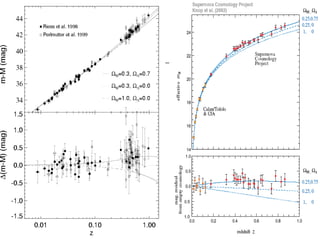
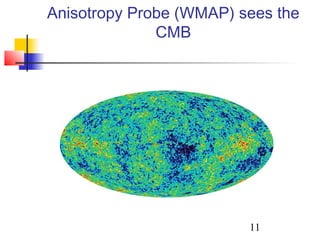
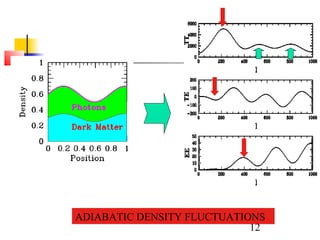
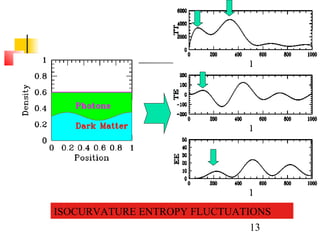
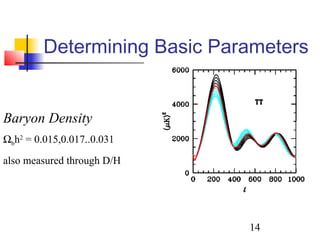
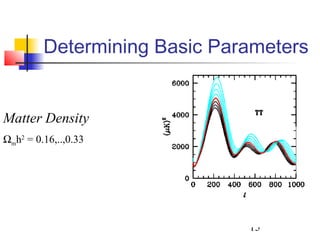
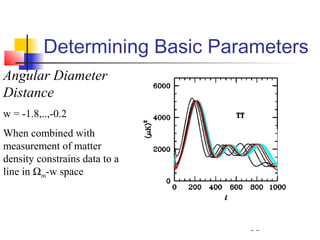
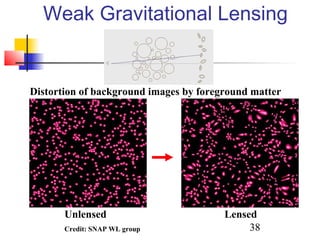
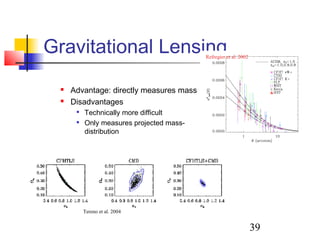
The document discusses the evidence for dark energy from observations of Type Ia supernovae, the cosmic microwave background radiation, and large-scale structure like galaxy clusters. It finds that about 73% of the universe consists of dark energy, which is causing the accelerating expansion of the universe. Future experiments aim to better characterize dark energy and test whether it is due to a cosmological constant, modified gravity, or other explanations like quintessence. Precise measurements of the expansion history and growth of structure can help distinguish between theories of dark energy.

1. 1
What is the Dark Energy?
David Spergel
Princeton University

2. 2
One of the most challenging
problems in Physics
 Several cosmological observations demonstrated
that the expansion of the universe is accelerating
 What is causing this acceleration?
 How can we learn more about this acceleration,
the Dark Energy it implies, and the questions it
raises?

3. 3
Outline
 A brief summary on the contents of the universe
 Evidence for the acceleration and the implied Dark Energy
 Supernovae type Ia observations (SNe Ia)
 Cosmic Microwave Background Radiation (CMB)
 Large-scale structure (LSS) (clusters of galaxies)
 What is the Dark Energy?
 Future Measurements

4. 4
Contents of the universe
(from current observations)
Baryons (4%)
Dark matter (23%)
Dark energy: 73%
Massive neutrinos: 0.1%
Spatial curvature: very close to 0

5. 5
A note on cosmological
parameters
 The properties of the standard cosmological
model are expressed in terms of various
cosmological parameters, for example:
 H0 is the Hubble expansion parameter today
 is the fraction of the matter energy
density in the critical density
(G=c=1 units)
 is the fraction of the Dark Energy
density (here a cosmological constant) in the
critical density
cMM ρρ /≡Ω
π
ρ
8
3 2
H
c ≡
cρρ /ΛΛ ≡Ω

6. 6
Evidence for cosmic acceleration:
Supernovae type Ia

7. 7
Evidence for cosmic acceleration:
Supernovae type Ia
 Standard candles
 Their intrinsic luminosity is know
 Their apparent luminosity can be measured
 The ratio of the two can provide the luminosity-
distance (dL) of the supernova
 The red shift z can be measured independently
from spectroscopy
 Finally, one can obtain dL (z) or equivalently the
magnitude(z) and draw a Hubble diagram

8. 8
Evidence for cosmic acceleration:
Supernovae type Ia

9. 9

10. 10
Evidence from Cosmic Microwave
Background Radiation (CMB)
 CMB is an almost isotropic relic radiation of
T=2.725±0.002 K
 CMB is a strong pillar of the Big Bang
cosmology
 It is a powerful tool to use in order to
constrain several cosmological parameters
 The CMB power spectrum is sensitive to
several cosmological parameters

11. 11
Anisotropy Probe (WMAP) sees the
CMB

12. 12
ADIABATIC DENSITY FLUCTUATIONS

13. 13
ISOCURVATURE ENTROPY FLUCTUATIONS

14. 14
Determining Basic Parameters
Baryon Density
Ωbh2
= 0.015,0.017..0.031
also measured through D/H

15. 15
Determining Basic Parameters
Matter Density
Ωmh2
= 0.16,..,0.33

16. 16
Determining Basic Parameters
Angular Diameter
Distance
w = -1.8,..,-0.2
When combined with
measurement of matter
density constrains data to a
line in Ωm-w space

17. 17
Simple Model Fits CMB data
Readhead et al. astro/ph 0402359

18. 18
Evolution from Initial Conditions IWMAP team
assembled
DA leave
Princeton
WMAP completes
2 year of
observations!
WMAP at Cape

19. 19
Evidence from large-scale structure
in the universe (clusters of galaxies)
 Counting clusters of galaxies can infer the matter energy
density in the universe
 The matter energy density found is usually around ~0.3 the
critical density
 CMB best fit model has a total energy density of ~1, so
another ~0.7 is required but with a different EOS
 The same ~0.7 with a the same different EOS is required
from combining supernovae data and CMB constraints

20. 20
Cosmic
complementarity:
Supernovae,
CMB,
and Clusters

21. 21
What is Dark Energy ?
“ ‘Most embarrassing observation
in physics’ – that’s the only quick
thing I can say about dark energy
that’s also true.”
Edward Witten

22. 22
What is the Dark Energy?
 Cosmological Constant
 Failure of General Relativity
 Quintessence
 Novel Property of Matter

Simon Dedeo astro-ph/0411283

23. 23
 Why is the total value measured from
cosmology so small compared to quantum field
theory calculations of vacuum energy?
 From cosmology: 0.7 critical density ~ 10-48
GeV4
 From QFT estimation at the Electro-Weak (EW)
scales: (100 GeV)4
 At EW scales ~56 orders difference, at Planck
scales ~120 orders
 Is it a fantastic cancellation of a puzzling smallness?
 Why did it become dominant during the “present”
epoch of cosmic evolution? Any earlier, would have
prevented structures to form in the universe (cosmic
coincidence)
COSMOLOGICAL CONSTANT??

24. 24
Anthropic Solution?
 Not useful to discuss creation science
in any of its forms….
Dorothy… we are not in Kansas anymore …

25. 25
Quintessence
 Introduced mostly to address
the “why now?” problem
 Potential determines dark
energy properties (w, sound
speed)
 Scaling models (Wetterich;
Peebles & Ratra)
V(φ) = exp(−φ)
Most of the tracker models
predicted w > -0.7
ρ
matter
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
Zlatev and
Steinhardt
(1999)

26. 26
Current Constraints
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
Seljak et al.
2004
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.

27. 27
Looking for Quintessence
 Deviations from w = -1
 BUT HOW BIG?
 Clustering of dark energy
 Variations in coupling constants (e.g., α)
λφFF/MPL
 Current limits constrain λ < 10-6
If dark energy properties are time dependent, so
are other basic physical parameters

28. 28
Big Bang Cosmology
Homogeneous,
isotropic universe
(flat universe)

29. 29
Rulers and Standard Candles
Luminosity
Distance
Angular
Diameter
Distance

30. 30
Flat M.D. Universe
D = 1500 Mpc for z > 0.5

31. 31
Volume

32. 32
Techniques
 Measure H(z)
 Luminosity Distance (Supernova)
 Angular diameter distance
 Growth rate of structure
.
Checks Einstein equations to first order in perturbation theory

33. 33
What if GR is wrong?
 Friedman equation (measured through
distance) and Growth rate equation are
probing different parts of the theory
 For any distance measurement, there exists a
w(z) that will fit it. However, the theory can
not fit growth rate of structure
 Upcoming measurements can distinguish
Dvali et al. DGP from GR (Ishak, Spergel,
Upadye 2005)

34. 34
Growth Rate of Structure Galaxy Surveys
 Need to measure bias

Non-linear dynamics

Gravitational Lensing

Halo Models

Bias is a function of galaxy properties,
scale, etc….

35. 35
A powerful cosmological probe of Dark Energy:
Gravitational Lensing
Abell 2218: A Galaxy Cluster Lens, Andrew Fruchter et al. (HST)

36. 36
The binding of light

37. 37
Gravitational Lensing by clusters of galaxies
From MPA lensing group

38. 38
Weak Gravitational Lensing
Distortion of background images by foreground matter
Unlensed Lensed
Credit: SNAP WL group

39. 39
Gravitational Lensing
 Advantage: directly measures mass
 Disadvantages

Technically more difficult
 Only measures projected mass-
distribution
Tereno et al. 2004
Refregier et al. 2002

40. 40
Baryon Oscillations
C(θ)
C(θ)
θ
θ
CMB
Galaxy
Survey
Baryon oscillation scale
1o
photo-z slices
Selection
function
Limber Equation
(weaker effect)

41. 41
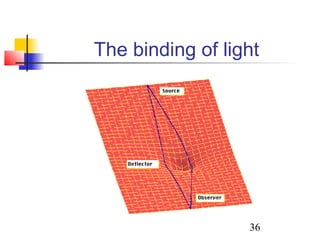
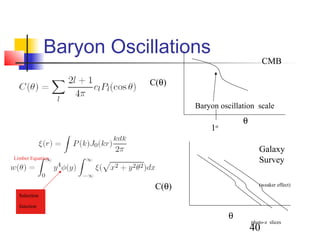
Baryon Oscillations as a
Standard Ruler
 In a redshift survey, we
can measure correlations
along and across the line
of sight.
 Yields H(z) and DA(z)!
[Alcock-Paczynski Effect]
Observer
δr = (c/H)δzδr = DAδθ

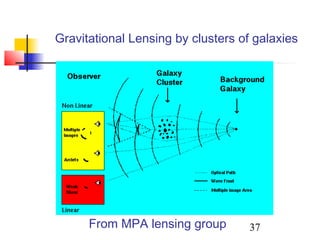
42. 42
Large Galaxy Redshift Surveys
 By performing large spectroscopic surveys, we can measure the
acoustic oscillation standard ruler at a range of redshifts.
 Higher harmonics are at k~0.2h Mpc-1
(λ=30 Mpc).
 Measuring 1% bandpowers in the peaks and troughs requires about 1
Gpc3
of survey volume with number density ~10-3
galaxy Mpc-3
. ~1
million galaxies!
 SDSS Luminous Red Galaxy Survey has done this at z=0.3!
 A number of studies of using this effect
 Blake & Glazebrook (2003), Hu & Haiman (2003), Linder (2003),
Amendola et al. (2004)
 Seo & Eisenstein (2003), ApJ 598, 720 [source of next few figures]

43. 43
Conclusions
 Cosmology provides lots of evidence for
physics beyond the standard model.
 Upcoming observations can test ideas about
the nature of the dark energy.