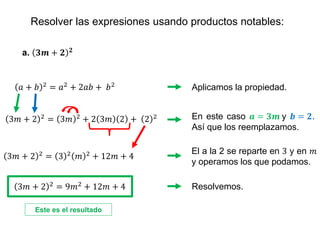
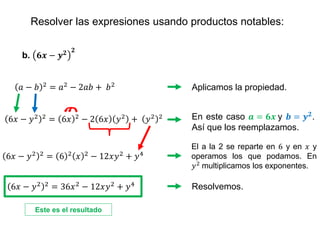
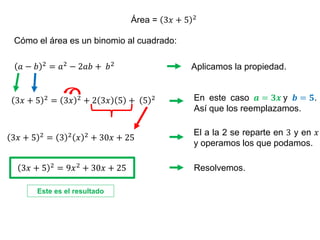
Los productos notables son expresiones algebraicas que provienen de la multiplicación de polinomios, abarcando el cuadrado de binomios, trinomios y la diferencia de cuadrados. Se presentan ejemplos prácticos de cómo aplicar estas propiedades, incluyendo la resolución de expresiones y el cálculo de áreas. Además, se sugieren ejercicios y recursos adicionales para practicar y afianzar conocimientos sobre el tema.

2. PRODUCTOS NOTABLES
Los productos notables son expresiones algebraicas que resultan
de generalizar ciertos casos de multiplicación de polinomios.
Los productos notables que vamos a trabajar en esta guía
son:
1. Cuadrado de un binomio.
2. Cuadrado de un trinomio.
3. Producto de la suma por la diferencia.

3. 1. Cuadrado de un binomio
Cuando se halla el cuadrado de un binomio se deben tener en cuenta
dos casos: el cuadrado de la suma de dos términos y el cuadrado de la
diferencia de dos términos.
𝑎 + 𝑏 2 = 𝑎2 + 2𝑎𝑏 + 𝑏2
El cuadrado de la SUMA de dos términos es igual al cuadrado del
primer término, más el doble del producto del primer término por el
segundo término, más el cuadrado del segundo término:
Recordemos que:
Binomio es que tiene dos término.
𝑎 y 𝑏 pueden ser cualquier variable (letra) o constante (número)

4. 1. Cuadrado de un binomio
𝑎 − 𝑏 2
= 𝑎2
− 2𝑎𝑏 + 𝑏2
El cuadrado de la DIFERENCIA de dos términos es igual al cuadrado
del primer término, menos el doble producto del primer término por el
segundo término, más el cuadrado del segundo término:
Recordemos que:
Binomio es que tiene dos término.
𝑎 y 𝑏 pueden ser cualquier variable (letra) o constante (número)

5. EJEMPLO 1

6. Resolver las expresiones usando productos notables:
a. 𝟑𝒎 + 𝟐 𝟐
Aplicamos la propiedad.
𝑎 + 𝑏 2 = 𝑎2 + 2𝑎𝑏 + 𝑏2
En este caso 𝒂 = 𝟑𝒎 y 𝒃 = 𝟐.
Así que los reemplazamos.
El a la 2 se reparte en 3 y en 𝑚
y operamos los que podamos.
3𝑚 + 2 2 = 3 2 𝑚 2 + 12𝑚 + 4
Resolvemos.
3𝑚 + 2 2 = 3𝑚 2 + 2 3𝑚 2 + 2 2
3𝑚 + 2 2
= 9𝑚2
+ 12𝑚 + 4
Este es el resultado

7. EJEMPLO 2

8. Resolver las expresiones usando productos notables:
b. 𝟔𝒙 − 𝒚𝟐 𝟐
Aplicamos la propiedad.
𝑎 − 𝑏 2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
En este caso 𝒂 = 𝟔𝒙 y 𝒃 = 𝒚𝟐.
Así que los reemplazamos.
El a la 2 se reparte en 6 y en 𝑥 y
operamos los que podamos. En
𝑦2
multiplicamos los exponentes.
6𝑥 − 𝑦2 2 = 6 2 𝑥 2 − 12𝑥𝑦2 + 𝑦4
Resolvemos.
6𝑥 − 𝑦2 2 = 6𝑥 2 − 2 6𝑥 𝑦2 + 𝑦2 2
6𝑥 − 𝑦2 2
= 36𝑥2
− 12𝑥𝑦2
+ 𝑦4
Este es el resultado

9. EJEMPLO 3

10. Hallar el área que se ilustra en el cuadrado de la figura:
Recordemos que el área es:
A = base x altura
Identifiquemos qué tenemos:
Base: 3𝑥 + 5 Altura: 3𝑥 + 5
Reemplazamos la base y la altura
Área = 3𝑥 + 5 3𝑥 + 5
Área = 3𝑥 + 5 2
Como los dos binomios son iguales lo podemos escribir como:

11. Aplicamos la propiedad.
𝑎 − 𝑏 2 = 𝑎2 − 2𝑎𝑏 + 𝑏2
Área = 3𝑥 + 5 2
Cómo el área es un binomio al cuadrado:
En este caso 𝒂 = 𝟑𝒙 y 𝒃 = 𝟓.
Así que los reemplazamos.
El a la 2 se reparte en 3 y en 𝑥
y operamos los que podamos.
3𝑥 + 5 2 = 3 2 𝑥 2 + 30𝑥 + 25
Resolvemos.
3𝑥 + 5 2 = 3𝑥 2 + 2 3𝑥 5 + 5 2
3𝑥 + 5 2
= 9𝑥2
+ 30𝑥 + 25
Este es el resultado

12. 2. Cuadrado de un trinomio
El cuadrado de la suma de tres términos es igual al cuadrado del
primer término, más el cuadrado del segundo término, más el cuadrado
del tercer término, más el doble producto del primer término por el
segundo término, más el doble producto del segundo término por el
tercer término, más el doble producto del primer término por el tercer
término.
𝑎 + 𝑏 + 𝑐 2
= 𝑎2
+ 𝑏2
+ 𝑐2
+ 2𝑎𝑏 + 2𝑏𝑐 + 2𝑎𝑐

13. Cuando tengamos un número negativo en alguno de los tres
términos. Ese menos solo afectará a los números que tengan esa
variable. No a los que tengan el exponente 2. Es decir:
𝑎 − 𝑏 + 𝑐 2
= 𝑎2
+ 𝑏2
+ 𝑐2
− 2𝑎𝑏 − 2𝑏𝑐 + 2𝑎𝑐
𝑎 + 𝑏 − 𝑐 2 = 𝑎2 + 𝑏2 + 𝑐2 + 2𝑎𝑏 − 2𝑏𝑐 − 2𝑎𝑐
𝑎 − 𝑏 − 𝑐 2
= 𝑎2
+ 𝑏2
+ 𝑐2
− 2𝑎𝑏 + 2𝑏𝑐 − 2𝑎𝑐

14. EJEMPLO 1

15. Halla el resultado de la siguiente expresión aplicando
productos notables:
𝟐𝒑 + 𝟑𝒒 − 𝒓𝟐 𝟐
Aplicamos la propiedad.
En este caso 𝒂 = 𝟐𝒑, 𝒃 = 𝟑𝒑 y 𝒄 = 𝒓𝟐
así que los reemplazamos.
2𝑝 + 3𝑞 − 𝑟2 2 = 2𝑝 2 + 3𝑞 2 + 𝑟2 2 + 2 2𝑝 3𝑞 − 2 3𝑞 𝑟2 − 2 2𝑝 𝑟2
𝑎 + 𝑏 − 𝑐 2
= 𝑎2
+ 𝑏2
+ 𝑐2
+ 2𝑎𝑏 − 2𝑏𝑐 − 2𝑎𝑐
2𝑝 + 3𝑞 − 𝑟2 2
= 2𝑝 2
+ 3𝑞 2
+ 𝑟2 2
+ 2 2𝑝 3𝑞 − 2 3𝑞 𝑟2
− 2 2𝑝 𝑟2
2𝑝 + 3𝑞 − 𝑟2 2
= 4𝑝2
+ 9𝑞2
+ 𝑟4
+ 12𝑝𝑞 − 6𝑞𝑟2
− 4𝑝𝑟2
Este es el resultado

16. 3. Producto de la suma por la diferencia
La suma por la diferencia de dos términos es igual a la diferencia de
los cuadrados de dichos términos:
𝑎 + 𝑏 𝑎 − 𝑏 = 𝑎2 − 𝑏2
Este caso es para cuando tenemos dos paréntesis con los mismos
términos pero con un signo diferente.

17. EJEMPLO 1

18. Halla el resultado de la siguiente expresión aplicando
productos notables:
𝟒𝒚𝟐 − 𝒛𝟐 𝟒𝒚𝟐 − 𝒛𝟐
Aplicamos la propiedad.
En este caso 𝒂 = 𝟒 𝒚𝟐
y 𝒃 = 𝒛𝟐
así
que los reemplazamos.
4𝑦2
− 𝑧2
4𝑦2
+ 𝑧2
= 4𝑦2 2
− 𝑧2 2
𝑎 + 𝑏 𝑎 − 𝑏 = 𝑎2 − 𝑏2
4𝑦2 − 𝑧2 4𝑦2 + 𝑧2 = 16𝑦4 − 𝑧4
Este es el resultado
Repartimos el exponente para cada
término y solucionamos.

19. Ejercicios # 1
Van a realizar los siguientes ejercicios.
Resuélvanlos y al final de la diapositiva está el
resultado para que los comparen.
Resolver los siguientes productos notables:
1. 2𝑥 + 𝑦 2
2. 7𝑥3𝑦 − 4 2
3. 𝑚𝑛4 + 𝑛 2
4. 𝑚 + 3𝑛2 + 4 2
5. 2𝑥2 + 3𝑦3 2𝑥2 − 3𝑦3
6. 𝑥2𝑦3 − 4𝑧2 𝑥2𝑦3 + 4𝑧2
7.
1
2
𝑥2 + 3𝑦2 − 𝑐2
2

20. LIBRO SANTILLANA
En el libro Santillana Vol. 1 pág. 92, 93, 95 y 96 podemos
encontrar la definición y ejemplos de binomio al cuadrado,
trinomio al cuadrado y producto de la suma por la diferencia.
En el libro Santillana Vol. 1 pág. 94, 96 y 97 podemos encontrar
ejercicios de binomio al cuadrado, trinomio al cuadrado y
producto de la suma por la diferencia. Con estos ejercicios
puedes practicar y afianzar tus conocimientos.

21. LIBRO SANTILLANA
Les sugiero que realizan los puntos 209 al 218 y el punto 224 de la pág.
94; los puntos 241 al 247 y el punto 253 de la pág. 97. Cuando tengan
el resultado me pueden enviar una foto sólo del resultado y yo les
confirmo si está bien o no.
En la plataforma Santillana Compartir podrán encontrar ejemplos o
actividades didácticas.
Visita el E-book – unidad 2 – pág. 92 busca este icono
encontraras un video explicativo acerca de binomio al cuadrado. Y en la
pág. 96 encontrar estos iconos los cuales nos muestran un
video explicativo acerca del producto de la suma por la diferencia y un
taller con puntos diferentes.

22. Si quieren ver más ejercicios y ejemplos…
pueden visitar mi Instagram o pagina web, en
las cuales constantemente estaré publicando
contenido matemático.
https://www.instagram.com/joselprofe/
https://mathpage.wixsite.com/joselprofe

23. Pueden visitar los siguientes Links para ver más
ejemplos y explicación acerca de productos
notables.
https://www.youtube.com/watch?v=zmz0RjoIl0Y
https://www.youtube.com/watch?v=ubj9qS69cwY
Binomio al cuadrado o cuadrado de un binomio
https://www.youtube.com/watch?v=o6PkQJEQql4

24. Pueden visitar los siguientes Links para ver más
ejemplos y explicación acerca de productos
notables.
https://www.youtube.com/watch?v=BtTF7NrhmOM
https://www.youtube.com/watch?v=HaLw4Kae5QY
Trinomio al cuadrado
https://www.youtube.com/watch?v=YQx4QwzDosI

25. Pueden visitar los siguientes Links para ver más
ejemplos y explicación acerca de productos
notables.
https://www.youtube.com/watch?v=NrHAZ8q6_mY
https://www.youtube.com/watch?v=dm4c95Mjj6E
Producto de la suma por la diferencia
https://www.youtube.com/watch?v=xH0d1suuYsM

26. Solución de ejercicios # 1
1. 4𝑥2 + 4𝑥𝑦 + 𝑦2
2. 49𝑥6𝑦2 − 56𝑥3𝑦 + 16
3. 𝑚2𝑛8 + 2𝑚𝑛5 + 𝑛2
4. 𝑚2 + 9𝑛4 + 16 + 6𝑚𝑛2 + 24𝑛2 + 8𝑚
5. 4𝑥4 − 9𝑦6
6. 𝑥4𝑦6 − 16𝑧4
7.
1
4
𝑥4 + 9𝑦4 + 𝑐4 + 3𝑥2𝑦2 − 6𝑦2𝑐2 − 𝑥2𝑐2

27. ¡GRACIAS!