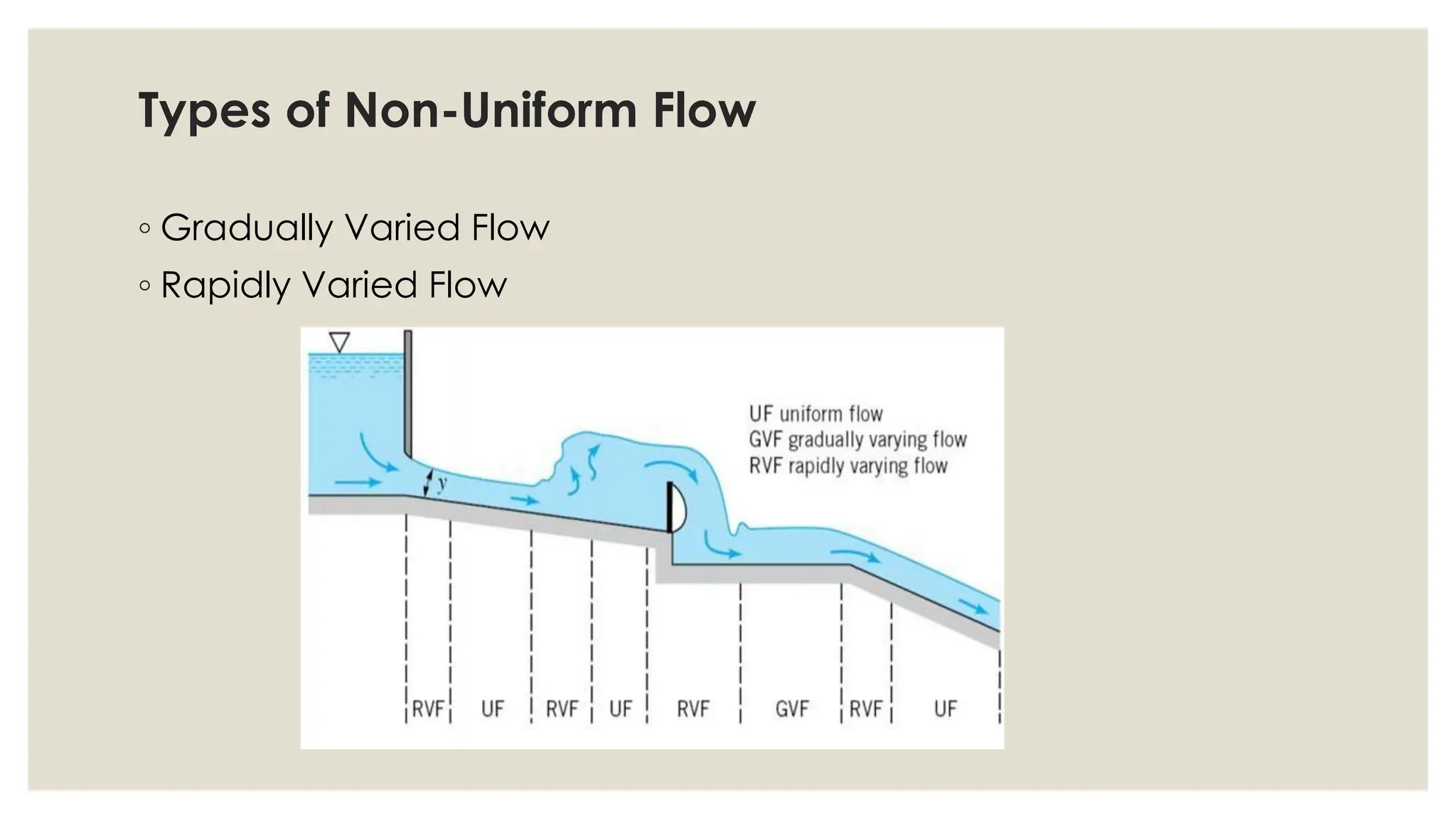
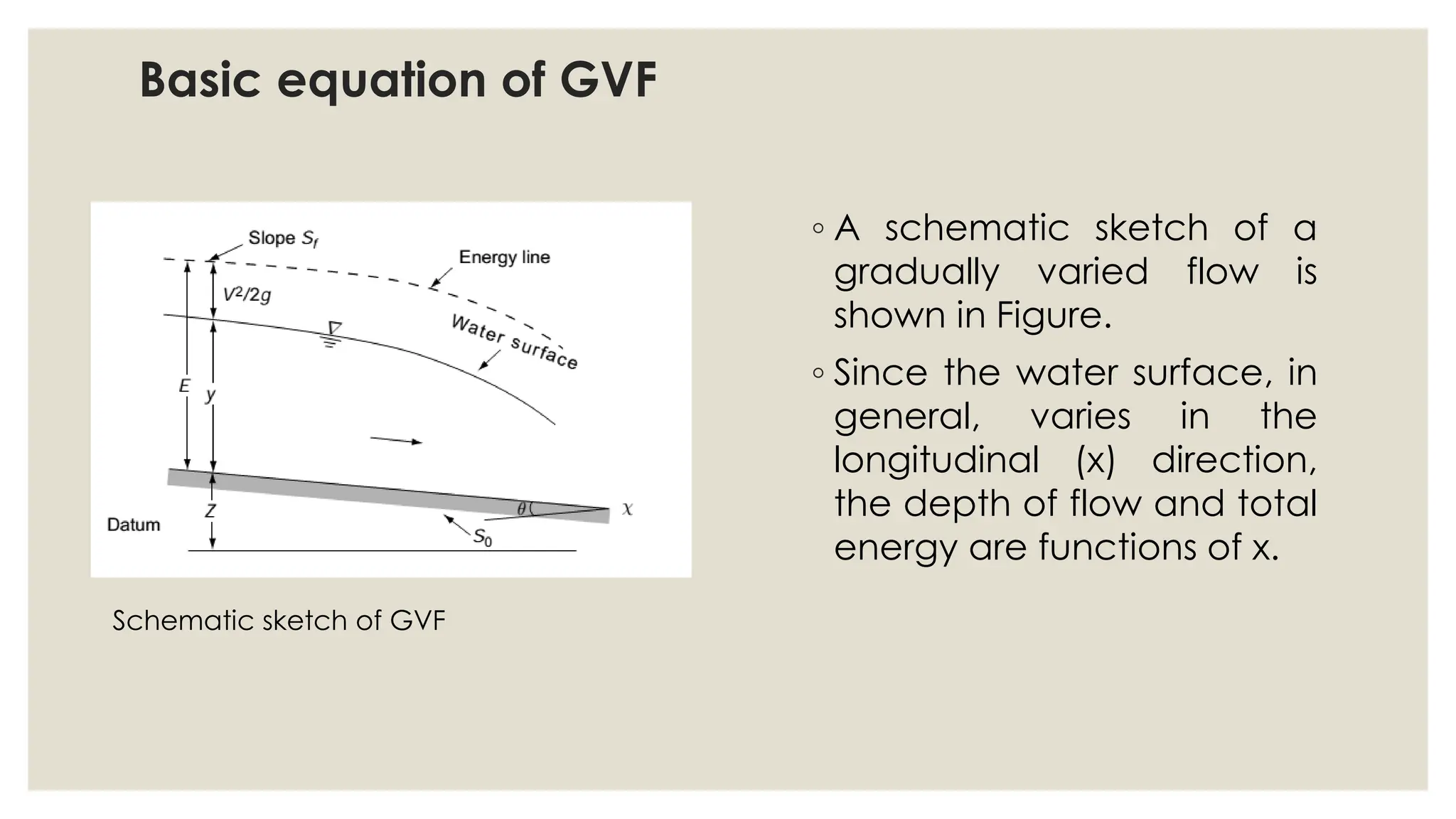
This document discusses gradually varied flow in open channels. It defines gradually varied flow and rapid flow, and lists some common causes of gradually varied flow including changes in channel shape, slope, obstructions, and frictional forces. It also lists the assumptions of gradually varied flow models including prismatic channels, constant Manning's n, hydrostatic pressure, and fixed velocity distribution. The basic differential equation for gradually varied flow relates the water surface slope, energy slope, channel bed slope, discharge, conveyance, and hydraulic radius. Channel bed slopes are also classified.

1. UNIT 5: GRADUALLY VARIED FLOW
AND RAPIDLY VARIED FLOW

2. Types of Non-Uniform Flow
◦ Gradually Varied Flow
◦ Rapidly Varied Flow

3. Occurrence of GVF
◦ The GVF may be caused because of one of the reasons
◦ Change in shape and size of cross section
◦ Change in slope of channel
◦ Presence of obstruction (Weir etc)
◦ Change in frictional forces at boundary
◦ Examples: Flow upstream of weir of dam, flow below sluice gate etc.

4. Assumptions in GVF
1. The channel is prismatic.
2. Energy slope is computed by uniform flow formula, i.e. Manning’s or Chezy’s formula.
3. Bottom slope of the channel (θ) is very small, therefore, the depth measured
perpendicular to the bed and along a vertical are same.
4. The pressure distribution is hydrostatic; and the pressure correction factor is taken
as unity.
5. Velocity distribution in the channel section is fixed; therefore, the energy and
momentum correction factor, i.e., ‘α’ and ‘β’ remain constant in the channel reach.
6. The channel is prismatic, i.e., the channel has a constant slope and its shape remains
same over the reach of the channel under consideration.
7. Roughness coefficient of the channel is constant throughout.

5. Uniform flow in open channel
◦ If the flow in open channel is considered to be uniform, the the
Manning’s equation will be
2
2/3
n
f
V
S
R
 
=  
 
◦ If the flow in open channel is considered to be uniform, the the
Chezy’s equation will be
2
f
V
S
C R
 
=  
 

6. Basic equation of GVF
◦ A schematic sketch of a
gradually varied flow is
shown in Figure.
◦ Since the water surface, in
general, varies in the
longitudinal (x) direction,
the depth of flow and total
energy are functions of x.
Schematic sketch of GVF

7. ◦ Consider the total energy H of a gradually varied fl ow in a
channel of small slope and  = 1.0 as
( )
( )
2
2
2
2
since, P=0,
2
(1)
2
P V
H z y
g
V
H z y
g
V
H z E E y
g

= + + +
= + +
 
= + = +
 
 
Differentiating this equation (1) w.r.t. to x,
dH dZ dE
dx dx dx
= +
2
(2)
2
dH dZ dy d V
dx dx dx dx g
 
= + +  
 
Basic equation of GVF

8. ◦ (dH/dx) represents the energy slope. Since the total energy of the flow always
decreases in the direction of motion, it is common to consider the slope of the
decreasing energy line as positive.
◦ It is denoted by Sf.
2
(2)
2
dH dZ dy d V
dx dx dx dx g
 
= + +  
 
In Equation (2),
f
dH
S
dx
= −
◦ (dz/dx) denotes the bottom slope. It is common to consider the channel slope with bed
elevations decreasing in the downstream direction as positive. It is
◦ Denoted as S0
0
dz
S
dx
= −
◦ (dy/dx) represents the water surface slope relative to the bottom of the channel.
Basic equation of GVF

9. 2 2 2
2 3
2 2
d V d Q dy Q dy
dx g dy gA dx gA dx
   
= = −
   
   
Since,
dA
T
dy
=
2 2
3
2
d V Q T dy
dx g gA dx
 
= −
 
 
Substituting in Equation (2),
2
0 3
f
dy Q T dy
S S
dx gA dx
 
− = − + − 
 
Rearranging the terms,
0
2
3
(3)
1
f
S S
dy
dx Q T
gA
−
=
 
−  
 
Equation (3) is known as ‘Basic differential equation of GVF’ or ‘Dynamic equation of GVF’
Basic equation of GVF

10. Other forms of GVF
◦ If K = conveyance at any depth y and K0 = conveyance
corresponding to the normal depth y0, then
f
Q
K
S
= Basic assumption of GVF
◦ For uniform flow,
0
o
Q
K
S
=
2
0
2
0
f
S K
S K
=

11. ◦ Similarly, if Z = section factor at depth y and Zc = section factor at
the critical depth yc,
3
2 A
Z
T
=
◦ For uniform flow,
3
2 c
c
c
A
Z
T
=
2
2
3 2
c
z
Q T
gA z
=
Other forms of GVF

12. 0 2
3
1
1
f
S
dy
S
dx Q T
gA
−
=
 
− 
 
2
0
0 2
1
1 c
K
dy K
S
dx z
z
 
− 
 
=
 
− 
 
Other forms of GVF

13. Classification of channel bottom slope
◦ Critical slope: The channel bottom slope is designated as critical when
bottom slope (S0) is equal to critical slope (Sc). S0 = Sc, yn = yc
◦ Mild slope: The channel bottom slope is designated as mild when bottom
slope (S0) is less than critical slope (Sc). S0 < Sc, yn > yc
◦ Steep Slope: The channel bottom slope is designated as steep when,
when bottom slope (S0) is greaterthan critical slope (Sc). S0 > Sc, yn < yc
◦ Horizontal slope: When channel bottom slope is equal to zero. S0 = 0, yn =

◦ Adverse slope: When the channel bottom instead f falling rises in the
direction of flow, it is designated as adverse slope. S0 <0, yn is imaginary