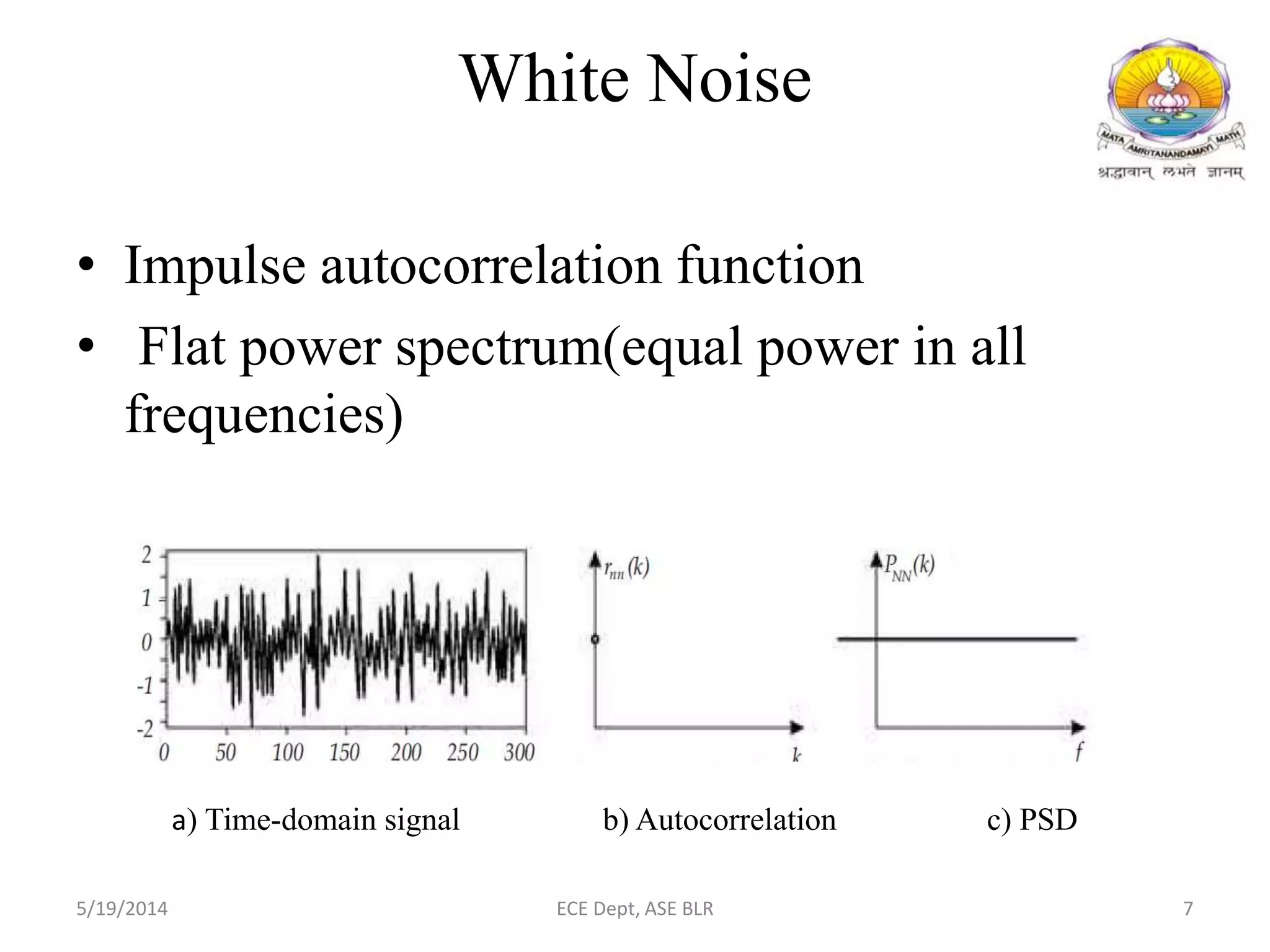
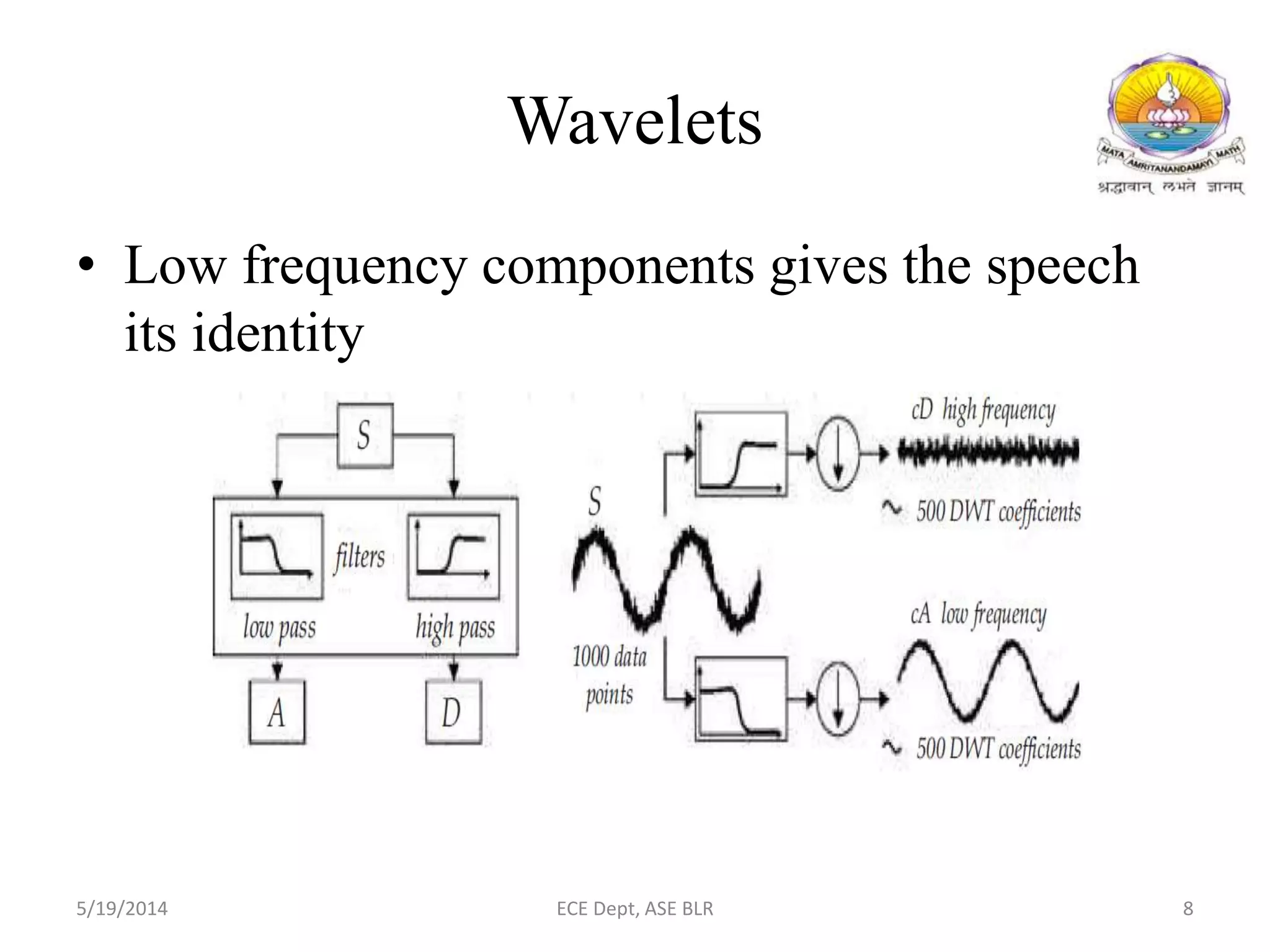
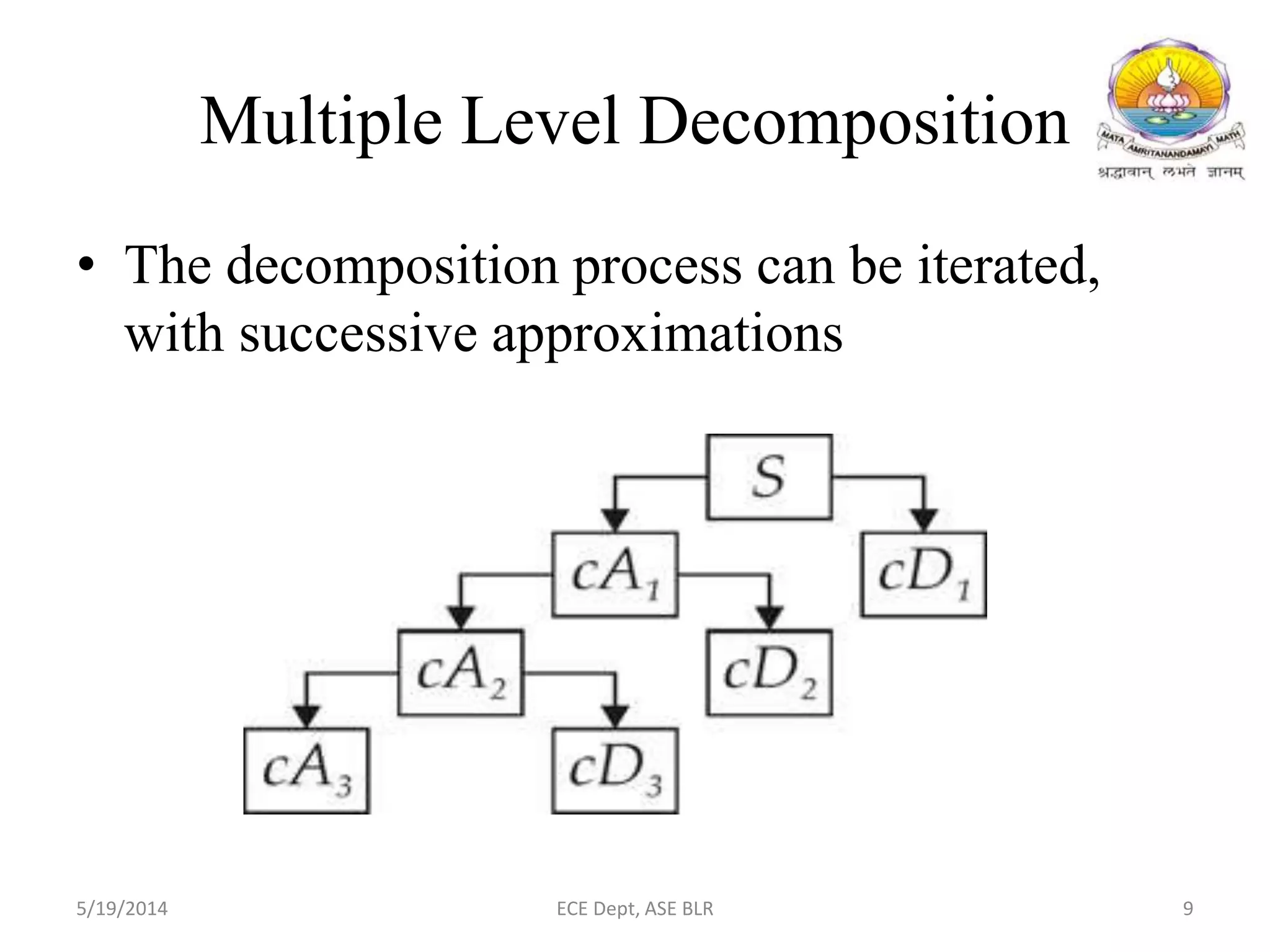
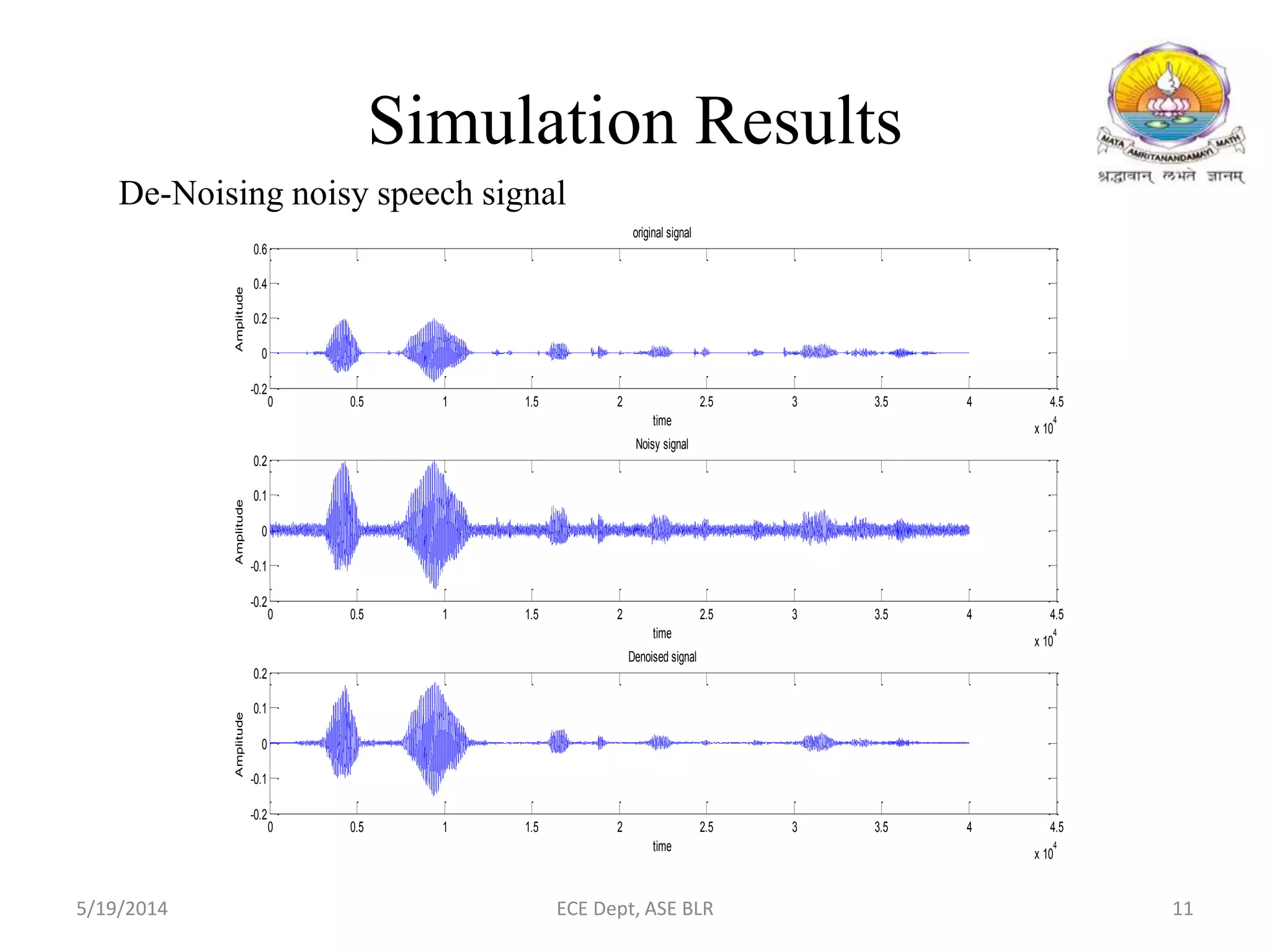
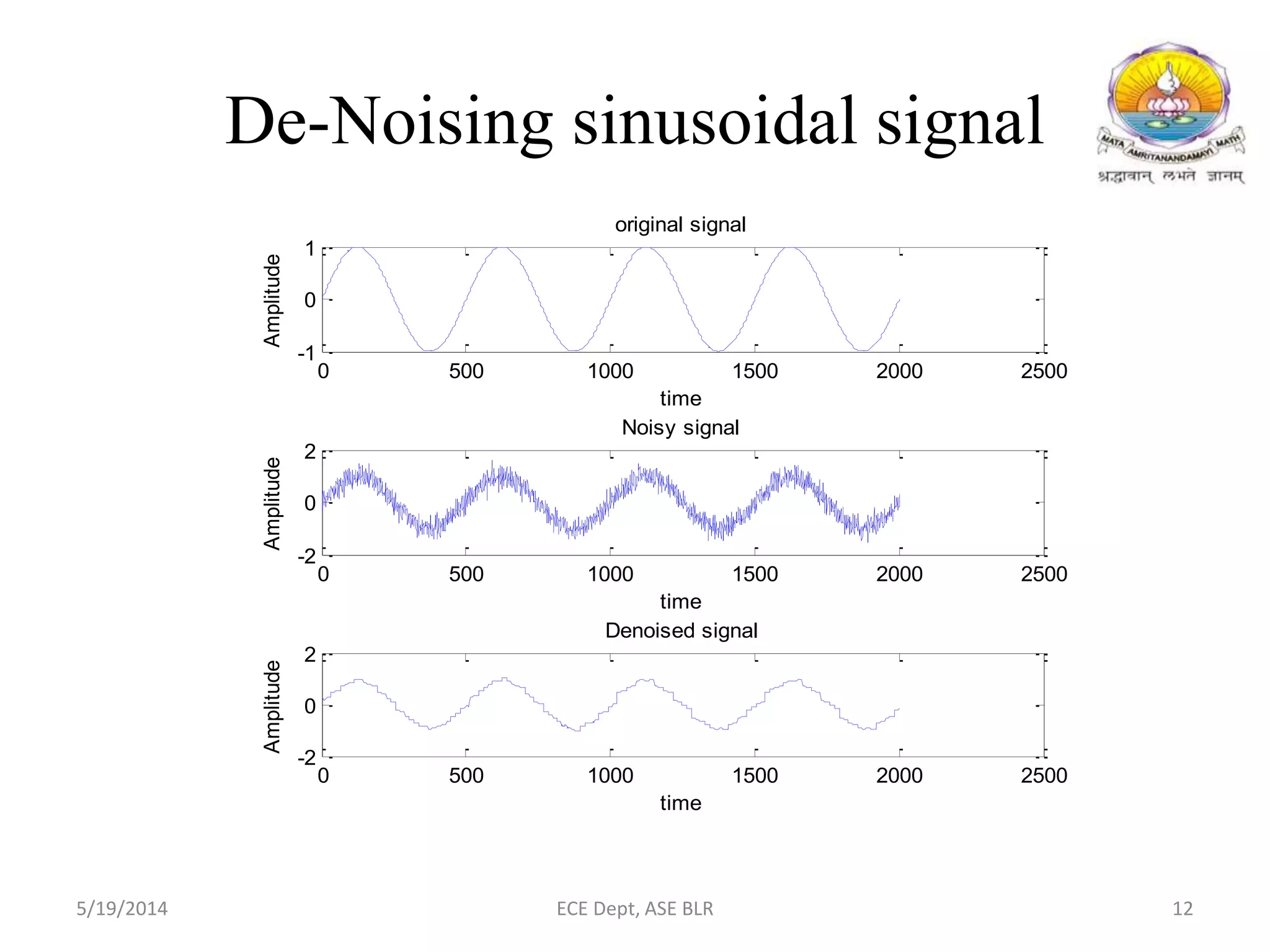
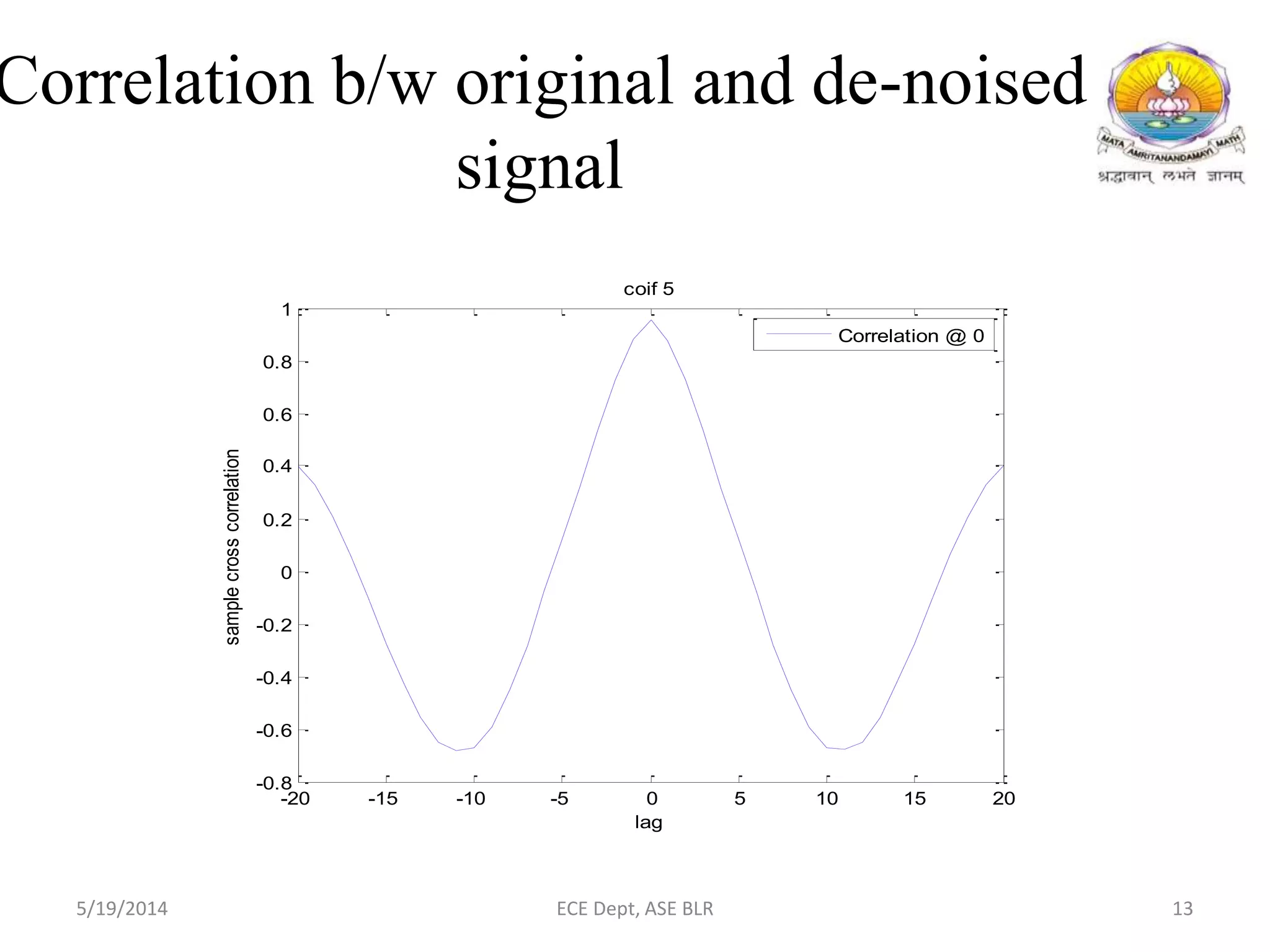
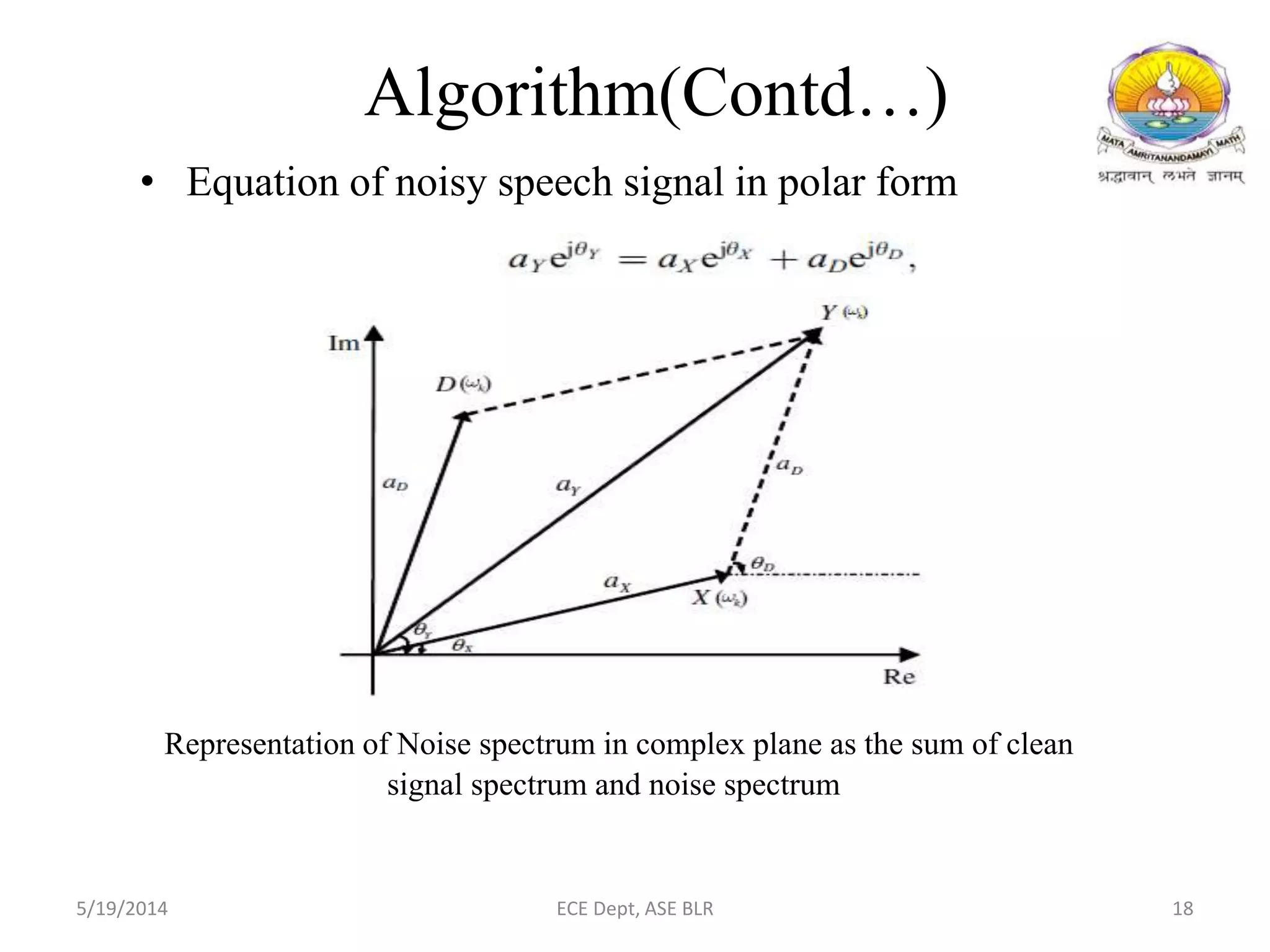
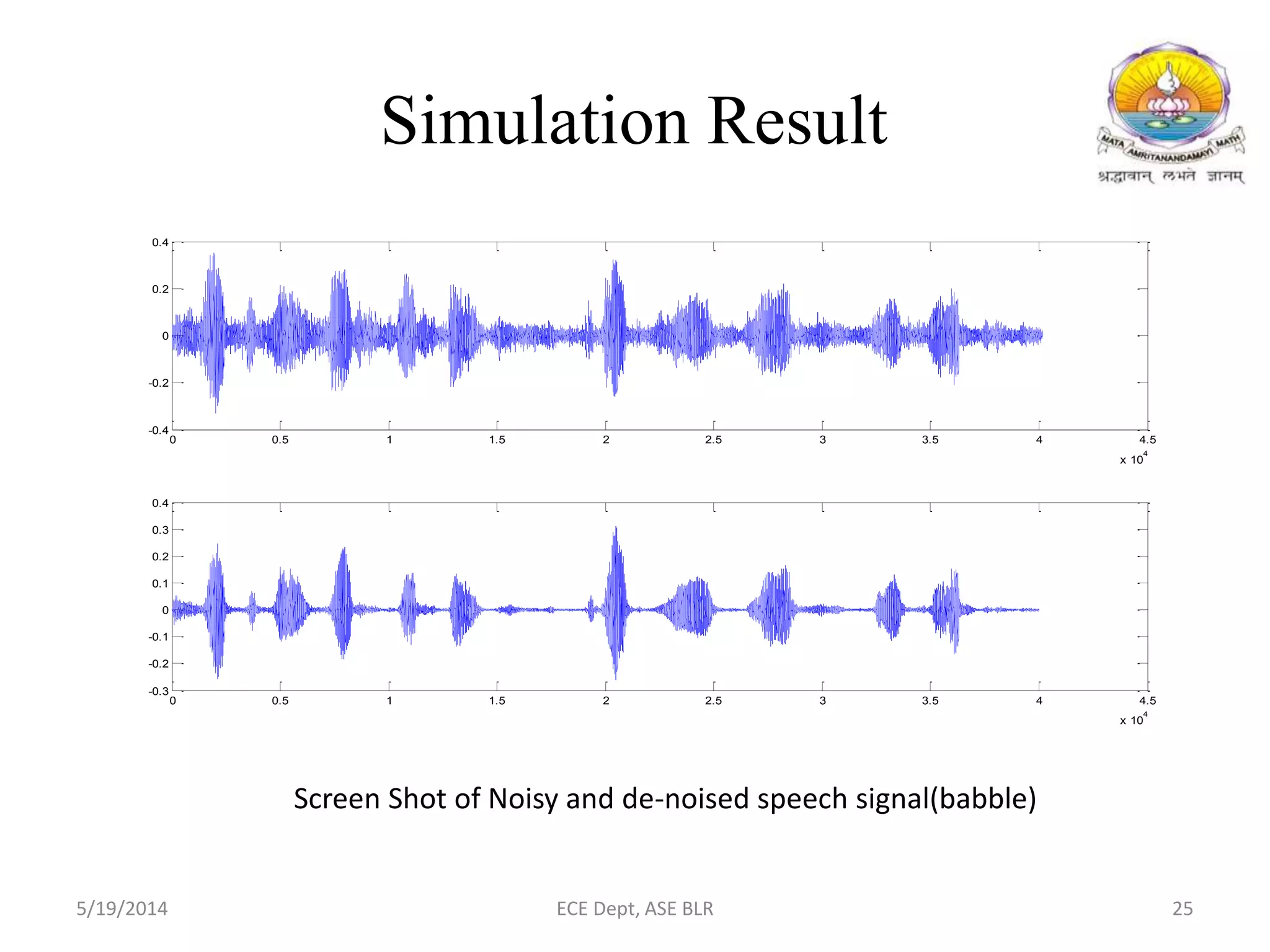
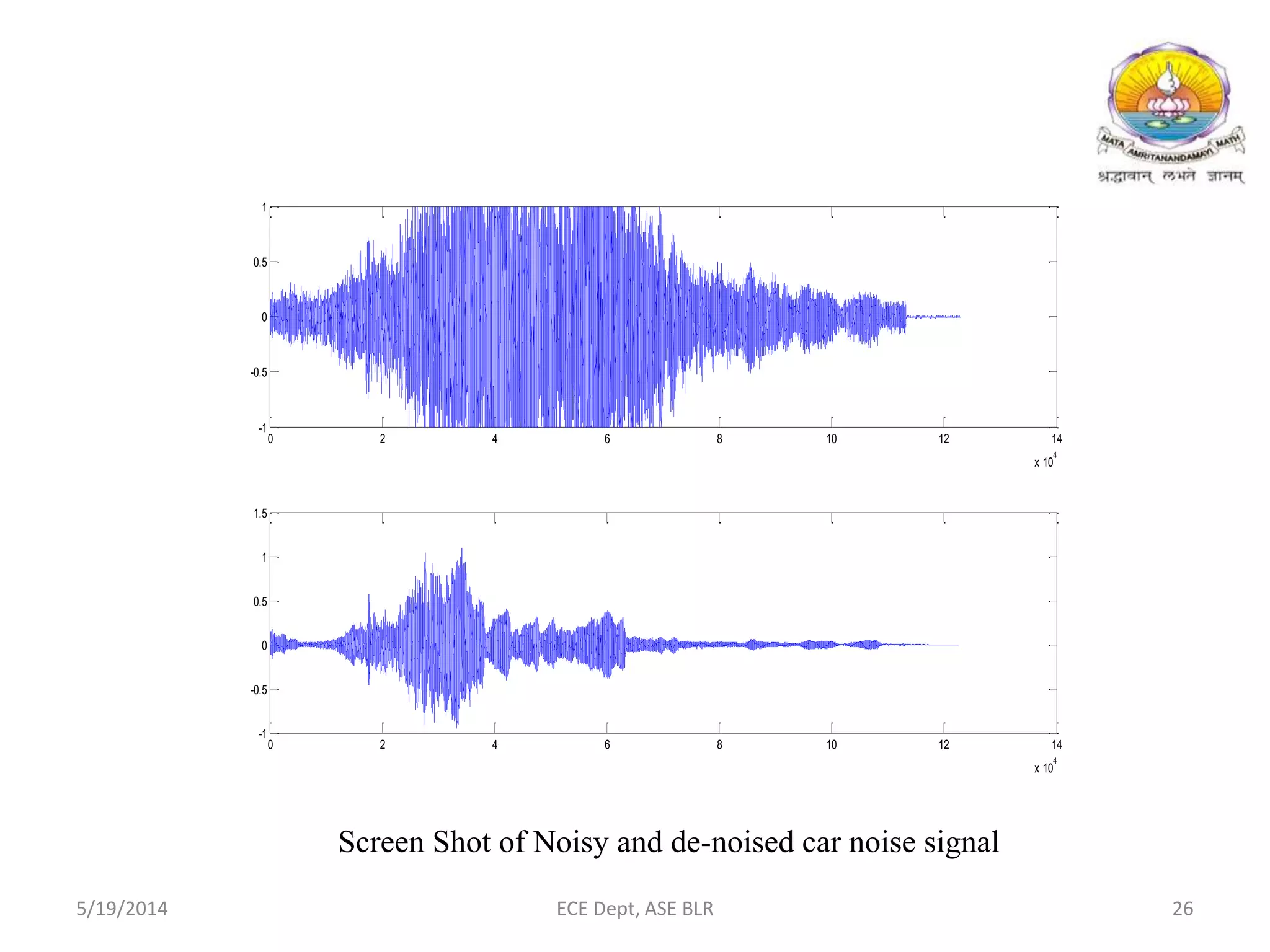
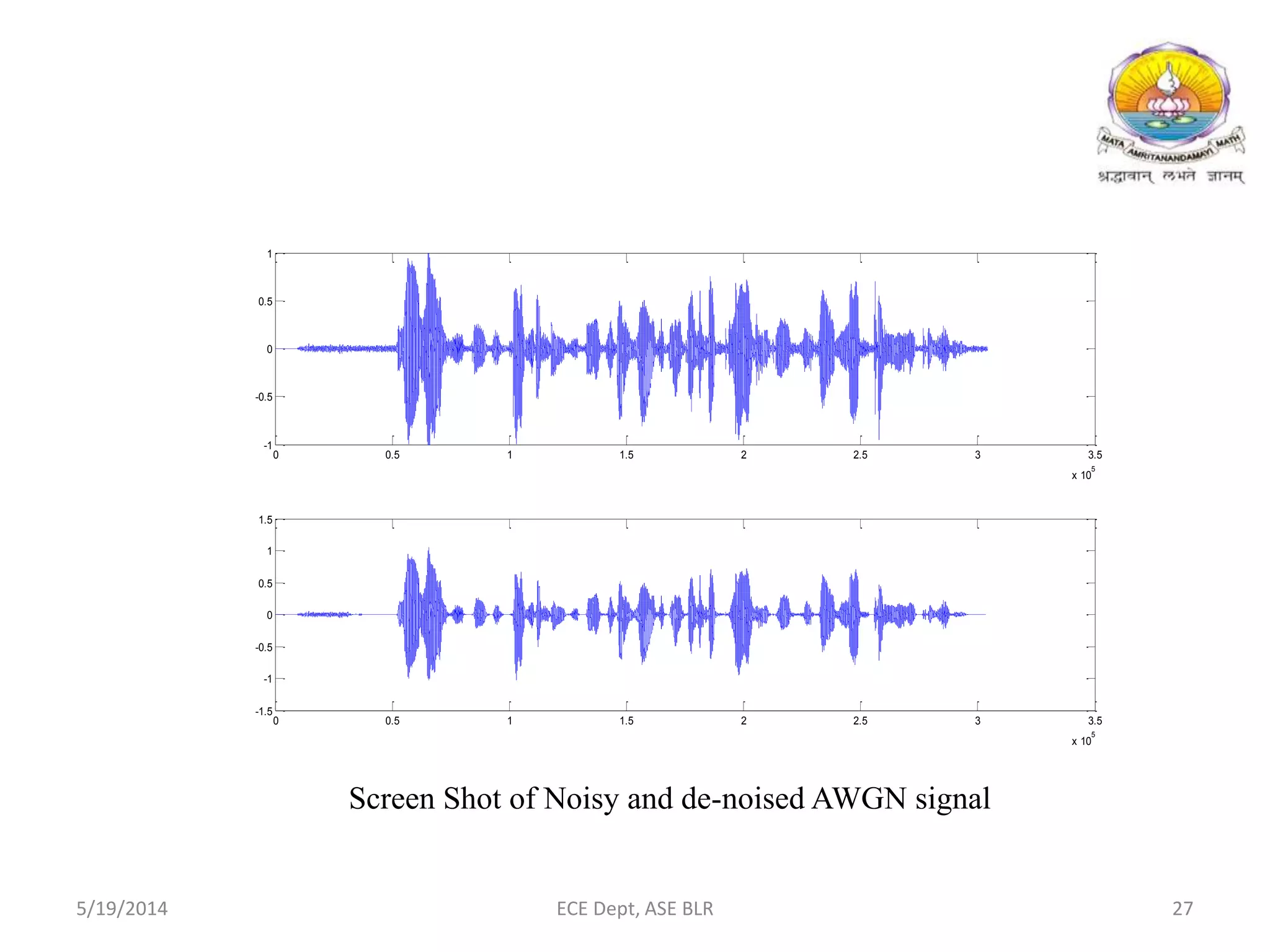
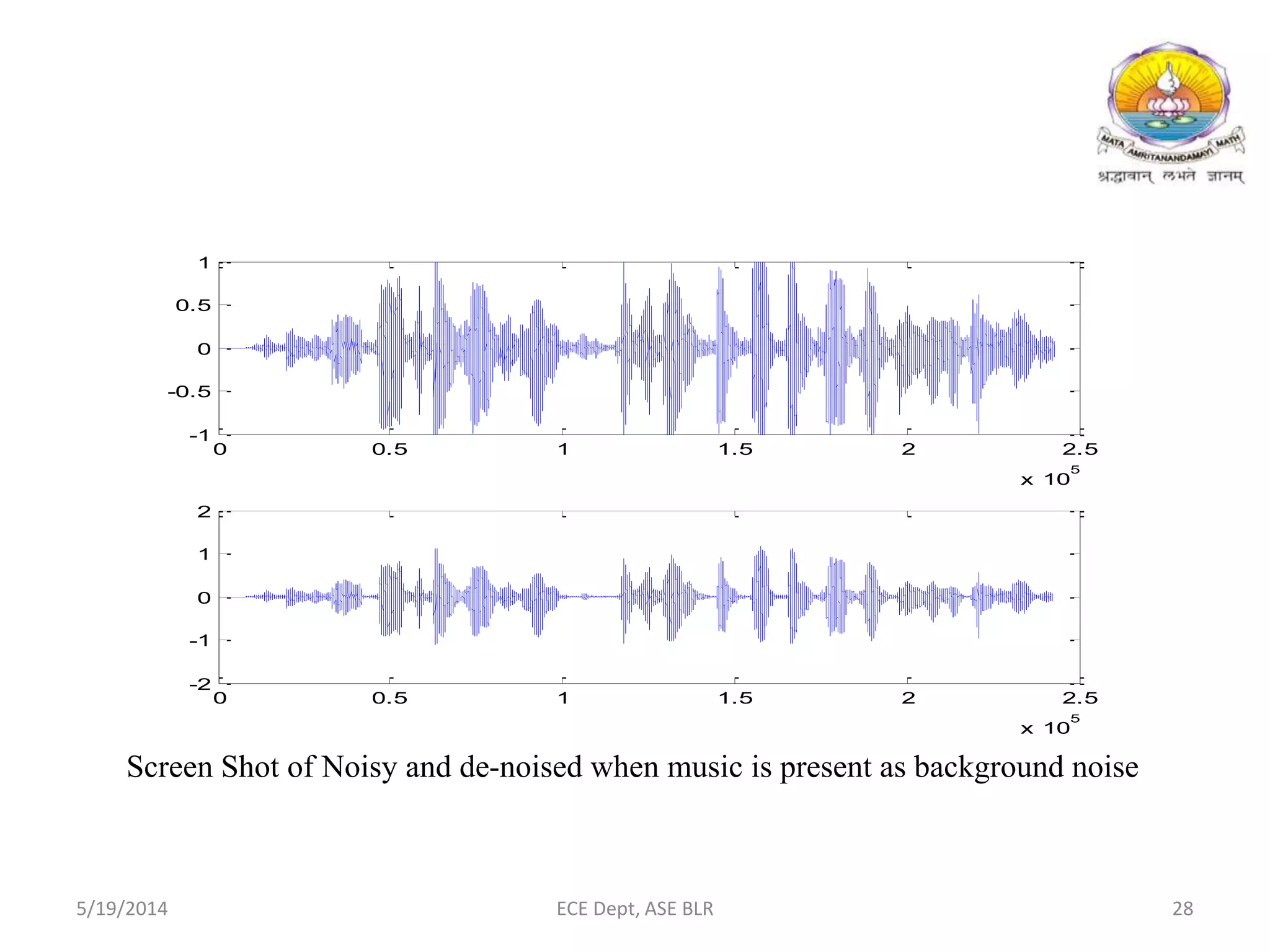
The document presents two methods for removing noise from speech signals: 1) using wavelet theory, where noisy signals are decomposed into high and low frequency components and thresholds are applied to remove noise, and 2) a geometric approach to spectral subtraction that models noisy speech in the complex plane and estimates noise without assuming cross terms are zero. Simulation results show both methods can successfully reduce noise like babble, white noise, music, and AWGN from speech signals.

1. A GEOMETRIC APPROACH TO SPECTRAL
SUBSTRACTION AND ADDITIVE WHITE GAUSSIAN
NOISE REMOVAL USING WAVELETS
P. S. Manasa :BL.EN.U4ECE10138
Keerthi Thallam :BL.EN.U4ECE10190
Guided by
Dr. Shikha Tripathi
Presented by
5/19/2014 ECE Dept, ASE BLR 1

2. Contents
• Introduction
• Outline of mid-semester presentation
• White noise
• Wavelet theory
• De-noising using wavelet theory
1. Algorithm
2. Simulation results
3. Conclusion
• A Geometric approach to Spectral Subtraction
1. Algorithm
2. Simulation results
3. Conclusion
5/19/2014 ECE Dept, ASE BLR 2

3. Introduction
• Speech enhancement (i.e removal noise from speech) is
necessary to improve user perception
• Noise degrades the quality of the information signal
• De-Noising plays a major role in communication
• Different de-noising techniques can be employed for different
noises
5/19/2014 ECE Dept, ASE BLR 3

4. Transient noise reduction using diffusion
filters
Estimation power spectral density (PSD) of the transient noise
by employing a NL neighborhood filter
• Modeling speech signal as an autoregressive (AR) process in
short-time frames
• Decorrelating the noisy measurement y(n) in each time frame
using the AR parameters
• Find Fourier transform coefficients in each frame and find the
PSD
5/19/2014 ECE Dept, ASE BLR 4

5. Transient noise reduction using diffusion
filters (Contd…)
• Modeling transient noise d(n) as d(n) = h(n) ∗ (b(n)v(n))
• Kernel to find out frames with and without transient noise
5/19/2014 ECE Dept, ASE BLR 5

6. Methods Implemented
Method 1: Reduction of noise(AWGN) using
wavelets (Roopali Goel et al.,2013)
Method 2: Geometric approach to spectral
subtraction (Yang Lu et al.,2008)
5/19/2014 ECE Dept, ASE BLR 6

7. White Noise
• Impulse autocorrelation function
• Flat power spectrum(equal power in all
frequencies)
a) Time-domain signal b) Autocorrelation c) PSD
5/19/2014 ECE Dept, ASE BLR 7

8. Wavelets
• Low frequency components gives the speech
its identity
5/19/2014 ECE Dept, ASE BLR 8

9. Multiple Level Decomposition
• The decomposition process can be iterated,
with successive approximations
5/19/2014 ECE Dept, ASE BLR 9

10. De-Noising Using Wavelets
Algorithm
• Noisy signal should be decomposed into tree of high and low
frequency components.
• For any particular level of the decomposed signal (tree)
wavelet coefficients should be found out.
• Tree level should be selected such that it gives better
performance.
• Threshold should be fount out using ‘Birge-Massart’
algorithm
• Using the threshold value soft thresholding of the high
frequency components is done .
5/19/2014 ECE Dept, ASE BLR 10
(Roopali Goel et al.,2013)

11. Simulation Results
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
x 10
4
-0.2
0
0.2
0.4
0.6
time
Amplitude
original signal
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
x 10
4
-0.2
-0.1
0
0.1
0.2
time
Amplitude
Noisy signal
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
x 10
4
-0.2
-0.1
0
0.1
0.2
time
Amplitude
Denoised signal
5/19/2014 ECE Dept, ASE BLR 11
De-Noising noisy speech signal

12. De-Noising sinusoidal signal
0 500 1000 1500 2000 2500
-1
0
1
time
Amplitude
original signal
0 500 1000 1500 2000 2500
-2
0
2
time
Amplitude
Noisy signal
0 500 1000 1500 2000 2500
-2
0
2
time
Amplitude
Denoised signal
5/19/2014 ECE Dept, ASE BLR 12

13. Correlation b/w original and de-noised
signal
-20 -15 -10 -5 0 5 10 15 20
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
coif 5
lag
samplecrosscorrelation
Correlation @ 0
5/19/2014 ECE Dept, ASE BLR 13

14. Conclusion
• Successfully able to remove AWGN
• A high correlation value above 98% at lag
value of zero has been achieved
5/19/2014 ECE Dept, ASE BLR 14

15. A geometric approach to spectral
subtraction (Yang Lu et al.,2008)
• Does not suffer from musical noise distortion
• Does not assume that the cross terms are zero
• Performs significantly better than the traditional spectral subtractive
algorithm
• Based on representing the noisy speech spectrum in the complex plane
as the sum of the clean signal and noise vectors
5/19/2014 ECE Dept, ASE BLR 15

16. • let y(n) = x(n) + d(n)
Where y(n)= sampled noisy speech signal
x(n)= clean signal
d(n)= noise signal
•Taking the short-time Fourier transform of y(n)
Where N is the frame length in samples
• Short-term power spectrum of the noisy speech
Algorithm
5/19/2014 ECE Dept, ASE BLR 16

17. • Relative error introduced when neglecting the cross terms is
given by
• Relative error in terms of true SNR in frequency bin k
Algorithm(Contd…)
5/19/2014 ECE Dept, ASE BLR 17

18. • Equation of noisy speech signal in polar form
Representation of Noise spectrum in complex plane as the sum of clean
signal spectrum and noise spectrum
Algorithm(Contd…)
5/19/2014 ECE Dept, ASE BLR 18

19. •New gain function with out assuming cross terms to be equal
to zero is
• Using cosine rule
Algorithm(Contd…)
5/19/2014 ECE Dept, ASE BLR 19

20. •Dividing both numerator and denominator of cxd and cyd by
aD^2 we get
Where
a posteriori SNR
a priori SNR
So
Algorithm(Contd…)
5/19/2014 ECE Dept, ASE BLR 20

21. • Instantaneous estimate of γ is
• To avoid rapid fluctuations smoothing of γ is done as follows
Algorithm(Contd…)
5/19/2014 ECE Dept, ASE BLR 21

22. • Does not use a voice activity detector
• Tracks spectral minima in each frequency band
• Optimally smoothed power spectral density is estimated
• Develops an unbiased noise power spectral density estimator
Noise Power Spectral Density
Estimation
5/19/2014 ECE Dept, ASE BLR 22

23. Smoothing of PSD
where smoothing parameter is
5/19/2014 ECE Dept, ASE BLR 23

24. Unbiased estimator of the noise power
spectral density
5/19/2014 ECE Dept, ASE BLR 24

25. Simulation Result
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
x 10
4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
x 10
4
-0.4
-0.2
0
0.2
0.4
Screen Shot of Noisy and de-noised speech signal(babble)
5/19/2014 ECE Dept, ASE BLR 25

26. 0 2 4 6 8 10 12 14
x 10
4
-1
-0.5
0
0.5
1
1.5
0 2 4 6 8 10 12 14
x 10
4
-1
-0.5
0
0.5
1
Screen Shot of Noisy and de-noised car noise signal
5/19/2014 ECE Dept, ASE BLR 26

27. Screen Shot of Noisy and de-noised AWGN signal
0 0.5 1 1.5 2 2.5 3 3.5
x 10
5
-1.5
-1
-0.5
0
0.5
1
1.5
0 0.5 1 1.5 2 2.5 3 3.5
x 10
5
-1
-0.5
0
0.5
1
5/19/2014 ECE Dept, ASE BLR 27

28. 5/19/2014 ECE Dept, ASE BLR 28
0 0.5 1 1.5 2 2.5
x 10
5
-2
-1
0
1
2
0 0.5 1 1.5 2 2.5
x 10
5
-1
-0.5
0
0.5
1
Screen Shot of Noisy and de-noised when music is present as background noise

29. Conclusion
• Successfully able to reduce several types of
noise like babble, white , music , AWGN
• It shows better performance compared to that
of traditional spectral subtraction algorithms
• It can remove noise from low as well as high
SNR speech
5/19/2014 ECE Dept, ASE BLR 29

30. Future Scope
• De-noising the signal without assuming that
the first 5 frames is only noise.
• To remove the background noise completely
5/19/2014 ECE Dept, ASE BLR 30

31. References
• Roopali Goel, Ritesh Jain “Speech Signal Noise Reduction by Wavelets”
International Journal of Innovative Technology and Exploring Engineering
(IJITEE) ISSN: 2278-3075, Volume-2, Issue-4, March 2013
• Yang Lu, Philipos C. Loizou “A geometric approach to spectral subtraction”
Department of Electrical Engineering, University of Texas-Dallas, Richardson,
TX 75083-0688, United States 24 January 2008.
• Adrian E. Villanueva- Luna1, Alberto Jaramillo-Nuñez1, Daniel Sanchez-
Lucero1, Carlos M. Ortiz-Lima1,J. Gabriel Aguilar-Soto1, Aaron Flores-Gil2 and
Manuel May-Alarcon “Denoising audio signals” using matlab Instituto
Nacional de Astrofisica, Optica y Electronica (INAOE) Universidad Autonoma
del Carmen (UNACAR) Mexico.
• Martin R., 2001. Noise power spectral density estimation based on
optimal smoothing and minimum statistics. IEEE Trans. Speech
Audio Process. 9 (5), 504–512
5/19/2014 ECE Dept, ASE BLR 31