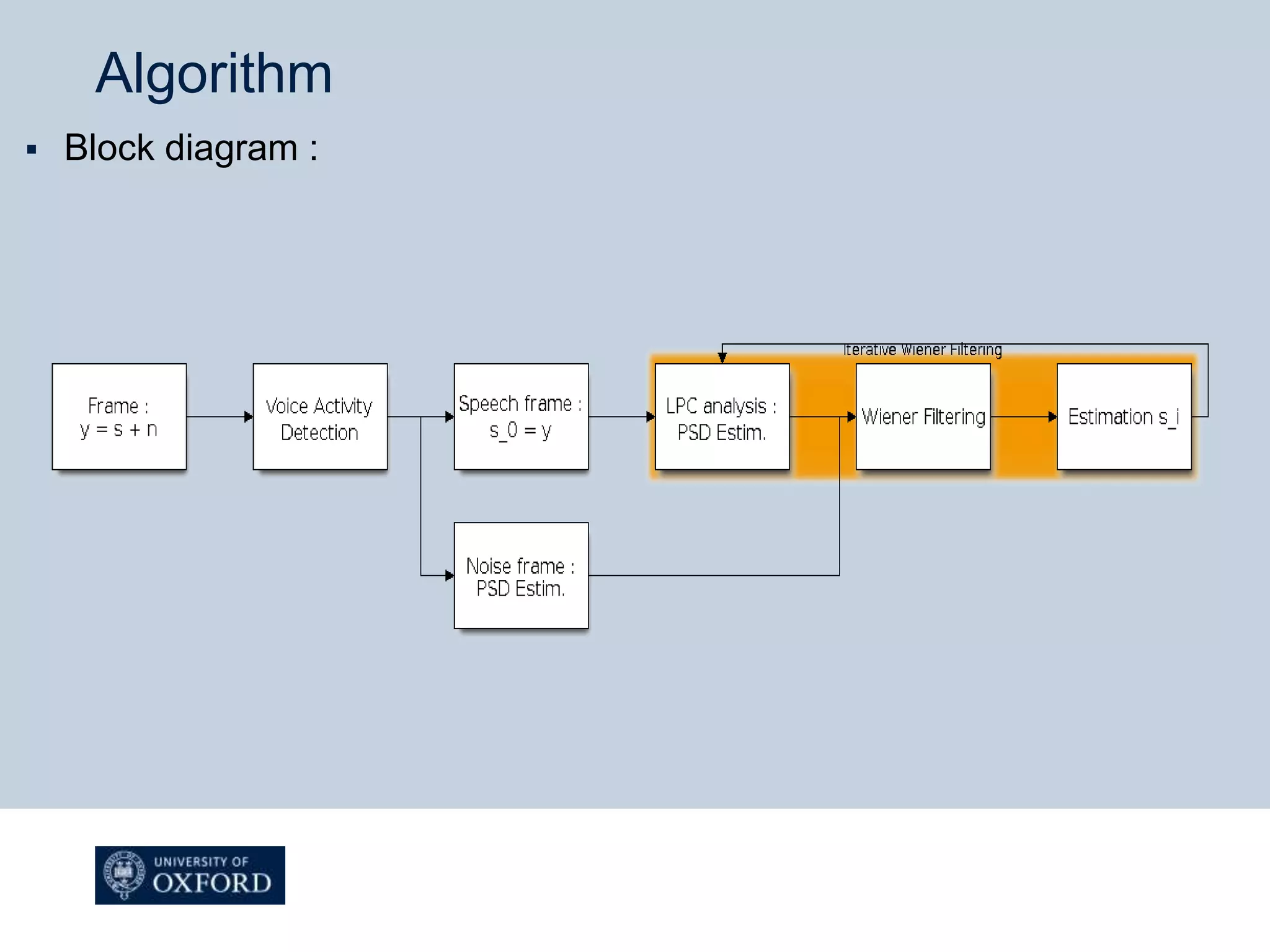
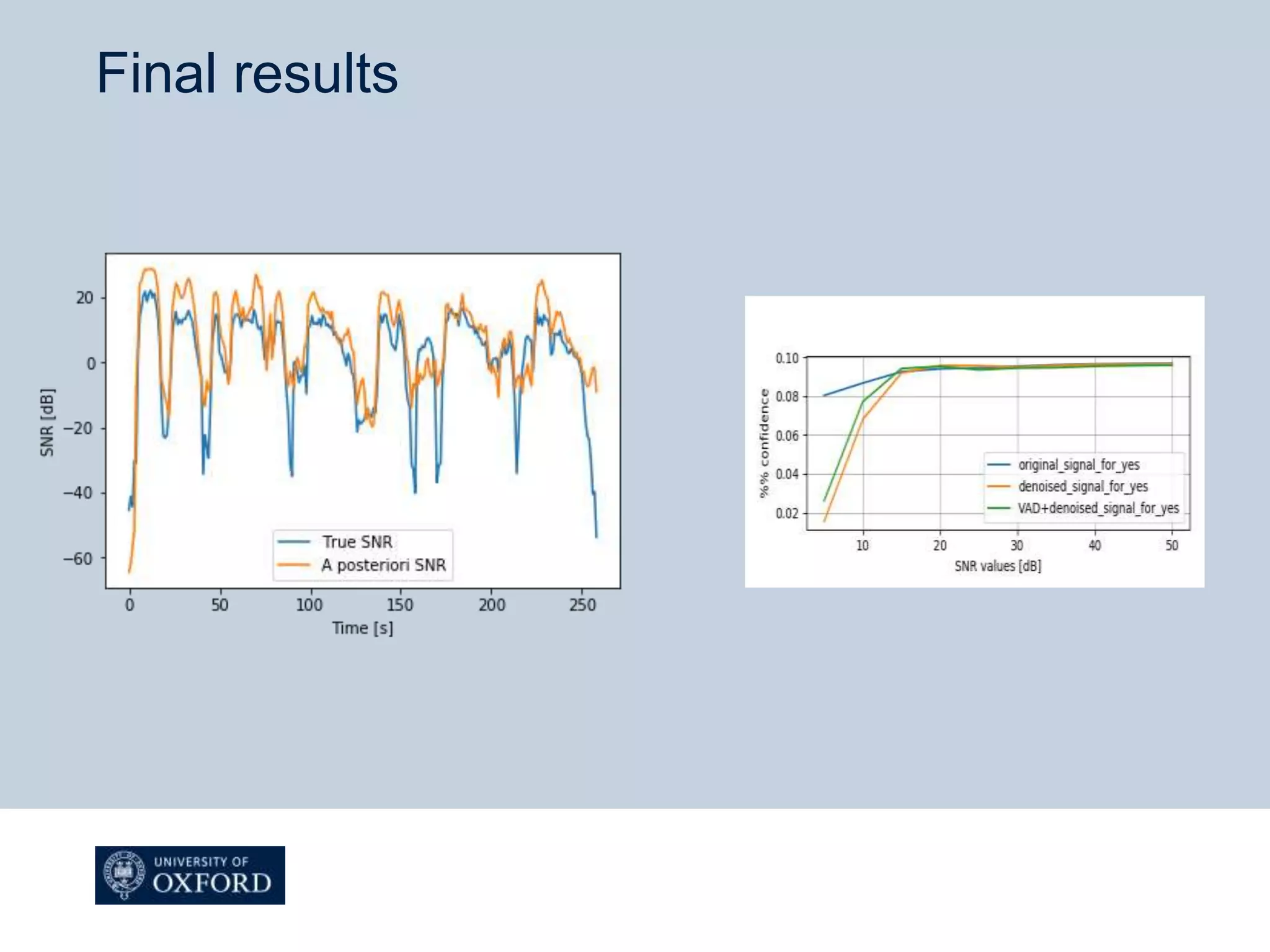
The document describes a Wiener filtering algorithm for noise suppression in speech signals. It involves estimating the noise and speech power spectral densities (PSDs) using a noise model and all-pole modeling of speech respectively. An iterative Wiener filter is then constructed using the PSD estimates. The algorithm is improved by adding a voice activity detector to estimate noise PSD only from non-speech frames. Evaluation shows the denoised speech has higher intelligibility and a posteriori SNR compared to noisy speech.

1. Noise Suppression using Wiener Filtering
Swayam Mittal, Richard Gormley
Acoustic Signal Processing
OXDS 2017-2018

2. Topics
 Algorithm
 Wiener Filtering
 Noise Power Spectral Distribution (PSD) estimation
 Speech PSD estimation : all-pole model
 Voice Activity Detector
 Results
 Evaluation metrics
 Sentence and word denoising
 Conclusion

3. Algorithm
 Block diagram :

4. Algorithm (2)
 Iterative Wiener Filter construction
𝐻 𝜔 =
𝑃𝑠(𝜔)
𝑃𝑠 𝜔 + 𝑃𝑛(𝜔)
Where 𝑃𝑠 and 𝑃𝑛 are the power spectral density (PSD) of respectively
the speech and the noise
 Noise PSD estimation :
 Assume noise follows a Gaussian distribution
𝑃𝑛 𝜔 = 𝜎 𝑛
2
 Estimation of the standard deviation based on the previous frames
𝜎 𝑘 = 1 − 𝛼 ⋅ 𝜎 𝑘−1 + 𝛼 ⋅ 𝜎𝑙𝑜𝑐

5. Algorithm (3)
 Speech PSD estimation : all-pole modeling
 Auto-regressive process
𝑠 𝑙 =
𝑘=1
𝑝
𝑎 𝑘 𝑠 𝑙 − 𝑘 + 𝑔 ⋅ 𝑤 𝑙
 Where 𝑔 is a gain factor, 𝑤 𝑙 is a simple periodic excitation, 𝑎 𝑘 is the DFT
coefficient
 The estimated PSD is given by :
𝑃𝑠 𝜔 =
𝑔2
1 − 𝑘=1
𝑝
𝑎 𝑘 𝑒−𝑗𝑘𝜔 2

6. Improving the algorithm ?
 Add Voice Activity Detector
 Allows to calculate 𝑃𝑛 𝜔 only on speechless frames
 Wiener filter computation is expensive
 Compute the signal energy level :
 𝐿 𝑛
=
1
𝐾 𝑘=0
𝐾−1
𝑊𝑘 ⋅ 𝑌𝑘
𝑛
2
 Where 𝑊𝑘 is a weighting function and 𝑌𝑘
𝑛
is the DFT of frame
𝑛

7. Improving the algorithm (2)
 Dual constant estimator :
 Estimate the floor noise level 𝐿 𝑚𝑖𝑛
(𝑛)
using an iterative process :
𝐿 𝑚𝑖𝑛
(𝑛)
=
1 −
𝑇
𝜏 𝑢𝑝
𝐿 𝑚𝑖𝑛
𝑛−1
+
𝑇
𝜏 𝑢𝑝
𝐿 𝑚𝑖𝑛
𝑛−1
, 𝐿 𝑛
> 𝐿 𝑚𝑖𝑛
(𝑛−1)
1 −
𝑇
𝜏 𝑑𝑜𝑤𝑛
𝐿 𝑚𝑖𝑛
𝑛−1
+
𝑇
𝜏 𝑑𝑜𝑤𝑛
𝐿 𝑚𝑖𝑛
𝑛−1
, 𝐿 𝑛 ≤ 𝐿 𝑚𝑖𝑛
(𝑛−1)
where 𝑇 is the frame duration, 𝜏 𝑢𝑝 and 𝜏 𝑑𝑜𝑤𝑛 are the time constant to
track the noise.

8. Improving the algorithm (3)
 Final decision :
 𝑉 𝑛
=
0, if
𝐿 𝑛
𝐿 𝑚𝑖𝑛
(𝑛) > 𝑇𝑑𝑜𝑤𝑛
1, if
𝐿 𝑛
𝐿 𝑚𝑖𝑛
(𝑛) > 𝑇𝑑𝑜𝑤𝑛
𝑉 𝑛−1
, otherwise

9. Evaluation
 A posteriori SNR
 Build estimate of noise
 Compute SNR of the denoised signal
 Intelligibility
 A network is asked to classify speech signals at various SNR ratios,
and we compare its classification certainty for noisy speech and
denoised speech

10. Final results

11. Conclusion
 We have shown an algorithm used for speech denoising
 Based on LPC modelling
 The necessity of a VAD has been established
 For low SNR, a statistical model could be developped
 Lower computation time
 We improved the a posteriori SNR for all the noisy speech
samples
 Can be improved by correctly tuning the parameters in the
code

12. Questions ?