Download to read offline
Uploaded byFrank Ong
Fast Sparse 2-D DFT Computation using Sparse-Graph Alias Codes
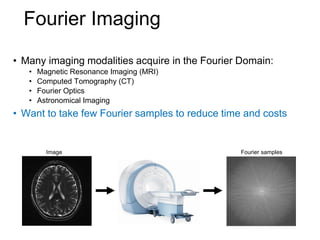
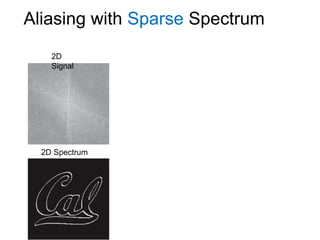
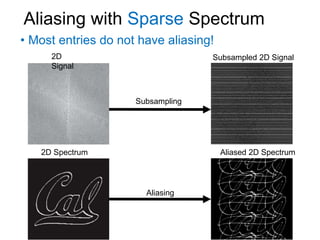
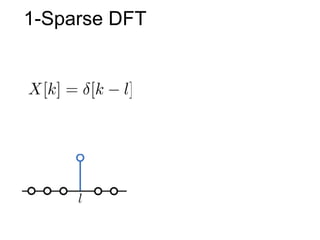
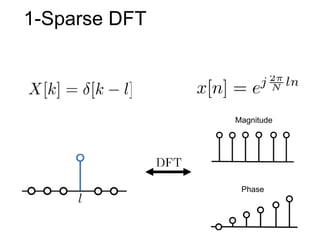
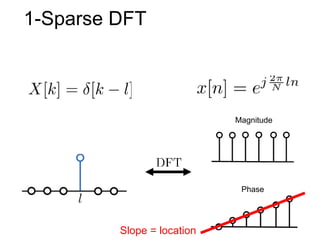
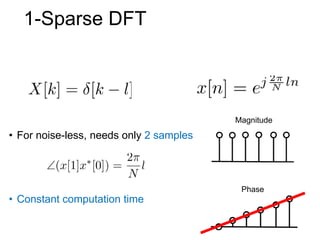
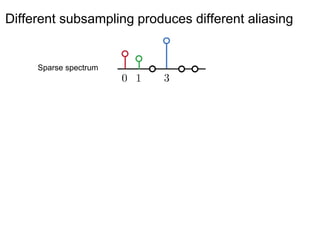
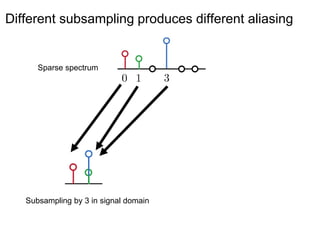
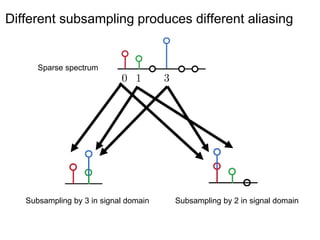
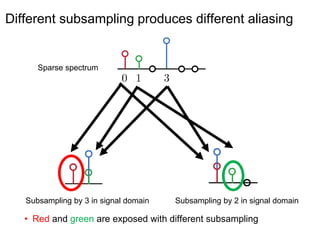
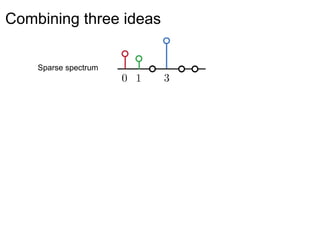
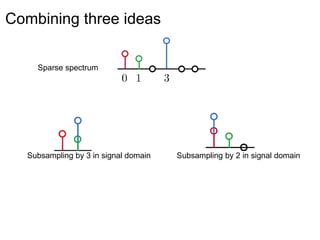
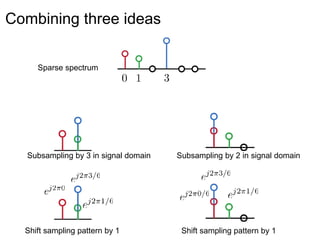
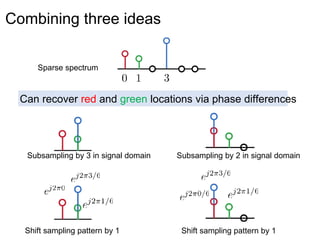
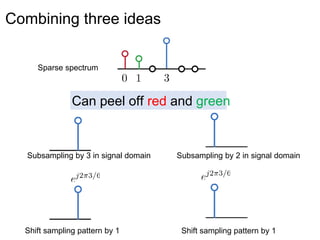
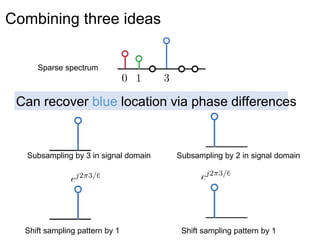
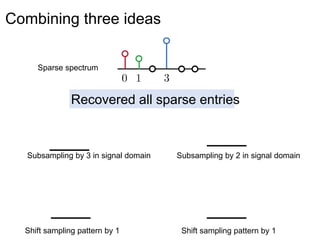
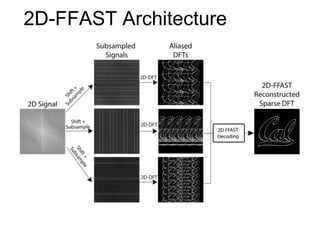
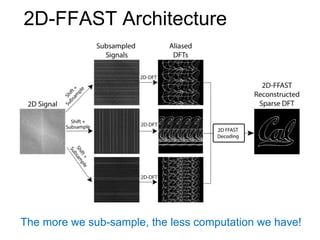
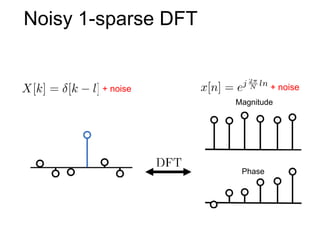
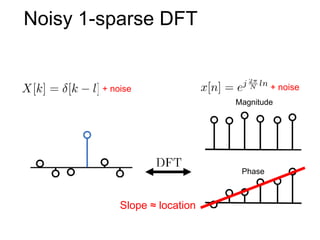
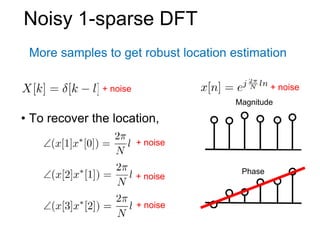
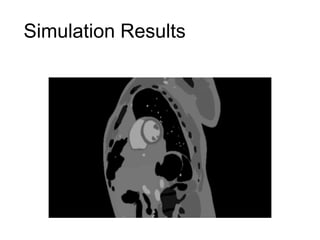
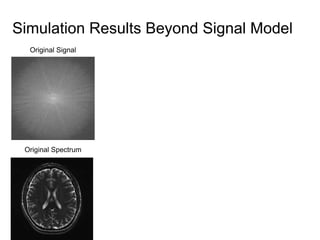
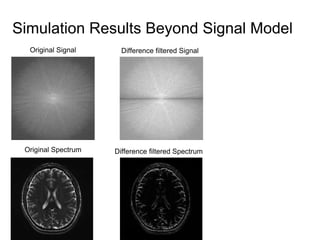
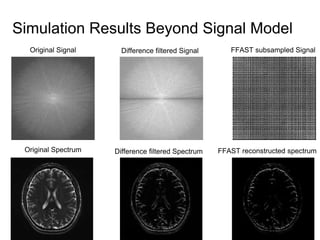
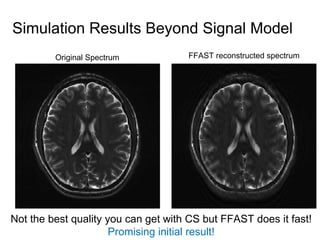
This document presents a method called 2D-FFAST (Fast Fourier-Aliasing-based Sparse Transform) that enables fast computation of sparse 2D discrete Fourier transforms (DFTs). It generalizes a previous 1D method to exploit sparsity and allow sub-Nyquist sampling rates. The key ideas are: 1) aliasing patterns from different subsampling reveal sparse entries, 2) choosing co-prime subsampling factors provides diverse patterns, and 3) combining patterns recovers the sparse spectrum. Simulations demonstrate reconstruction of medical images from highly subsampled measurements in both ideal sparse models and more realistic settings.
More Related Content
Similar to Fast Sparse 2-D DFT Computation using Sparse-Graph Alias Codes
Fast Sparse 2-D DFT Computation using Sparse-Graph Alias Codes
- 1. Fast Sparse 2-DDFT Computation using Sparse-Graph Alias Codes Frank Ong, Sameer Pawar and Kannan Ramchandran
- 2. • Many imagingmodalities acquire in the Fourier Domain: • Magnetic Resonance Imaging (MRI) • Computed Tomography (CT) • Fourier Optics • Astronomical Imaging • Want to take few Fourier samples to reduce time and costs Image Fourier samples Fourier Imaging
- 3. • Exploits sparsityto go beyond Nyquist rate • Provides good reconstructed images • Most algorithms alternate between Fourier and image domain • >100 FFTs! >10-minute reconstruction! Loading… Compressed Sensing
- 4. • Goal: Fastin both acquisition and reconstruction • Real-time reconstruction • Many previous works in sparse FFT: • Gilbert et al. 2002 • Indyk et al. 2012 • Hassanieh et al. 2014 • Iwen 2010 • And many more… • Mostly 1D results • This work: • Generalizes 1D-FFAST framework of Pawar & Ramchandran 2013 • Illustrate 3 key ideas This Work: 2D-FFAST (Fast-Fourier-Aliasing-based-Sparse-Transform)
- 5. 2D Spectrum Aliasing withDense Spectrum 2D Signal
- 6. Aliasing 2D Spectrum Aliased2D Spectrum Aliasing with Dense Spectrum • Everything gets aliased on top of each other 2D Signal Subsampled 2D Signal Subsampling
- 7. 2D Spectrum Aliasing withSparse Spectrum 2D Signal
- 8. Aliasing 2D Spectrum Aliased2D Spectrum Aliasing with Sparse Spectrum • Most entries do not have aliasing! 2D Signal Subsampling Subsampled 2D Signal
- 9.
- 10.
- 11.
- 12. • For noise-less,needs only 2 samples • Constant computation time 1-Sparse DFT Magnitude Phase
- 13. Different subsampling producesdifferent aliasing Sparse spectrum
- 14. Different subsampling producesdifferent aliasing Sparse spectrum Subsampling by 3 in signal domain
- 15. Different subsampling producesdifferent aliasing Sparse spectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain
- 16. Different subsampling producesdifferent aliasing Sparse spectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain • Red and green are exposed with different subsampling
- 17. Combining three ideas Sparsespectrum
- 18. Combining three ideas Sparsespectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain
- 19. Combining three ideas Sparsespectrum Shift sampling pattern by 1 Subsampling by 3 in signal domain Subsampling by 2 in signal domain Shift sampling pattern by 1
- 20. Combining three ideas Sparsespectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain Can recover red and green locations via phase differences Shift sampling pattern by 1 Shift sampling pattern by 1
- 21. Combining three ideas Sparsespectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain Shift sampling pattern by 1 Shift sampling pattern by 1 Can peel off red and green
- 22. Combining three ideas Sparsespectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain Can recover blue location via phase differences Shift sampling pattern by 1 Shift sampling pattern by 1
- 23. Combining three ideas Sparsespectrum Subsampling by 3 in signal domain Subsampling by 2 in signal domain Recovered all sparse entries Shift sampling pattern by 1 Shift sampling pattern by 1
- 24.
- 25. 2D-FFAST Architecture The morewe sub-sample, the less computation we have!
- 26. • How topick sampling factors to get diverse aliasing patterns? • Clearly subsampling by 2 and 4 do not work • 1D (Pawar and Ramchandran 2013): • Based on the Chinese Remainder Theorem • Sampling factors should be relatively co-prime • For example, subsample by 40, 41, and 43 • 2D (This work): • Product of 2D subsampling factors should be relatively co-prime • For example, subsample by (5, 5), (6, 6) and (7, 7) Sampling Factors 25 36 49
- 27. Theoretical Guarantee • Fora input that satisfies the dimension assumption • The 2D-FFAST computes its k-sparse 2D-DFT w.h.p: • ~4k measurements for almost all sublinear sparsity • O(k log k) computation complexity • For more details: http://arxiv.org/abs/1509.05849v1.
- 28. + noise +noise Magnitude Phase Noisy 1-sparse DFT
- 29. + noise +noise Magnitude Phase Noisy 1-sparse DFT Slope ≈ location
- 30. + noise + noise Magnitude Phase Noisy1-sparse DFT • To recover the location, + noise + noise + noise More samples to get robust location estimation
- 31. Theoretical Guarantee • Foran N = Nx x Ny input • The 2D-FFAST computes its k-sparse 2D-DFT w.h.p: • O(k log3 N) measurements • O(k log4 N) computation complexity • For more details: http://arxiv.org/abs/1509.05849v1.
- 32. Original Signal Sub-sampledSignal Reconstructed Spectrum Simulation Results Image size: 280 x 280 = 78,400 Sparsity: 3509 Measurements: 4.75 k = 16,668
- 33.
- 34.
- 35.
- 36. Simulation Results BeyondSignal Model Original Signal Original Spectrum
- 37. Original Signal Differencefiltered Signal Difference filtered SpectrumOriginal Spectrum Simulation Results Beyond Signal Model
- 38. Original Signal Differencefiltered Signal Difference filtered SpectrumOriginal Spectrum FFAST subsampled Signal FFAST reconstructed spectrum Simulation Results Beyond Signal Model
- 39. Original Spectrum FFASTreconstructed spectrum Not the best quality you can get with CS but FFAST does it fast! Promising initial result! Simulation Results Beyond Signal Model
- 40. Conclusion • Fast inboth acquisition and reconstruction • Illustrate 2D-FFAST architecture through 3 key ideas • Coding theory guided reconstruction method • https://github.com/UCBASiCS/FFAST.git Thank you!
Editor's Notes
- #4 Real time mri illustraiton
- #5 Enable Real time recovery and robust to noise Remove without… dates cite
- #12 Put label
- #13 Put label
- #14 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #15 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #16 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #17 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully We need diversity
- #18 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #19 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #20 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #21 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #22 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #23 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #24 Non-sparse aliasing -> Sparse aliasing -> Pick sampling factors carefully
- #25 Add box to decoding
- #26 Add box to decoding
- #27 Example Theorem Cite sameer Invokes Chinese Remainder Theorem
- #28 With high prob 4k measurements Usefuly for sub-linear n
- #29 Put label
- #30 Put label
- #31 Put label
- #32 Example! Numbers Details!
- #33 Put N
- #35 Video first
- #38 Beyond theory was meant for
- #39 Emphasize bonus. histogram
- #40 Emphasize bonus. histogram