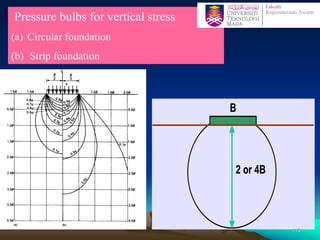
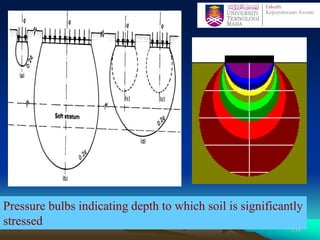
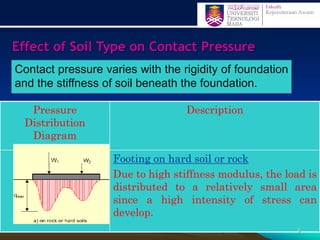
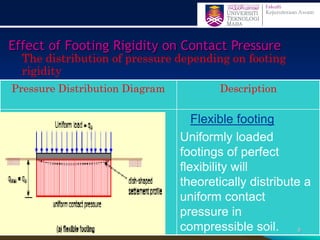
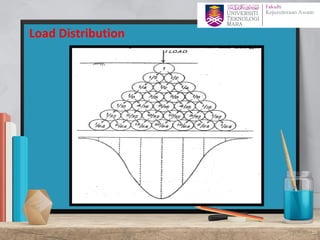
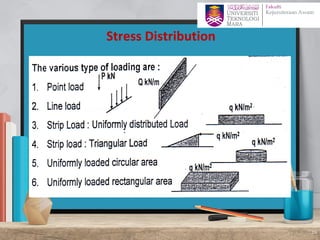
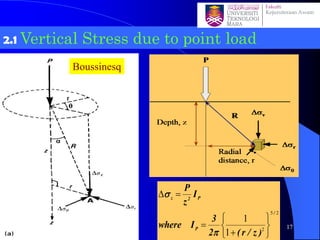
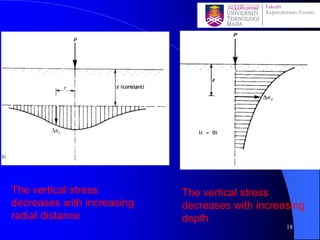
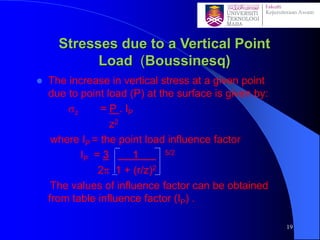
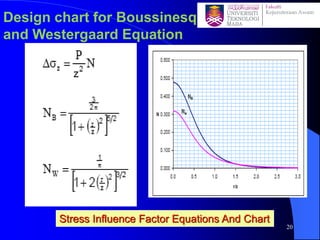
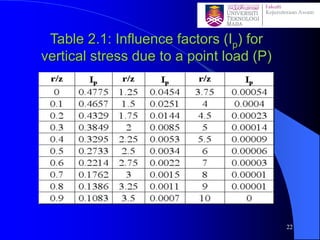
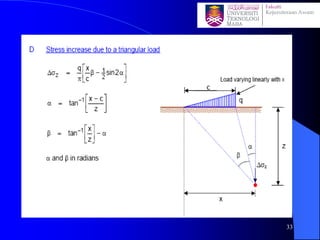
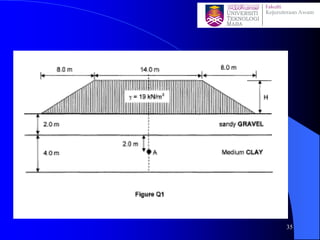
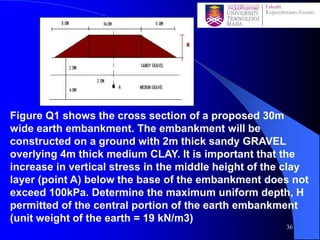
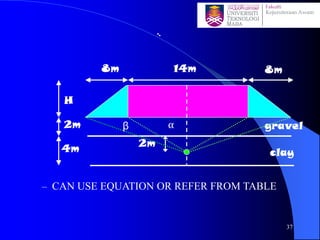
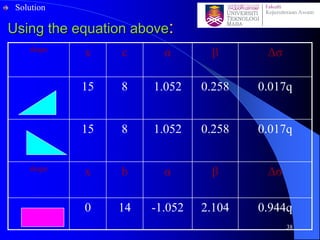
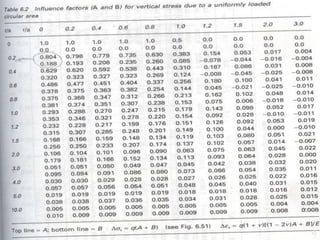
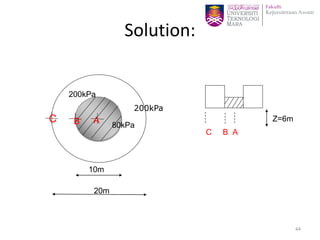
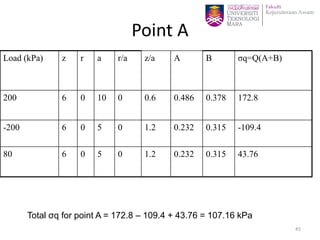
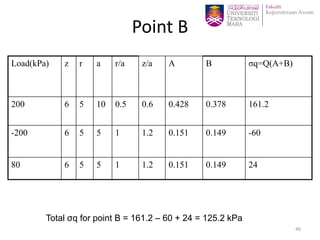
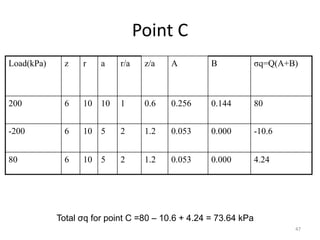
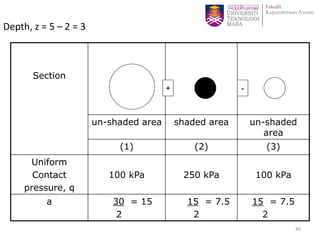
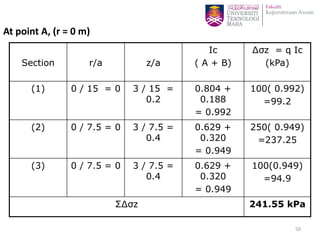
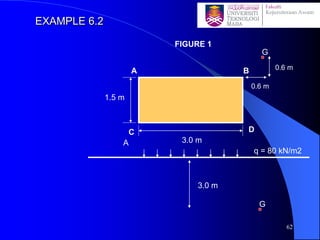
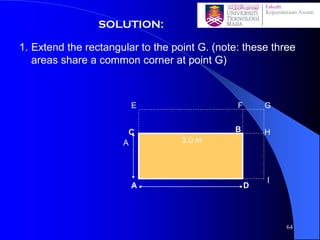
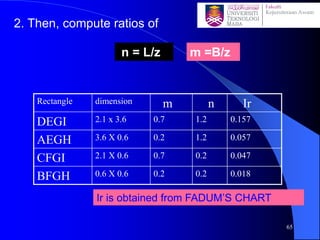
This document discusses stress distribution in soil due to various types of loading. It begins by introducing key concepts like how applied loads are transferred through the soil mass, creating stresses that decrease in magnitude but increase in area with depth. The factors that affect stress distribution, like loading size/shape, soil type, and footing rigidity are also covered. The document then examines specific load types - point loads, line loads, rectangular/triangular strip loads, and circular loads - providing the equations to calculate vertical stress increases below each. Several examples demonstrate calculating stress increases below compound load arrangements. The summary provides an overview of the key topics and calculations presented in the document.

1. CHAPTER 2:
STRESS DISTRIBUTION IN SOIL
At the end of this lecture, the students will be able to :
1. Identify and discuss all parameters required to
determine the increase in vertical stress below a
foundation subjected to different types of loading.
2. Formulate and evaluate the relevant increase in
vertical stress due to various types of loading and
footing shapes.
3. Formulate and evaluate vertical stress due to
rectangular loading and use Bulbs of Pressure
MAZIDAH MUKRI 1

2. Introduction
❖ Imposing load on the surface of the soil will
create stresses within the mass.
❖ The loading transferred to the soil mass will be
spread laterally with increasing depth from the
point or area of application.
❖ With increasing depth, the area over which
new stresses develop will increase but
magnitude will decrease.
2

3. Concept on Stress Increases in Soil
❑ The first step in many engineering calculation,
e.g. foundation design, retaining wall design,
slope stability, etc., is the determination of
total vertical stresses.
❑ The magnitude of total stresses in the soil will
change with changes in surface loading,
excavation and type of soil.
❑ In the design of walls, tunnels,culvert etc.,
horizontal stresses will also be required.
❑ The total stress at a point in a soil mass is
calculated from the unit weight of the soil and
the depth below ground surface.
3

4. Vertical and Horizontal Stresses
+ Any change in vertical total
stress (v) may also result in
a change in the horizontal
total stress (h) at the same
point.
z
v
h
4

5. Factors affecting stress distribution :
❑ Size and shape of footing
❑ Load distribution
❑ Contact pressure – depends on the rigidity
of footing and stiffness of foundation soil
❑ Modulus of Elasticity and Poisson’s ratio
❑ Position of rigid boundary
5

6. Effect of Soil Type on Contact Pressure
Contact pressure varies with the rigidity of foundation
and the stiffness of soil beneath the foundation.
Pressure
Distribution
Diagram
Description
Footing on hard soil or rock
Due to high stiffness modulus, the load is
distributed to a relatively small area
since a high intensity of stress can
develop.
6

7. Effect of Soil Type on Contact Pressure
Pressure
Distribution
Diagram
Description
Footing on stiff soil
Load is distributed laterally which produces
lower values of contact pressure
Footing on soft soil
The contact pressure on soil beneath
the foundation is distributed almost
uniformly.
7

8. Effect of Footing Rigidity on Contact Pressure
The distribution of pressure depending on footing
rigidity
Pressure Distribution Diagram Description
Flexible footing
Uniformly loaded
footings of perfect
flexibility will
theoretically distribute a
uniform contact
pressure in
compressible soil. 8

9. Effect of Footing Rigidity on Contact Pressure
Pressure Distribution
Diagram Description
Rigid footing on cohesive soil
A higher contact pressures will be
transmitted while settling uniformly.
However, extremely high edge stresses
cannot occur since the soil passes some of
its load inwards and produces the arc-like
distribution.
Rigid footing on cohesionless soil
Less contact pressure at the edges of
footing but higher at mid-footing due to higher
confining pressure. Uniform settlement will
occur in this case.
9

10. Load Distribution
10

11. ▪ When the loading on the surface of a soil mass
varies the normal and shear stresses within
change.
▪ Two methods namely the Boussinesq (1883)
and the Westergaard(1938) can be used to
estimated vertical stress below a foundation.
▪ The Boussinesq theory assumed the soil as a
homogeneous,elastic and isotropic medium.
▪ Westergaard assumed the soil to be an elastic
and solid medium.
Stresses due to Foundation Loading
11

12. ❑ Boussinesq Stress Distribution
❑ 19 th. – century French mathematician
❑ assumed soil as homogeneous, isotropic
(same properties in all directions) and
elastic.
❑ Publish solutions (1885) for stresses
beneath a point load applied at the surface.
Boussinesq Stress Distribution
12

13. Following the footsteps of Boussinesq, other
solutions were developed for both stresses
and displacements relating to different types
of loading, layers of thickness, multi-layered
masses and internally loaded masses :
+ Ahlvin and Ulery, 1962
+ Giroud, 1970
+ Newmark, 1942
+ Poulos and Davis, 1974
13

14. ❑ More suitable for thin layers of stratified
deposits
❑ Assumed that thin layers of homogeneous and
anisotropic material sandwiched between
closely spaced, infinitely thin sheets of rigid
material
❑ Permit compression but no lateral deformation
❑ Formula different from Boussinesq
Westergaard Stress Distribution
14

15. Types of Loading
❑ Point load
➢ based on Boussinesq
➢ based on Westergaard
❑ Line load
❑ Triangular load
❑ Strip load
❑ Uniformly loaded rectangular area
❑ Uniformly loaded circular area
* Only vertical stresses will be highlighted as this is the
stress component that normally results in settlement.
15

16. Stress Distribution
16

17. 2.1 Vertical Stress due to point load
25
2
1
1
/
P
P2z
)z/r(2
3
Iwhere
I
z
P






+
=
=


Boussinesq
17

18. z
r
The vertical stress
decreases with increasing
radial distance
z
z
The vertical stress
decreases with increasing
depth
18

19. ⚫ The increase in vertical stress at a given point
due to point load (P) at the surface is given by:
z = P . IP
z2
where IP = the point load influence factor
IP = 3 1 5/2
2 1 + (r/z)2
The values of influence factor can be obtained
from table influence factor (IP) .
Stresses due to a Vertical Point
Load (Boussinesq)
19

20. Design chart for Boussinesq
and Westergaard Equation
Stress Influence Factor Equations And Chart
20

21. EXAMPLE 1.1
Four column loads of 980kN, 800kN, 550kN and 700kN
respectively are located at the corners of a square of 4m side
on the surface of a soil mass. A culvert passes diagonally
across the square, directly under the 980kN and 550kN load,
and a depth ( to its top) of 4m. Calculate the vertical stress
imposed on the culvert due to the 980kN load by using
i) formula for the influence factor is IP = 3 1 5/2
2 1 + (r/z)2
ii) influence factor (IP) table.
550kN800kN
700kN980kN
4m
4m
21

22. Table 2.1: Influence factors (Ip) for
vertical stress due to a point load (P)
22

23. B-a- Long Uniform Per Unit Length
2.2 Stresses Due to a Long Line Load
23

24. Table 2.2: Influence factors (IL) for vertical
stress due to a line load (P)
24

25. Example 2.1
Figure below shows two line loads and a point load
acting at the ground surface. Determine the
increase in vertical stress at point A, which is
located at a depth of 1.5 m.
q2 = 10 kN/m q1 = 15 kN/m
P = 30 kN
2 m
A
z = 1.5 m
3 m
2 m
25

26. Stresses due to a Long Line Load
Solution:
( ) ( ) ( )
( ) ( ) ( )
( )( )( )
( )
( )( )( )
( )
( )( )
( )( ) ( ) 
2
mkN0.902=
++=








++
+
+
+
+
=








+
+
+
+
+
=
++=
012.0065.0825.0
5.143
5.1
2
303
5.14
5.1102
5.12
5.1152
zr
z
2π
3P
zxπ
z2q
zxπ
z2q
ΔσΔσΔσΔσ
2
5
222
3
222
3
222
3
2
5
22
3
222
2
3
2
222
1
3
1
3z2z1zz

26

27. 2.3 Uniform Strip Load
bb
load, q kPa
x
z
a
b
q
x
z
•Strip loading results
from strip foundations to
walls, retaining walls, etc.
•The length of a strip
load is very large
compared with the
breadth.
•the longitudinal strain
can be assumed to be
zero.
27

28. Stress increase due to a uniform strip load
28

29. Stresses Due to a Strip Load
Three parallel strip foundation, each 1.8 m wide and 3.6 m
apart centre to centre are founded at 1.2 m depth transmit
contact pressures of 240 kPa, 180 kPa and 200 kPa
respectively. Using the table of influence factor, Is , calculate
the intensity of vertical stresses due to combined load
beneath the centre of each footing at a depth of 3.0 m from
the ground surface.
240kPa 180kPa 200kPa
3.6m 3.6m
3m
1.2m
A CB
Example 3.1

30. Solution:

31. ⚫ A triangular load occurs when the contact pressure
varies linearly across the breadth of the strip from zero
to a maximum value.e.g. below the sloping sides of an
embankment.
⚫ The vertical stress z is given by
z = qIT
where IT can be obtained from table influence factor (IT)
2.4 Stresses due to a Triangular Strip Load
31

32. Triangular Strip Load Distribution
Load varying linearly with x
c/2 c/2
q
z
r
a
b
32Vertical stress Oct 2020_MM

33. 33

34. 34
EXAMPLE 4.1

35. 35

36. Figure Q1 shows the cross section of a proposed 30m
wide earth embankment. The embankment will be
constructed on a ground with 2m thick sandy GRAVEL
overlying 4m thick medium CLAY. It is important that the
increase in vertical stress in the middle height of the clay
layer (point A) below the base of the embankment does not
exceed 100kPa. Determine the maximum uniform depth, H
permitted of the central portion of the earth embankment
(unit weight of the earth = 19 kN/m3)
36

37. – CAN USE EQUATION OR REFER FROM TABLE
14m8m 8m
H
2m
4m
gravel
clay
2m
αβ
37

38. shape
x c α β Δσ
15 8 1.052 0.258 0.017q
15 8 1.052 0.258 0.017q
shape
x b α β Δσ
0 14 -1.052 2.104 0.944q
Solution
Using the equation above:
38

39. q=γH
⚫ 0.034q+0.944q=100
0.978q=100
q=102.249 kPa
H= q = 102.249= 5.382m
γ 19
39

40. 2.5 Stresses Due to a Uniformly
Loaded Circular Area
+ For a uniformly loaded circular areas, e.g. raft
foundations, tank bases, etc., the basic
Boussinesq expressions are integrated over
the area.
+ An exact solution can be found for the increase
in vertical stress under the centre, but for
points offset from the centre an approximate
method has to be used.
40

41. Stresses Due to a Uniformly Loaded
Circular Area
r
r
z
R

z

r

q
aa
a) Stress beneath centre of circle
b) General vertical stress case
z = qIc =q (A+B)
Parameters = r/a & z/a
Where;
a = radius (m)
z = depth (m)
r = distance from the center to
the point (m)
41

42. 42

43. Figure shows the plan of a large circular raft foundation; the centre
(shaded) area transmits a contact pressure of 80 kPa and outer
annular area transmits a contact pressure of 200 kPa. Using the
factors in Table 6.2, calculate the intensity of vertical stress induced
at points in the soil mass below A, B and C. (z=6m)
C B A
10m
20m
43
EXAMPLE 5.1

44. Solution:
200kPa
C B A
10m
20m
80kPa
Z=6m
AC B
200kPa
44

45. Point A
Load (kPa) z r a r/a z/a A B σq=Q(A+B)
200 6 0 10 0 0.6 0.486 0.378 172.8
-200 6 0 5 0 1.2 0.232 0.315 -109.4
80 6 0 5 0 1.2 0.232 0.315 43.76
Total σq for point A = 172.8 – 109.4 + 43.76 = 107.16 kPa
45

46. Point B
Load(kPa) z r a r/a z/a A B σq=Q(A+B)
200 6 5 10 0.5 0.6 0.428 0.378 161.2
-200 6 5 5 1 1.2 0.151 0.149 -60
80 6 5 5 1 1.2 0.151 0.149 24
Total σq for point B = 161.2 – 60 + 24 = 125.2 kPa
46

47. Point C
Load(kPa) z r a r/a z/a A B σq=Q(A+B)
200 6 10 10 1 0.6 0.256 0.144 80
-200 6 10 5 2 1.2 0.053 0.000 -10.6
80 6 10 5 2 1.2 0.053 0.000 4.24
Total σq for point C =80 – 10.6 + 4.24 = 73.64 kPa
47

48. Figure Q1(a) shows the plan view of a circular raft foundation with the outer
diameter 30 m and the inner circular diameter of 15 m. The foundation
founded at 2 m depth below the ground surface. The shaded area carries a
uniformly distributed load of 250 kPa and the un-shaded annular area
carries a uniformly distributed load of 100 kPa. Using the factors given in
Appendix 1, calculate the increase in vertical stresses, ∆σz at 5.0 m below
ground surface at point A, B and C. Point A is located at a centre of
foundation, point B at outer annular diameter and point C at a distance as
stated in the figure.
48
EXAMPLE 5.2

49. Depth, z = 5 – 2 = 3
Section
un-shaded area shaded area un-shaded
area
(1) (2) (3)
Uniform
Contact
pressure, q
100 kPa 250 kPa 100 kPa
a 30 = 15
2
15 = 7.5
2
15 = 7.5
2
+ -
49

50. At point A, (r = 0 m)
Section r/a z/a
Ic
( A + B)
∆σz = q Ic
(kPa)
(1) 0 / 15 = 0 3 / 15 =
0.2
0.804 +
0.188
= 0.992
100( 0.992)
=99.2
(2) 0 / 7.5 = 0 3 / 7.5 =
0.4
0.629 +
0.320
= 0.949
250( 0.949)
=237.25
(3) 0 / 7.5 = 0 3 / 7.5 =
0.4
0.629 +
0.320
= 0.949
100(0.949)
=94.9
Σ∆σz 241.55 kPa
50

51. At point B, (r = 15 m)
Section r/a z/a Ic( A + B)
∆σz = qIc
(kPa)
(1) 15 / 15 =
1
3 / 15 =
0.2
0.383 + 0.085
=0.468
100( 0.468)
= 46.8
(2) 15 / 7.5 =
2
3 / 7.5 =
0.4
0.031 +(-0.025)
=0.006
250( 0.006)
= 1.5
(3) 15 / 7.5 =
2
3 / 7.5 =
0.4
0.031 +(-0.025)
=0.006
100(0.006)
= 0.6
Σ∆σz 47.7 kPa
51

52. At point C, ( r = √(202 + 302 ) = 36.06m )
Section r/a z/a
Ic( A + B) ∆σz = q
Ic(kPa)
(1) 36.06 / 15
= 2.4
3 / 15 =
0.2
0.0118 +
(-0.0112)
= 0.0006
100
(0.0006)
= 0.06
(2) 36.06 / 7.5
= 4.8
3 / 7.5 =
0.4
0 0
(3) 36.06 / 7.5
= 4.8
3 / 7.5 =
0.4
0 0
Σ∆σz 0.06kPa
52

53. ⚫ Most widely used in soil
engineering design.
⚫ Component stress can be
obtained by integrating the
Boussinesq expressions
2.6 Stresses Due to a Uniformly Loaded
Rectangular Area L
B
z
z = q IR
E6. Worked example 6.5 --- Page 200 (Text book)
53

54. Uniform Load On Rectangular Area
⚫ Vertical pressure determined utilizing influence
coefficient table 6-2, page 161
⚫ Where:
(z) = depth below loaded surface
⚫ Load is acting on area of rectangle:
(B) = width of rectangle
(L) = length of rectangle
54

55. To Calculate Vertical Pressure Below A
Uniform Load On Rectangular Area
⚫ First:
– Compute ratios (n = B/z) & (m = L/z,)
⚫ Then:
– determine Influence coefficient from table 6-2
⚫ Either:
– (n or m) can be read along first column
– Then other (m or n) across top
⚫ Then find vertical increment stress (p):
(p) = Influence coefficient x uniform Load
55

56. Either (n) or (m) can be read along
first column & The other (n or m) is read across top
56

57. Uniform Load On Rectangular Area
⚫ Influence Coefficient can also be
determined per
⚫ figure 6-8, page 162
⚫ Then:
– Influence coefficient is multiplied
by uniform load
– To determine pressure at depth (z)
below each corner of rectangle
57

58. Example 6.1
Determine the stress increase in a point at a depth of 6 m below
a newly built spread footing, 3 m by 4 m in area, placed on the
ground surface with a columnar axial load of N = 1800 kN.
Reduced parameters for the shaded area:
B1 = 1.50 m and L1 = 2.00 m
m1 = B1 / Z = 1.50/ 6.00 = 0.25
n1 = L 1/ Z = 2.00 / 6.00 = 0.33
qo= 1800 / 3*4= 150 kN
I R = 0.0344
σ q = qo (4 I R) = 1800/12
(4)(0.344)
σq = 20.7 kPa
58

59. Uniform Load On Rectangular Area
(Other than point directly below corner)
⚫ Accomplished by:
– Dividing area into rectangles
– Each having one corner directly above the point at which
the pressure is desired at depth (z)
– Pressure is computed for each rectangle
– Results are added or subtracted to get total pressure
59

60. Combination of Rectangles
used to obtain stress below a Specific point
60

61. Uniform Load On A Strip Area
⚫ Vertical pressure below uniform
load on a Strip area
⚫ Determined by:
– Utilizing figure 6-14
– (similar to figure 6-6) for loaded
circular area
⚫ With the exception:
– B = width
– R = radial horizontal distance from
strip footing’s center line
– z = depth
61

62. EXAMPLE 6.2
A
A B
C D
0.6 m
0.6 m
3.0 m
1.5 m
G
3.0 m
q = 80 kN/m2
G
FIGURE 1
62

63. Given:
Figure 1 shows a rectangular loaded area ABCD
The loaded exerted on the area is 80 kN/m2.
Required:
Vertical stress increment due to the exerted load at a depth
of 3.0 m below point G (FIGURE 1)
63

64. A
A
BC
D
3.0 m
SOLUTION:
F G
H
E
I
1. Extend the rectangular to the point G. (note: these three
areas share a common corner at point G)
64

65. 2. Then, compute ratios of
n = L/z m =B/z
Rectangle dimension m n Ir
DEGI 2.1 x 3.6 0.7 1.2 0.157
AEGH 3.6 X 0.6 0.2 1.2 0.057
CFGI 2.1 X 0.6 0.7 0.2 0.047
BFGH 0.6 X 0.6 0.2 0.2 0.018
Ir is obtained from FADUM’S CHART
65

66. Example 6.3
Find the influence factor from below FADUM’S CHART by
using value of m and n.
66

67. 4. Calculate the vertical stress due to increment under
point G.
= 0.157- 0.057-0.047+0.018
= 0.071
Hence ;
= 0.071 X 80
= 5.68 kN/m2
sI
qIsz =
=
)4321( IIII −−−
z
67

68. Figure below shows the plan of a rectangular foundation
which transmits a uniform contact pressure of 300kN/m2.
Determine the vertical stress induced by this loading.
a) at a depth of 4.58m below a
b) at a depth of 4.58m below b
Example 6.4
68

69. Point A Point B
69

70. At A
qo= Q = 300
A
M = b = 3.05 = 0.67
Z 4.58
N = L = 7.625 = 1.66
Z 4.58
From Fadum chart,
Ir = 0.16
σz = qo ( Ir1 + Ir2 + Ir3 + Ir4 )
= qo ( 4Ir1)
= 300 ( 4 X 0.16)
= 192kPa
At B
qo= Q = 300
A
M = b = 6.1 = 1.33
Z 4.58
N = L = 7.625 = 1.66
Z 4.58
From Fadum chart,
Ir = 0.21
σz = qo ( Ir1 + Ir2 )
= qo ( 2Ir1)
= 300 ( 2 X 0.21)
= 126kPa
Solution:
70

71. Take note that the
values of m ( =L/z) and
n ( =B/z) are
interchangeable !!
Fadum’s Chart
71

72. EXAMPLE 6.5
72

73. Solution
∆σZA= ∆σZ(1) + ∆σZ(2) - ∆σZ(3) -∆σZ(4)
1.5 m
0.75 0.75
1 m
A
2m 1 2
3 4
73

74. 74

75. Rectangle z = 2m
m = B/Z n = L /Z IR
1 2/2 0.75/2 0.1
3 1/2 0.75/2 0.07
2 2/2 0.75/2 0.1
4 1/2 0.75/2 0.07
= qIR(1) + qIR(2) -qIR(3) -qIR(4)
q = 550/ ( 1 x 1.5 )
= 366.67 kPa
∆σZA = 366.67 (0.1+0.1-0.07-0.07)
= 22 kPa
75

76. 76

77. Figure shows the plan of a rectangular raft foundation which transmits a
uniform contact pressure of 180kPa to the soil beneath. The line of a
culvert is also shown, which passes under the raft at a depth to the soft of
3m (fall ignored). Calculate the intensity of vertical stress on the culvert that
will be induced by the raft loading at the points A, B, C, D and E shown.
A
B
C
D
E
2.5 m
2.0 m
2.0 m
2.0 m
2.0 m
8.0 m
15.0 m
A
B
EXAMPLE 6.6
77

78. A
1
2
3
4
Z=3.0m
4.0m
4.0m
7.5m 7.5m
1. B/Z = 1.33 L/Z= 2.5 IR1= 0.22
2. B/Z = 1.33 L/Z= 2.5 IR2= 0.22
3. B/Z = 1.33 L/Z= 2.5 IR3= 0.22
4. B/Z = 1.33 L/Z= 2.5 IR4= 0.22
∆Бz = q0 (IR1 + IR2 + IR3 + IR4)
= 180 (0.22 + 0.22 + 0.22 + 0.22)
= 158.4 KN/m²
q0 = 180 Kpa
78

79. 1 2
34
Z=3.0m
2.0m
6.0m
10m 5.0m
1. B/Z = 0.67 L/Z= 3.33 IR1= 0.17
2. B/Z = 0.67 L/Z= 1.67 IR2= 0.16
3. B/Z = 1.67 L/Z= 2.0 IR3= 0.225
4. B/Z = 2.0 L/Z= 3.33 IR4= 0.23
∆Бz = q0 (IR1 + IR2 + IR3 + IR4)
= 180 (0.17 + 0.16 + 0.225 + 0.23)
= 141.3 KN/m²
q0 = 180 Kpa
B
79

80. 1 2
Z=3.0m
8.0m
12.5m 2.5m
1. B/Z = 2.67 L/Z= 4.17 IR1= 0.25
2. B/Z = 0.83 L/Z= 2.67 IR2= 0.19
∆Бz = q0 (IR1 + IR2)
= 180 (0.25 + 0.19)
= 79.2 KN/m²
q0 = 180 Kpa
c
80

81. 1
2
Z=3.0m
2.0m
8.0m
15m
1. B/Z = 0.67 L/Z= 5.0 IR1= 0.17
2. B/Z = 2.67 L/Z= 5.0 IR2= 0.25
∆Бz = q0 (IR1 - IR2)
= 180 (0.25 - 0.17)
= 14.4 KN/m²
q0 = 180 Kpa
D
81

82. 1 2
34
Z=3.0m
4.0m
8.0m
15m
1. B/Z = 2.67 L/Z= 5.0 IR1= 0.25
2. B/Z = 0.83 L/Z= 4.0 IR2= 0.19
3. B/Z = 0.83 L/Z= 1.33 IR3= 0.185
4. B/Z = 1.33 L/Z= 5.83 IR4= 0.215
∆Бz = q0 (IR1 - IR2 – IR4 + IR3)
= 180 (0.25 – 0.19 – 0.215 + 0.185)
= 5.4 KN/m²
q0 = 180 Kpa
E
2.5m
82

83. Figure shows the layout plan of four 3mX3m
square foundations carrying uniform load of 150
kpa each. Determine the vertical stress increase
induced by these foundations in the soil at the
depth of 3 m below point A
EXAMPLE 6.7
83

84. 150 kPa 150 kPa
150 kPa 150 kPa
3 m 3 m 3 m
3 m
3 m
3 m
A
84

85. 150 kPa 150 kPa
150 kPa 150 kPa
3 m 3 m 3 m
3 m
3 m
3 m
A
3 m
85

86. A
1.5m
1.5m
3m
3m
86

87. Bil Area
(m)
x
(m)
y
(m)
z
(m)
m = x/z
(m)
n = y/z
(m)
Ip qо
(kN)
σz = qо.I
(kPa)
1 20.25 4.5 4.5 3 1.5 1.5 0.215 150 32.25
2 9.00 3 3 3 1.0 1.0 0.191 150 28.65
3 6.75 1.5 4.5 3 0.5 1.5 0.130 150 -19.50
4 2.25 1.5 1.5 3 0.5 0.5 0.130 150 19.50
∑ 70.50
Vertical stress, Δσz = 70.5 X 4
= 283.6 kPa
Vertical stress, σz = P . Ip
z²
= 4726.7 kPa
87

88. 10 m
10 m
An L-shaped raft foundation is to carry superstructure loads
with net loading intensity of 600kN/m2 and 1200kN/m2 as
shown in figure. Using Fadum’s chart, determine the net
increase in vertical stress 4m below points A and B.
Note : A = centre of the square
B = mid-point of the side
30 m
30 m
600kPa
1200kPa
A B
EXAMPLE 6.8
88

89. At Point A
Σσz = Σσz1 + Σσz2
600kPa
+
IR1 IR2
IR3
IR4
IR5
IR7
600kPa
IR6
89

90. Rectangular z = 4m
m= B/z n= L/z IR (kPa)
1 5/4 = 1.25 25/4 =6.25 0.215
2 5/4 = 1.25 25/4 =6.25 0.215
3 5/4 = 1.25 25/4 =6.25 0.215
4 5/4 = 1.25 25/4 =6.25 0.215
5 5/4 = 1.25 5/4 = 1.25 0.190
6 5/4 = 1.25 5/4 = 1.25 0.190
7 5/4 = 1.25 5/4 = 1.25 0.190
90

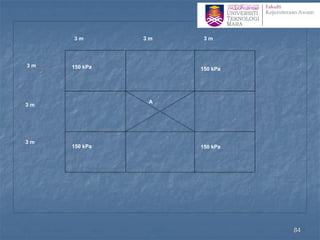
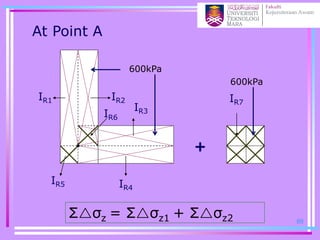
91. Σσz = Σσz1 + Σσz2
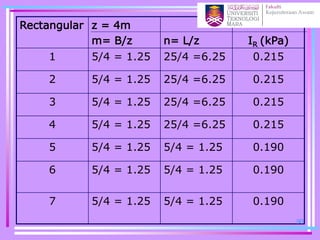
= q(IR1+IR2+IR3+IR4+IR5- IR6)
+q(4IR7)
= 600[4(0.125) + 0.190 - 0.910]
+ 600[4(0.190)]
= 516 + 456
= 972kPa
91

92. At Point B
+
IR1
IR3
IR4IR2
IR5
Σσz = Σσz1 + Σσz2
600kPa
600kPa
92

93. Rectangular z = 4m
m= B/z
n= L/z IR
1 10/4 = 2.5 25/4 =6.25 0.245
2 5/4 = 1.25 10/4 = 2.5 0.215
3 5/4 = 1.25 20/4 = 5 0.208
4 5/4 = 1.25 20/4 = 5 0.208
5 5/4 = 1.25 10/4 = 2.5 0.215
93

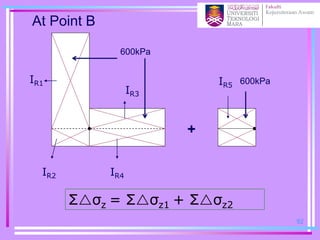
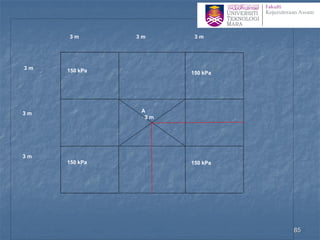
94. Σσz = Σσz1 + Σσz2
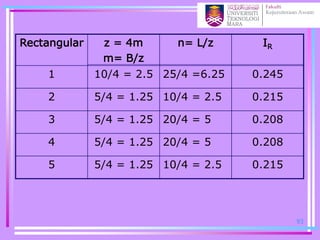
= q(IR1+IR2+IR3+IR4)+ q(2IR5)
= 600[0.245+0.215+2(0.208)]
+ 600[2(0.215)]
= 525.6 + 258
= 783.6kPa
94

95. Determination of stress below an arbitrary shape
Newmark’s Chart
1. The scale for this procedure is determined by the depth z at
which the stress is to be evaluated, thus z is equal to the distance
OQ shown on the chart.
95

96. O Q
z
z
96

97. Determination of stress below an arbitrary shape
Newmark’s Chart
1. The scale for this procedure is determined by the depth z at
which the stress is to be evaluated, thus z is equal to the distance
OQ shown on the chart.
2. Draw the loaded area to scale so that the point of interest
(more correctly its vertical projection on the surface) is at the
origin of the chart, the orientation of the drawing does not
matter
97

98. O Q
z
z
98

99. Determination of stress below an arbitrary shape
Newmark’s Chart
1. The scale for this procedure is determined by the depth z at
which the stress is to be evaluated, thus z is equal to the distance
OQ shown on the chart.
2. Draw the loaded area to scale so that the point of interest
(more correctly its vertical projection on the surface) is at the
origin of the chart, the orientation of the drawing does not
matter
3. Count the number of squares (N) within the loaded area, if
more than half the square is in count the square otherwise
neglect it.
99

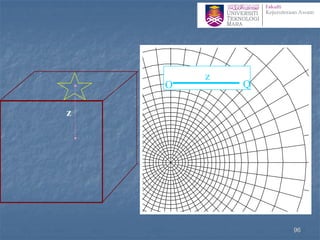
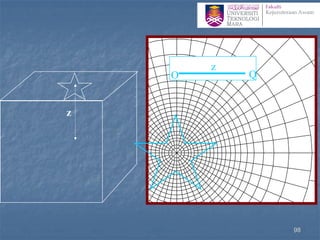
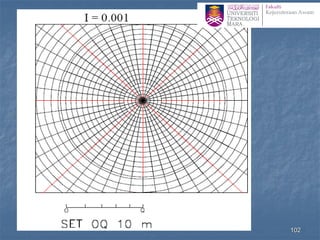
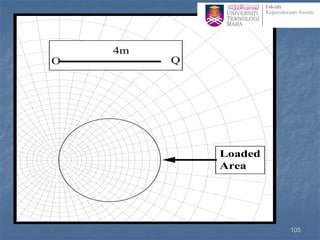
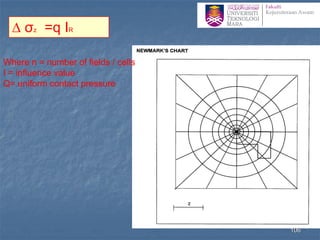
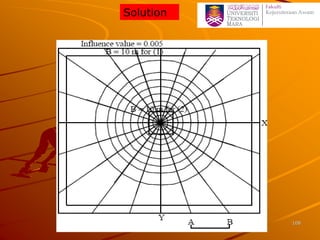
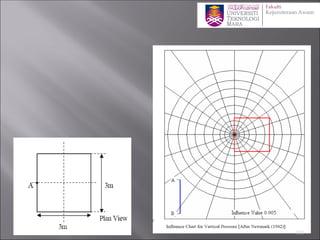
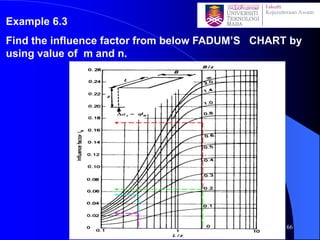
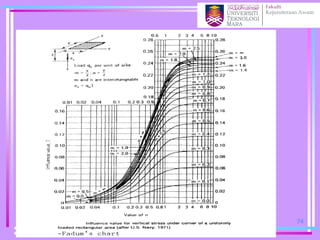
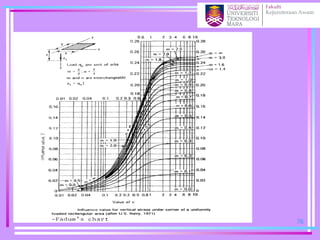
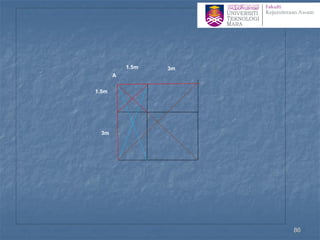
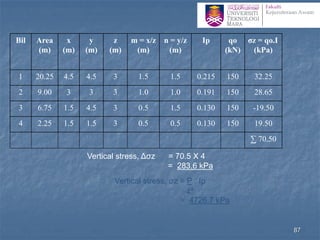
100. Determination of stress below an arbitrary shape
Newmark’s Chart
1. The scale for this procedure is determined by the depth z at
which the stress is to be evaluated, thus z is equal to the distance
OQ shown on the chart.
2. Draw the loaded area to scale so that the point of interest
(more correctly its vertical projection on the surface) is at the
origin of the chart, the orientation of the drawing does not
matter
3. Count the number of squares (N) within the loaded area, if
more than half the square is in count the square otherwise
neglect it.
4. The vertical stress increase zz= N ´ [scale factor(0.001)] ´
[surface stress (p)] 100

101. A circular oil storage tank will be built at the shore of
Tampa Bay. It will be 20 m in diameter, and 15 m high.
The tank sits upon a 2 m thick sand deposit that rests
upon a clay stratum 16 m thick. The water table is at
practically at the surface. Find the stress increase from
a fully loadedtank,
1- at mid-clay stratum, (a) directly under the center of
the tank,
2- at its outer edge, using the Newmark influence chart
shown below.
IR= 0.001
EXAMPLE 6.9
101

102. 102

103. The contact stress is qo = goil h = (0.95)(9.81 kN/m3)(15m) = 140 kN/m2
At mid-clay depth along the centerline of the tank (depth = 10m)
OQ = 10 m
IV = 0.001 and N = 648
Therefore v’ = (qo - gwh) (IV)N = (140 - 9.81 x 10)(0.001)(648) = 27 kN/m2
103

104. Suppose a uniformly loaded circle of radius 2 m carries a uniform stress
of 100 kPa. It is required to calculate the vertical stress at a depth of 4 m
below the edge of the circle.
Solution
The loaded area is drawn on Newmark’s chart to the appropriate scale
(i.e. the length OQ is set to represent 4 m) as shown in below.
It is found that the number of squares, N = 194 and so the stress
increase is found to be
zz = 194  0.001  100 = 19.4 kPa
104

105. O Q
4m
Loaded
Area
105

106. ∆ σz =q IR
Where n = number of fields / cells
I = influence value
Q= uniform contact pressure
106

107. A construction project site has a surface layer of sand, 2
m thick, underlain by a 10 m thick clay stratum. The
project involves placing a wastewater treatment tank, 10
m square, with a contact pressure qo of 400 kN/m2.
Find the stress at mid-tank, at the top and the bottom of
the clay stratum, using Newmark’s influence chart,
shown below
EXAMPLE 2.10
107

108. Solution
108

109. For p1, AB = 2m. Therefore:
p1 = (IV) qo N = (0.005)(400 kN/m2)(190)
p1 = 380 kN/m2
For p2, AB = 2m. Therefore:
p2 = (0.005)(400 kN/m2)(42)
p2 = 84 kN/m2
109

110. Find the stress at the point A shown below, at a depth of 3 m below the
edge of the footing. The plan of the square footing has been plotted on top
of the Newmark graph to a scale of AB = 3m and placed in such a way
that point A falls directly over the center of the chart.
EXAMPLE 6.11
110

111. 111

112. 112

113. Pressure bulbs for vertical stress
(a) Circular foundation
(b) Strip foundation
2 or 4B
B
2 or 4B
B
113

114. Pressure bulbs indicating depth to which soil is significantly
stressed
114