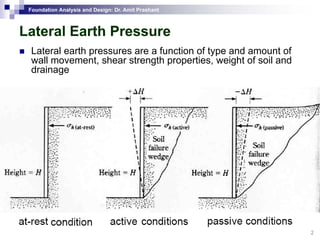
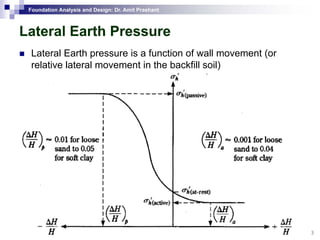
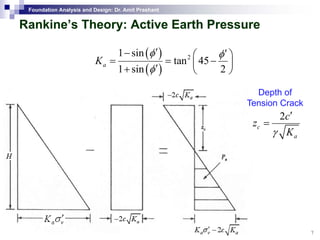
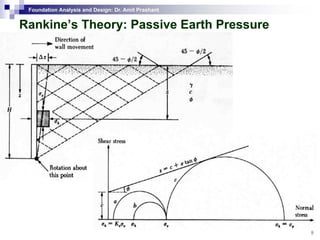
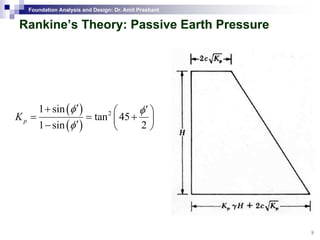
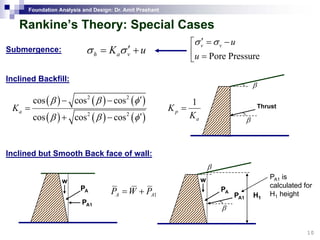
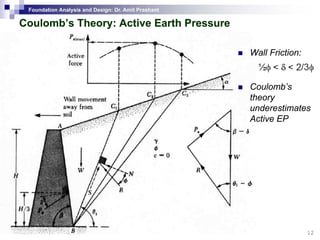
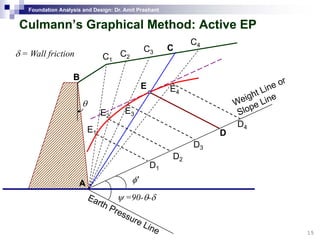
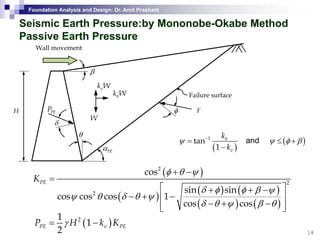
This document discusses lateral earth pressure and methods for calculating active and passive earth pressures on retaining walls. It introduces the concepts of earth pressure at rest, Rankine's theory, and Coulomb's theory for calculating lateral earth pressures. It also describes the Mononobe-Okabe method for calculating seismic earth pressures as a function of factors like soil properties, wall geometry, and ground acceleration. Graphical methods like Culmann's method are also presented for determining active and passive earth pressures.

1. CE-632
Foundation Analysis and
DesignDesign
Lateral Earth PressureLateral Earth PressureLateral Earth PressureLateral Earth Pressure
1

2. Foundation Analysis and Design: Dr. Amit Prashant
Lateral Earth PressureLateral Earth PressureLateral Earth PressureLateral Earth Pressure
Lateral earth pressures are a function of type and amount of
wall movement shear strength properties weight of soil andwall movement, shear strength properties, weight of soil and
drainage
2

3. Foundation Analysis and Design: Dr. Amit Prashant
Lateral Earth PressureLateral Earth PressureLateral Earth PressureLateral Earth Pressure
Lateral Earth pressure is a function of wall movement (or
relative lateral movement in the backfill soil)
3

4. Foundation Analysis and Design: Dr. Amit Prashant
Lateral Earth Pressure at RestLateral Earth Pressure at Rest
Coefficient of earth pressure at rest, o h vK σ σ′ ′=
(No Lateral Movement)
p ,
The vertical al stress at any depth, z, is:
o h v
v q zσ γ′ ′= +
K′ ′ + u = pore water pressureh o vK uσ σ= + u = pore water pressure
Elastic Solution:
1
oK
ν
ν
=
−
Poisson’s
ratio
4

5. Foundation Analysis and Design: Dr. Amit Prashant
Coefficient of Earth Pressure at RestCoefficient of Earth Pressure at RestCoefficient of Earth Pressure at RestCoefficient of Earth Pressure at Rest
For coarse-grained soils (Jaky 1944)For coarse grained soils (Jaky, 1944)
K0 = 1 – sin φ’
For fine-grained normally consolidated soils (Massarch 1979)For fine grained, normally consolidated soils (Massarch, 1979)
⎥
⎦
⎤
⎢
⎣
⎡
+=
100
(%)
42.044.0
PI
Ko
Brooker and Ireland, 1965
K0 = 0.95 – sin φ’
⎦⎣ 100
0 φ
For overconsolidates clays
OCRKK COC )()( = cP
OCR =
Mayne and Kulway, 1982
K0 = (1 – sin φ’).OCRsin φ’
OCRKK NCoOCo )()( =
o
OCR
'σ
5
K0 (1 sin φ ).OCR

6. Foundation Analysis and Design: Dr. Amit Prashant
Rankine’sRankine’s Theory: Active Earth PressureTheory: Active Earth Pressureyy
6

7. Foundation Analysis and Design: Dr. Amit Prashant
Rankine’sRankine’s Theory: Active Earth PressureTheory: Active Earth Pressureyy
( ) 21 sin
tan 45K
φ φ′− ′⎛ ⎞
⎜ ⎟
( )
( )
tan 45
1 sin 2
aK
φ
= = −⎜ ⎟′+ ⎝ ⎠
D th f
2c′
Depth of
Tension Crack
c
a
z
Kγ
=
7

8. Foundation Analysis and Design: Dr. Amit Prashant
Rankine’sRankine’s Theory: Passive Earth PressureTheory: Passive Earth Pressureyy
8

9. Foundation Analysis and Design: Dr. Amit Prashant
Rankine’sRankine’s Theory: Passive Earth PressureTheory: Passive Earth Pressureyy
( )
( )
21 sin
tan 45K
φ φ′+ ′⎛ ⎞
= = +⎜ ⎟
⎝ ⎠( )
tan 45
1 sin 2
pK
φ
+⎜ ⎟′− ⎝ ⎠
9

10. Foundation Analysis and Design: Dr. Amit Prashant
Rankine’sRankine’s Theory: Special CasesTheory: Special Casesy py p
Submergence:
h a vK uσ σ′= +
Pore Pressure
v v u
u
σ σ′ = −⎡
⎢
=⎣⎣
Inclined Backfill:
β
( ) ( ) ( )
( ) ( ) ( )
2 2
2 2
cos cos cos
cos cos cos
aK
β β φ
β β φ
′− −
=
′+ −
1
p
a
K
K
= Thrust
β( ) ( ) ( )cos cos cosβ β φ+ a β
Inclined but Smooth Back face of wall:
w
β
w PA1 is
w
PA1
PA
1A AP W P= +
w
PA1
PA
β
H1
A1
calculated for
H1 height
10
β

11. Foundation Analysis and Design: Dr. Amit Prashant
Rankine’s Theory: Special CasesRankine’s Theory: Special CasesRankine’s Theory: Special CasesRankine’s Theory: Special Cases
β
Inclined Backfill with c‘ φ‘ soil:
Thrust
β
Inclined Backfill with c -φ soil:
⎧ ⎫′⎛ ⎞
β
2
2 2
2cos 2 cos sin
1
1
cos
a
c
z
K
β φ φ
γ
φ
⎧ ⎫′⎛ ⎞
′ ′+⎪ ⎪⎜ ⎟
⎝ ⎠⎪ ⎪
= −⎨ ⎬
′ ′ ′⎛ ⎞ ⎛ ⎞⎪ ⎪
( )2 2 2 2 2
cos
4cos cos cos 4 cos 8 cos cos sin
c c
z z
φ
β β φ φ β φ φ
γ γ
′ ′⎛ ⎞ ⎛ ⎞⎪ ⎪
′ ′ ′ ′− − + +⎜ ⎟ ⎜ ⎟⎪ ⎪
⎝ ⎠ ⎝ ⎠⎩ ⎭
2
2
2cos 2 cos sin
1
1
c
z
K
β φ φ
γ
⎧ ⎫′⎛ ⎞
′ ′+⎪ ⎪⎜ ⎟
⎝ ⎠⎪ ⎪
= −⎨ ⎬
( )
2 2
2 2 2 2 2
1
cos
4cos cos cos 4 cos 8 cos cos sin
pK
c c
z z
φ
β β φ φ β φ φ
γ γ
⎨ ⎬
′ ′ ′⎛ ⎞ ⎛ ⎞⎪ ⎪
′ ′ ′ ′+ − + +⎜ ⎟ ⎜ ⎟⎪ ⎪
⎝ ⎠ ⎝ ⎠⎩ ⎭ 11

12. Foundation Analysis and Design: Dr. Amit Prashant
Coulomb’s Theory: Active Earth PressureCoulomb’s Theory: Active Earth Pressure
Wall Friction:
Coulomb’s
theory
underestimates
Active EPActive EP
12

13. Foundation Analysis and Design: Dr. Amit Prashant
Coulomb’s Theory: Passive Earth PressureCoulomb’s Theory: Passive Earth Pressure
Wall Friction:
Coulomb’s
theory
overestimates
Passive EPPassive EP
13

14. Foundation Analysis and Design: Dr. Amit Prashant
Coulomb’s Theory: SolutionsCoulomb’s Theory: Solutionsyy
14

15. Foundation Analysis and Design: Dr. Amit Prashant
Culmann’sCulmann’s Graphical Method: Active EPGraphical Method: Active EPpp
δ = Wall friction C1
C2
C3
C4
C
B
1
E4
E
θ
E2
E3
E4
E1
D3
D4
D
φ'A
D1
D2
φ
ψ =90-θ-δ
A
15

16. Foundation Analysis and Design: Dr. Amit Prashant
Culmann’sCulmann’s Graphical Method: Passive EPGraphical Method: Passive EPpp
δ = Wall friction C1
C2
C3
C4
C
E1
f
B
C1
2
E2
E3
E4
E
θ
4
A φ'
ψ
=90 θ+δ
Ea
Pres
Lin
A
D1
D2
φ'
16
=90-θ+δ
rth
sure
ne
D3
D4
D

17. Foundation Analysis and Design: Dr. Amit Prashant
Seismic EarthSeismic Earth Pressure:byPressure:by MononobeMononobe--Okabe MethodOkabe Method
Active Earth PressureActive Earth Pressure
Wall movement : angle of internal friction of soil
θ b tt l f ll
vk W
β
θ: batter angle of wall
δ: angle of friction between the
wall and the backfill
hk W
W φ
Failure surface
H
wall and the backfill
β: slope of the backfill top
surfaceW φ
α
θ
AEP
δ
F
( )
1
tan
1
h
v
k
k
ψ −
=
−
and ( )ψ φ β≤ −
AEα
( )2
cos
K
φ θ ψ− −
=
( )
( )
( ) ( )
( ) ( )
2
2 sin sin
cos cos cos 1
cos cos
AEK
δ φ φ β ψ
ψ θ δ θ ψ
δ θ ψ β θ
=
⎡ ⎤+ − −
+ + +⎢ ⎥
+ + −⎢ ⎥⎣ ⎦
17
⎣ ⎦
( )21
1
2
AE v AEP H k Kγ= − Assumed to be acting at H/2.

18. Foundation Analysis and Design: Dr. Amit Prashant
Seismic EarthSeismic Earth Pressure:byPressure:by MononobeMononobe--Okabe MethodOkabe Method
Passive Earth PressurePassive Earth Pressure
Wall movement
vk W
β
hk W
v
W
φPEP F
Failure surface
H
W
PEα
θ
δ
( )
1
tan
1
h
v
k
k
ψ −
=
−
( )ψ φ β≤ +and
PEα
( )2
cos
K
φ θ ψ+ −
=
( )v
( )
( ) ( )
( ) ( )
2
2 sin sin
cos cos cos 1
cos cos
PEK
δ φ φ β ψ
ψ θ δ θ ψ
δ θ ψ β θ
=
⎡ ⎤+ + −
− + −⎢ ⎥
− + −⎢ ⎥⎣ ⎦
18
⎣ ⎦
( )21
1
2
PE v PEP H k Kγ= −